Trie树入门

Trie树入门

貌似很多人会认为\(Trie\)是字符串类型，但是这是数据结构！！！。

详情见度娘

下面开始进入正题。

PS:本文章所有代码未经编译，有错误还请大家指出。

引入

先来看一个问题

​ 给定一本字典中的\(n\)个单词，还有\(m\)个询问。每次询问询问一个单词是否出现在这\(n\)个单词中。

暴力

最简单的就是暴力做法啦,我们直接枚举去判别对应位置,还可以再加点优化。

即：长度不同，肯定不是同一个单词。

for(int l;m;m--)
{
    bool flg=false;
    scanf("%s",str);
    l=strlen(str);
    for(int i=1;i<=n;i++)
    {
        int len=strlen(s[i])
        if(l!=len)continue;
        for(int j=1;j<=len;j++)
        {
            if(s[i][j]!=str[j])
            {
                flg=true;
                break;
            }
        }
        if(flg)
        {
            for(int j=1;j<=len;j++)
                printf("%c",s[i][j]);
		}
        putchar('\n');
	}
}

时间复杂度为\(O(n\times m\times len)\)

加强

很容易发现暴力不是很好写。而且数据范围再大一点的话就根本跑不动，而且存不下。

当数据范围加强到刚刚好直接存储,存储不下的时候。我们就要考虑改进。

那么如何改进呢？

深入

假如给定我们的\(n\)个单词是这样的。

\[abcaa\\aabca\\abdac\\aabcabd\\bacabd\\ \dots
\]

那么我们考虑这样一个问题

Q:空间浪费在了哪里？

A:容易发现的是，在保证单词不乱序的情况下，他们的部分前缀是相同的！那么我们是不是可以从这里入手来减少空间复杂度呢？

当然可以啊！这个时候我们需要联想到树的性质：

1. 相同的可以压缩成一个节点(那我们就能将这些前缀压缩来减少空间消耗)
2. 树上路径唯一。(那我们就可以保证每一个单词之间的存储互不影响)

由此，我们便引出了\(Trie\)树

浅谈Trie树

简介

​ Trie是一种多叉树，在对单词处理中是经常利用的一种数据结构，是树结构中一种较为特殊的树结构，它在计算机中对字符采用链表方式存储 。

​ ---百度百科

基本性质

Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。

它有3个基本性质：

1. 根节点不包含字符，除根节点外每一个节点都只包含一个字符。

2. 从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。

3. 每个节点的所有子节点包含的字符都不相同。

   ​ ---百度百科

形态

一般的Trie有两种存储方式：

1. 将字符存储在边上
2. 将字符存储在点上

这里给出将字符存储在点上的形式

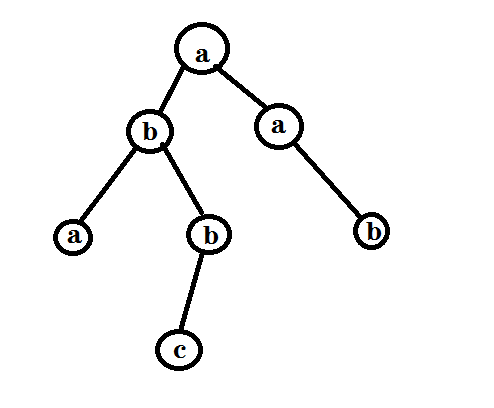
大概就是这个样子啦。

这样从根节点到任何一个子节点就都是一个存储的单词啦。

图中所存储的就是这些单词咯

\[aba\\abbc\\aab
\]

(由于时间问题就没有作一颗比较大的Trie，见谅。)

构建

知道了\(Trie\)的一些简单东西。

那么我们考虑如何构建一棵\(Tire\)。

显然我们需要将一个单词完整存储就需要遍历整个单词来存储每一位字母。

并且我们需要从浅入深地遍历这棵树。

写法可以为递归版本，也可以为非递归版本。

这里给出非递归版本。

code

void ins(char *s)
{
    int rt=0;
    for(int i=0,v;s[i];i++)
    {
       int v=s[i]-'a';
        if(!trie[rt][v])
            trie[rt][v]=++tot;//给每个节点一个编号,tot为全局变量
        rt=trie[rt][v];//向下一个节点,继续存储当前单词
	}
}

由我们构建函数可知，Trie的空间复杂度为(单词长度 \(\times\) 字符种类 )。

且这个构建过程的时间复杂度为\(O(n^2)\)

时间复杂度证明,不会 emmm。

查询操作

Trie树一般支持两种查询操作：

1. 查询单词是否出现过。
2. 查询单词的出现次数。

有些时候，根据写法的不同，我们还可以判断一个单词是不是某个单词的前缀。

当然如果你构建后缀的Trie的话，还可以判断这个单词是不是某个单词的后缀。而这个树又名为后缀树。

对于后缀树这里不进行研究。(等我有时间会写的。)

不论是哪种查询操作，我们都需要遍历整棵树来判断是否存在这些节点。

依旧有两种写法，这里给出非递归版。

code

bool find(char *s)
{
    int rt=0;
    for(int i=0,v;s[i];i++)
    {
        v=s[i]-'a';
        if(!trie[rt][v])retturn false;
        rt=trie[rt][v];
	}
    if(ok[rt])return true;
    //加上这一句可以判断当前单词是否出现过。
    //而如果不加，就可以判断当前单词是不是某个单词的前缀
    //如果加上这一句的话就在构建的时候对应的在词尾标记即可。
    return false;
}

根据\(m\)个询问，再进行遍历，显然这样的时间复杂度为\(O(n^2)\)。

而Trie的应用还有很多。这里不一一介绍了，毕竟我是个退役选手啊。

具体的完整代码详见例题部分。

后面继续深入学习的话还有01Trie，可持久化Trie.

下面讲解一下01Trie

01Trie

有一类问题叫做01字典树问题，它是用来解决xor的有力武器，通常是给你一个数组，问你一段连续的异或和最大是多少，正常思路贪心dp啥的都会一头雾水，但是用01字典树就能很快的解决，实现起来也十分方便(其实和trie树差不多。

实现

01字典树的实现可以看成是把一个数的二进制字符化后插入到一棵一般的字典树中。

那你们会不会有疑问就是说 当某一个数的二进制位是另一个数的二进制位的某一前缀的时候 是不是查不到这个数

\[7 =111_{(2)} \\3=11_{(2)}
\]

然后这个时候 我们可以做一个处理 即 从一个特别特别长的位置开始插入(一般会选择 1<<30位开始处理 ，对应：01字典树种插入3时 相当于在字典树中插入00 …..00011)

但还是要见题而异

操作

当我们查询最大异或值的时候，我们从最高位向下贪心查找。

贪心策略：

当前查找第k位,二进制数位x,如果存在x^1的节点,我们就进入这个节点,否则进入x节点。

证明：

这个不太会用文字来叙述，直接看一下比较。

\[8=1000_{(2)}\\7=0111_{(2)}
\]

很明显，当前对应的最高位上是\(1\)，比它后面位上全是\(1\)要大。

因此我们的策略是正确的。

性质

对应01Trie的性质与Trie的相似，这里不再赘述。

而我们引入一个重要的性质：

如果要求[l,r]的异或和:

由\(X \ xor \ X = 0;0 \ xor\ Y = Y；\)

推知:所有\([l，r] = [1，r] XOR[1，l - 1]\)

构建

同样会有两种写法，这里给出非递归版本的代码

code

void ins(int x)
{
    int rt=0;
    for(int i=1<<30;i;i>>=1)
    {
        bool c=x&i;
        //这里推荐写bool类型，不推荐写int类型，因为很容易忘记是对应位为1
        if(!trie[rt][c])
            trie[rt][c]=++tot;//记录节点编号
        rt=trie[rt][c];
    }
}

应该不是很难理解，不作详细解释。

查询最大异或和

这里是查询一个数的最大异或和。

同样给出非递归版本的代码。

code

int query(int x)
{
    int ans=0,rt=0;
    for(int i=1<<30;i;i>>=1)
    {
        bool c=x&i;
        if(trie[rt][c^1])
            ans+=i,rt=trie[rt][c^1];
        //如果有我们就选择这个较高位来实现我们的贪心策略.记得累计答案
        else rt=trie[rt][c];
    }
    return ans;
}

小结

总的来说，在这有限的几个小时我也就只能写这么多吧。

再深入一些还是需要大家后期的学习。如果能帮助到大家很高兴。有不足之处还请大家多多指出。

例题

这些例题就不做深入剖析，有些我是写过题解的，都会给出链接。

如果觉得很麻烦就来我博客园链接好了.

Trie树

题目：TJOI2010 阅读理解 题解：这

题目：p2264 情书 题解：这

题目：UVA11362 Phone List 题解：这

01Trie

这些题目包括可持久化01Trie还有普通01Trie

题目：p4551 最长异或路径 题解：这

下面两个是可持久化01Trie

题目：TJOI2018 异或 题解：这

题目：p4735 最大异或和 题解：这

最后的话

感谢洛谷提供的题目。为洛谷打call！！

感谢百度百科提供的一些介绍。

原生态顾z创作。