P4491 [HAOI2018]染色 容斥+NTT

$ \color{#0066ff}{ 题目描述 }$

为了报答小 C 的苹果, 小 G 打算送给热爱美术的小 C 一块画布, 这块画布可 以抽象为一个长度为 \(N\) 的序列, 每个位置都可以被染成 \(M\) 种颜色中的某一种.

然而小 C 只关心序列的 \(N\) 个位置中出现次数恰好为 \(S\) 的颜色种数, 如果恰 好出现了 \(S\) 次的颜色有 \(K\) 种, 则小 C 会产生 \(W_k\) 的愉悦度.

小 C 希望知道对于所有可能的染色方案, 他能获得的愉悦度的和对 \(1004535809\) 取模的结果是多少.

\(\color{#0066ff}{输入格式}\)

从标准输入读入数据. 第一行三个整数 \(N, M, S\).

接下来一行 \(M + 1\) 个整数, 第 \(i\) 个数表示 \(W_{i-1}\) .

\(\color{#0066ff}{输出格式}\)

输出到标准输出中. 输出一个整数表示答案．

\(\color{#0066ff}{输入样例}\)

8 8 3
3999 8477 9694 8454 3308 8961 3018 2255 4910

55 96 4
396135414 150956526 115846323 684016411 478047433 741809293 841489850 30757425 354718 455244385 67265783 601148661 653297520 159551113 659259694 422602824 890944094 515558436 708977878 859628263 674258521 366153708 146971849 6161187 658301233 461136214 471709361 18786219 349277110 525215286 508995440 640141358 994347874 337617068 743448773 691546444 504640221 401810440 113565512 194628996 99765846 419008498 110931344 659189735 171012254 255189228 896007913 104632201 451664101 178069999 952991431 840513981 647057140 692809264 931718019 30010246 380306874 368517911 154597143 770763865 497641686 772741050 919136255 321190494 134863734 372165464 743950576 11194552 760810101 386902866 928594467 936096033 784108853 271133783 330481696 61402412 432546315 837809841 492881572 200968716 472860533 777800538 858285842 716767711 483244349 497540302 436003214 827152949 390815935 567741247 468900425 37709000 257282045 362991016 500424354 943931245 116395951

\(\color{#0066ff}{输出样例}\)

524070430

231524284

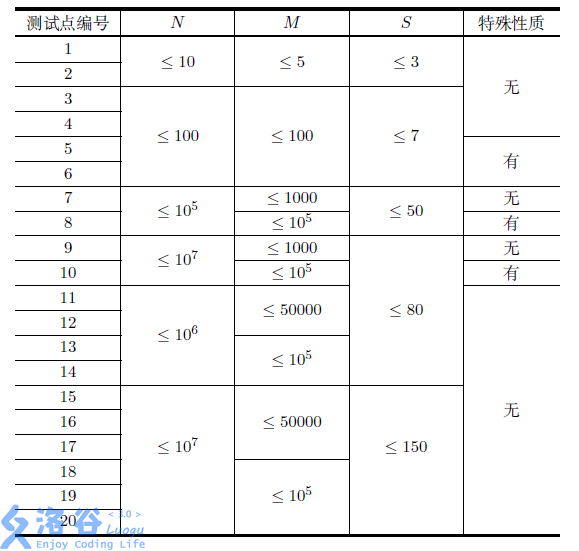
\(\color{#0066ff}{数据范围与提示}\)

特殊性质: \(\forall 1 \le i \le m, W_i = 0\)

对于 \(100\%\) 的数据, 满足 \(0 \le W_i < 1004535809\)

\(\color{#0066ff}{题解}\)

我们发现，如果钦定k种颜色出现S次，然后剩下位置的颜色选择肯定是m-k这些颜色，但是可能还会有颜色出现S次，我们并不能很容易的计算，于是考虑容斥

我们记一个\(f[i]\)表示出现S次的颜色\(\ge i\)种的方案数，这样设状态就可以不用管刚刚的问题了

然后我们考虑f的计算

首先，钦定i种颜色，组合数\(C_m^i\)，每种出现了S次，于是剩下的位置的个数就是\(n-iS\)

剩下的位置我们肯定是颜色随便选，注意不能选钦定的！所以方案显然是\((m-i)^{n-iS}\)

注意还有一部分贡献，就是颜色的位置！于是我们直接可重集排列一下，就是\(\frac{n!}{(S!)^i*(n-iS)!}\)

于是，我们f的计算方式就出来了\(f[i] = C_m^i*(m-i)^{n-iS}*\frac{n!}{(S!)^i*(n-iS)!}\)

然后我们计算答案，设\(ans[i]\)为出现S次颜色恰好i种的方案数，就是用f容斥一下

\(\begin{aligned}ans[i]=\sum_{j=i}^m(-1)^{j-i}*C_j^i*f[j]\end{aligned}\)

实际上并不用到m，可以发现，有贡献的最多同时存在的颜色种类数是\(min\{m, \frac n S\}\)

然后拆开组合数\(\begin{aligned}ans[i]=\sum_{j=i}^m(-1)^{j-i}*\frac{j!}{i!*(j-i)!}*f[j]\end{aligned}\)

然后稍微动一下，大致类似的放在一起\(\begin{aligned}ans[i]=\frac{1}{i!}\sum_{j=i}^m\frac{(-1)^{j-i}}{(j-i)!}*j!*f[j]\end{aligned}\)

显然这是个卷积的形式，直接翻转一下

\(\begin{aligned}ans[i]=\frac{1}{i!}\sum_{j=i}^m\frac{(-1)^{m-j+i+1}}{(m-j+i+1)!}*j!*f[j]\end{aligned}\)

然后NTT就行了。。

#include<bits/stdc++.h>
#define LL long long
LL in() {
	char ch; LL x = 0, f = 1;
	while(!isdigit(ch = getchar()))(ch == '-') && (f = -f);
	for(x = ch ^ 48; isdigit(ch = getchar()); x = (x << 1) + (x << 3) + (ch ^ 48));
	return x * f;
}
const int mod = 1004535809;
const int maxn = 1e7 + 100;
LL ksm(LL x, LL y) {
	LL re = 1LL;
	while(y) {
		if(y & 1) re = re * x % mod;
		x = x * x % mod;
		y >>= 1;
	}
	return re;
}
int len, r[maxn];
using std::vector;
void FNTT(vector<int> &A, int flag) {
	A.resize(len);
	for(int i = 0; i < len; i++) if(i < r[i]) std::swap(A[i], A[r[i]]);
	for(int l = 1; l < len; l <<= 1) {
		int w0 = ksm(3, (mod - 1) / (l << 1));
		for(int i = 0; i < len; i += (l << 1)) {
			int w = 1, a0 = i, a1 = i + l;
			for(int k = 0; k < l; k++, a0++, a1++, w = 1LL * w * w0 % mod) {
				int tmp = 1LL * A[a1] * w % mod;
				A[a1] = ((A[a0] - tmp) % mod + mod) % mod;
				A[a0] = (A[a0] + tmp) % mod;
			}
		}
	}
	if(!(~flag)) {
		int inv = ksm(len, mod - 2);
		std::reverse(A.begin() + 1, A.end());
		for(int i = 0; i < len; i++) A[i] = 1LL * A[i] * inv % mod;
	}
}
vector<int> operator * (vector<int> A, vector<int> B) {
	int tot = A.size() + B.size() - 1;
	for(len = 1; len <= tot; len <<= 1);
	for(int i = 0; i < len; i++) r[i] = (r[i >> 1] >> 1) | ((i & 1) * (len >> 1));
	FNTT(A, 1), FNTT(B, 1);
	vector<int> C;
	for(int i = 0; i < len; i++) C.push_back(1LL * A[i] * B[i] % mod);
	FNTT(C, -1);
	C.resize(tot);
	return C;
}
int n, m, fac[maxn], inv[maxn], S, w[maxn];
int C(int x, int y) { return 1LL * fac[x] * inv[y] % mod * inv[x - y] % mod; }
void predoit() {
	fac[0] = 1;
	for(int i = 1; i < maxn; i++) fac[i] = 1LL * fac[i - 1] * i % mod;
	inv[maxn - 1] = ksm(fac[maxn - 1], mod - 2);
	for(int i = maxn - 2; i >= 0; i--) inv[i] = 1LL * inv[i + 1] * (i + 1) % mod;
}
int main() {
	n = in(), m = in(), S = in();
	predoit();
	for(int i = 0; i <= m; i++) w[i] = in();
	int limit = std::min(m, n / S);
	vector<int> A, B;
	for(int i = 0; i <= limit; i++) {
		A.push_back(1LL * C(m, i) * ksm(m - i, n - i * S) % mod * fac[n] % mod * ksm(inv[S], i) % mod * inv[n - i * S] % mod * fac[i] % mod);
		B.push_back((limit - i) & 1? mod - inv[limit - i] : inv[limit - i]);
	}
	A = A * B;
	int now = 0;
	for(int i = 0; i <= limit; i++) (now += 1LL * w[i] * A[i + limit] % mod * inv[i] % mod) %= mod;
	printf("%d\n", now);
	return 0;
}