动态规划问题（六）最长公共子序列（LCS）

问题描述

​ 给你两个字符串，要求得到这两个字符串的最长公共子序列长度。

​ 比如：对于输入的字符串 S1 "AGGTAB" 和 S2 "GXTXAYB"，它们的最长公共子序列长度为 4，为 {'G', 'T', 'A', 'B'}

解决思路

​ 该问题刚开始见到时没有思路，但是把问题细分一下找到规律即可解决。

• 递归

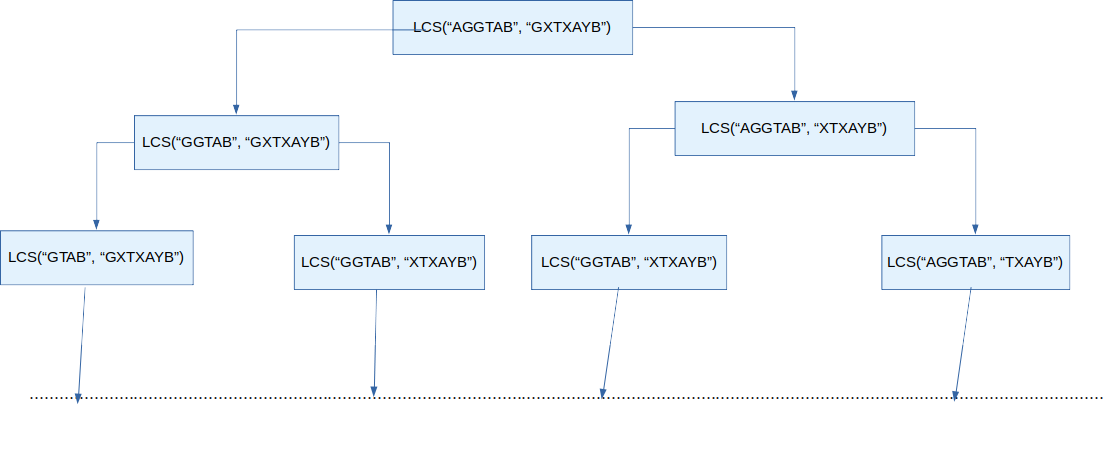
  • 对于当前输入的两个字符串，可以通过不断将两个字符串的分别移除来减小问题的规模，最终收敛

  • 以上文的输入为例，对于输入的 S1 “AGGTAB” 和 S2 “GXTXAYB”，首先将 S1 的第一个字符与 S2 的第一个字符比较，然后移除 S1 的第一个字符再与 S2进行比较…… 对 S2 做同样的操作。此时的情况如下图所示：

    

• 动态规划

  • 动态规划在这里的解决的是重复子问题的类型，由于上文的递归方案，在这个解决过冲中存在大量的重复计算，因此可以使用动态规划存储中间计算结果，从而提高运行效率。

实现

• 递归

  public class Solution {
      public static int lcs(String s1, String s2) {
          int len1 = s1.length(), len2 = s2.length();
  
          // 递归终止条件
          if (len1 == 1 || len2 == 1)
              return s1.charAt(0) == s2.charAt(0) ? 1 : 0;
  
          // 递归剩下的结果得到该问题的解
          if (s1.charAt(0) == s2.charAt(0))
              return Math.max(
                  lcsRecur(s1.substring(1), s2),
                  lcsRecur(s1, s2.substring(1))
              ) + 1;
  
          return Math.max(
              lcsRecur(s1.substring(1), s2),
              lcsRecur(s1, s2.substring(1))
          );
      }
  }
  

• 动态规划

  public class Solution {
      public static int lcs(String s1, String s2) {
          // 将字符串转变为对应的字符数组，提高查找的速度
      	char[] s1Arr = s1.toCharArray();
          char[] s2Arr = s2.toCharArray();
          int row = s1Arr.length, col = s2Arr.length;
  
          // 存储中间计算结果的二维数组
          int[][] dp = new int[row + 1][col + 1];
  
          for (int i = 1; i <= row; ++i) {
              for (int j = 1; j <= col; ++j) {
                  if (s1Arr[i - 1] == s2Arr[j - 1])
                      dp[i][j] = dp[i - 1][j - 1] + 1; // 由于要保证当前的字符是在之前比较的字符之后的，因此需要得到的是左上角的元素中间值
                  else
                      dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
              }
          }
  
          return dp[row][col];
      }
  }