再探 游戏 《 2048 》 —— AI方法—— 缘起、缘灭（8） —— 2021年9月SOTA的TDL算法——《Optimistic Temporal Difference Learning for 2048》——完结篇

《2048》游戏在线试玩地址：

https://play2048.co/

如何解决《2048》游戏源于外网的一个讨论帖子，而这个帖子则是讨论如何解决该游戏的最早开始，可谓是“缘起”:

What is the optimal algorithm for the game 2048?

关于该游戏的相关内容前面已经写过一些内容：

再探 游戏 《 2048 》 —— AI方法—— 缘起、缘灭（1） —— Firefox浏览器下自动运行游戏篇

=====================================================

之前曾经写过一篇《2048》游戏TD解法的SOTA论文的博客：

再探 游戏 《 2048 》 —— AI方法—— 缘起、缘灭（4） —— state-of-the-art

不过，后来发现上面这个博客的论文：

Mastering 2048 with Delayed Temporal Coherence Learning, Multi-Stage Weight Promotion, Redundant Encoding and Carousel Shaping

在2021年9月被论文《Optimistic Temporal Difference Learning for 2048》所超越，其实超越的幅度并不大，在游戏达到2**15=32768方块数值的回合数episodes上高出了2%，而这个成绩的获得也伴随着更多的训练episodes，总的来看训练的时间应该增加了几倍到几十倍的区间。

其实不管是上个SOTA的论文《Mastering 2048 with Delayed Temporal Coherence Learning, Multi-Stage Weight Promotion, Redundant Encoding and Carousel Shaping》

，还是现在的SOTA论文《Optimistic Temporal Difference Learning for 2048》，与最早的《2048》游戏的TD解法论文《Temporal difference learning of N tuple networks for the game 2048》其实改动并不大，就与现在SOTA的论文《Optimistic Temporal Difference Learning for 2048》为例，其实最大的改动就是对N-Tuple网络初始化时不设置为0而是设置为一个较大的数值，但是即使如此这两个论文的代码都难以复现和重新运行，当然最原始的论文代码还是可以很好运行的，其python版本个人还做了复现，见：再探 游戏 《 2048 》 —— AI方法—— 缘起、缘灭（7） —— Python版本实现的《2048》游戏的TDL算法。

论文代码的难以运行说明：

之所以现在SOTA的实现都难以运行，主要原因就是运算周期太长，这里以现在的SOTA论文《Optimistic Temporal Difference Learning for 2048》为例，其官方实现见：https://github.com/moporgic/TDL2048

可以看到，该代码的实现基本是C++然后加上各种并行和宏指令，代码难度较大，而且按照论文中的200M或300M个episodes的运行，其耗时是极为巨大的。根据官方的代码，使用i7-10700k cpu在5.0Ghz频率下单核运行1000k个episodes耗时25分钟，那么运行200M个episodes需要耗时(25*200)/60/24=3.472天，当然论文中指出在E5-2698 v4的CPU上运行66 小时就可以，但是这里需要知道，这是需要在企业级CPU上多核心并行运行而且不考虑内存不够用的前提下，然后需要66小时，而如果你是拿一个家用级别的CPU然后单核心运行，那么你就需要至少一个月到两个月的时间才可以运行完，而且注意，这里只是运行单次的时间。而且该论文的官方代码基本优化到了就差上汇编指令了，基本上可以认为是优化到了最快速度了，至于以后能不能用量子计算机来提速就不知道是否可行了。不得不说搞AI这么久，这么耗时的程序除了“阿拉法狗”以外这是我遇到的最耗时的了。

但是不得不说，官方给出的代码确实是优化得很好了，不过这么长的运行时间基本可以劝退其他人了。

学术价值上的思考：

《2048》游戏的解法最早是一群IT开发的程序员所提出并进行了大量讨论，最后还给出了启发式的解法。而后期的Reinforcement learning解法都是基于TD+n-tuple net的，可以说学术价值不大，并没有什么太多的学术问题存在，即使是现在SOTA的论文也是改动很小，基本就是把已经成形的算法移过来用上，但是即使是算法逻辑简单，但是工程实现方面却要求很大。以我实现的最原始的TD解法：再探 游戏 《 2048 》 —— AI方法—— 缘起、缘灭（7） —— Python版本实现的《2048》游戏的TDL算法来看，我运行100k个episodes的用时为5个小时，当然这是python版本实现的，运行效率自然不会太高，但是如果用这个版本就像200M个episodes的运行，那么需要时长为：(5*2000)/24=416.66天，即10000小时，这个运行时长基本可以用年来计算了，而作者给出的官方C++版本深度指令优化版本在企业级服务器并行运行需要66小时，其差距为151.5倍，当然C++版本的比python版本的快100倍也能理解，但是这个时长是真的难以接受，即使你用官方的优化后代码然后并行运行在企业家服务器上也是至少需要66小时。当然这个算法这么耗时主要原因就是在进行《2048》游戏时交互后游戏执行所耗费的时间，即使使用Intel cpu专属的位移指令最后的耗时也是难以接受的，200M个episodes再怎么优化这耗时也难以降的下来，不过这也是少见的一种需要如此多训练episodes的TD算法应用了。由于《2048》游戏的TD解法学术性不高并且高效C++版本实现如此困难再加上如此长的运行耗时，这个《2048》游戏的最优解法可能也就进展到这了，再继续探究这个好像意义价值也确实不大了。

关于TD+n-tuple net 的注意点：

在《2048》游戏的TD解法中，都是使用afterstate状态，也就是一次移动后游戏环境没有自动添加tile的那个状态，用这个状态来进行估计estimation。

由于使用的是n-tuple net，也就是查表法，不同于函数的近似表示，对于一条episode中的任意一个afterstate状态的更新对于其他afterstate状态的估计和更新影响不大，因此在所有的解法中都是获得整条episode的数据后再从最后的afterstate状态开始向前更新对应的n-tuple net中的数值的。从最后的afterstate状态开始向前更新，要比从第一个afterstate状态开始向后更新效率更高，因为最后一个afterstate的估计值为0，这样计算误差更低并且可以快速的向前修正整个episode中的afterstate的估计，整个update过程会更加高效。而之所以函数近似的TD算法都是使用一次估计然后执行，然后更新，这样是因为使用函数近似来表示状态数值的话对任意一个afterstae的更新都会对所有afterstate的估计产生影响，因此这样的更新方式更高效，而这里我们使用的是n-tuple net查表法，每个afterstate之间的关联度都不大，由于n-tuple net的规模很大，即使在一条episode中有些afterstate有共用的value，其影响度也极为有限。因此，在TD+N-Tuple net的配置中，很重要的一点就是搜集完整条episode数据后从后向前更新afterstate状态的估计值，这一点关键。

借鉴意义：

即使前面说了《2048》游戏最优解法的学术意义不大，继续研究和探讨的意义不大，不过这个问题所引起的一系列的讨论和解法确实还是蛮有趣的，而且对我们也有蛮的启发和借鉴意义的。

论文《Optimistic Temporal Difference Learning for 2048》的主要内容介绍：

主要工作：

1. 对n-tuple net的权重不再初始化为0或随机，而是初始化为一个较大的数值。由于我们都是使用episode数据从后向前更新afterstate估计，因此这样的初始化可以使算法对于没有执行过的状态给与更大的被选择机会。

2. 引入TD算法的优化学习率的TC算法，构成混合算法，也就是TD算法执行10%个episode后执行TC算法，TC算法的初始学习率为1。

3. 使用多阶段的方式，即分层强化学习，比如100M个episodes为一个阶段，使用两个阶段，即200M个episodes。第一个阶段，大数值初始化N-tuple net，TD算法执行10%个episode（100M*10%）后执行TC算法；第二个阶段，从棋盘最大tile数值为2**14=16384的游戏状态开始，大数值初始化N-tuple net，TD算法执行10%个episode（100M*10%）后执行TC算法。

4. 在训练完成后测试时加入Expectimax Search，也就是加入树搜索，在每次树搜索时使用Tile-Downgrading方法，也就是对于某些最大tile较大的棋盘状态进行树搜索时，由于决策效果有限，于是将这个棋盘状态进行Tile-Downgrading。Tile-Downgrading就是找到棋盘状态中最大tile的数值到最小tile数值中第一个断掉的不连贯的tile数值，然后将大于该数值的所有tile的数值都除2，于是形成新的棋盘状态，在这一次的树搜索过程中root状态就使用这个新的棋盘状态进行。如下图：

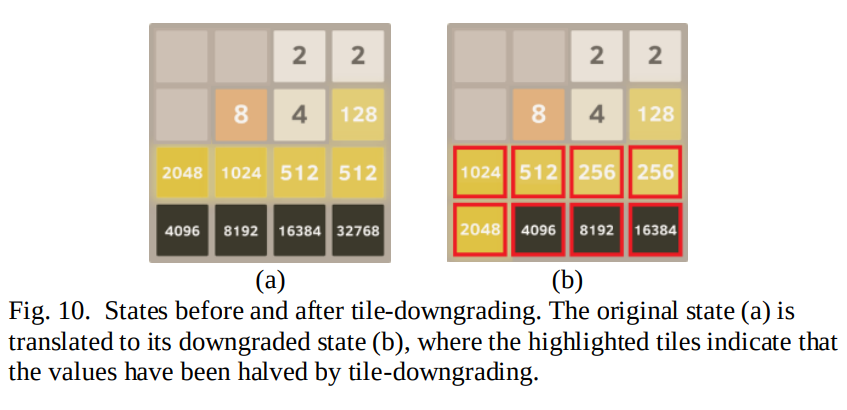
由于256是第一个断开的tile数值，于是将所有大于这个数值的tile均除2，形成新的棋盘状态后用其进行树搜索，最后得到的决策动作用于原始的棋盘状态（进行树搜索之前的原始状态的决策）。

============================

个人感觉，这篇论文中最有原创的工作，第一个是初始化权重使用较大数值，第二个就是这个树搜索时使用Tile-Downgrading。

不过即使这篇论文做了这些工作，不过最后对最终结果影响最大的还是多阶段的设计，也就是multi-stage，也可以看做是分层强化学习，即使本篇论文只使用了2个阶段，并不像上个论文使用了16个阶段，不过也正是由于使用了这个多阶段才最终获得了最好的成绩。

----------------------------------------------

一些个人认为可能有用的改进：

使用缓存池设计：

感觉主要是研究《2048》游戏解法的人比较少，现在Reinforcment learning的很多SOTA的方法其实都是可以用在这里的，比如使用缓冲池的方法，这样就可以提高数据的利用率了，当然具体如何使用还是需要具体去调的，不过由于这个《2048》游戏现在发展的形式已经很难会有人真的去调这个了。在这里如果使用缓冲池，如何存储数据，不同的最大tile的棋盘数据是否按照一定的比例去存储都是需要考虑的问题，比如在这个游戏解法中往往tile越大的棋盘状态越少，那么我们是不是可以在训练一定episodes后尽量多存储max tile较大的那些状态数据呢。不过使用multi-stage的分层强化学习后，和这里的这个按比例存储就很像了，比如在第二个stage里面就很像缓冲池只存储2**14=16384以上的棋盘状态，不过即使这样multi-stage+缓冲池设计也会有望提高训练的效率。

使用epsilon-greedy设计增加探索性：

之所以在max tile较小的时候训练的好，较大的时候训练的差，个人观点就是max tile较小的时候棋盘中空格数量多，环境随机性大，而且每种动作选择可能都会有一个较好的搜获（可以理解为每个动作的Q值都很高，并且相差不大），这个时候不使用epsilon-greedy探索机制往往也可以获得比较好的结果；但是在max tile较大的时候，空格较少，环境的随机性较差，不同动作的Q值往往可能相差很大，这时候就需要较大探索力度，而这时候可以考虑使用epsilon-greedy探索机制。比如在《Optimistic Temporal Difference Learning for 2048》论文算法中的第二阶段加入epsilon-greedy探索机制。

一些个人的理解：

其实可以看到，尤其《2048》棋盘数据的分布不规整性（数值分布为0，1，2，3，......，16）比较适合使用n-tuple网络；棋盘的max tile的数值在较小和较大时整个游戏环境差别是很大的，主要就是空格数量的多少，因此在max tile较小时训练的n-tuple net可能不适合于max tile较大时的棋盘状态，因此使用multi-stage方式的分层强化学习会有很大提升。即使max tile较大时棋盘状态也会有空格较多的情况，但是往往只需要几步移动就会轻易的出现空格较少的情况，因为max tile很大，所以即使很好的移动也往往不会很好的消减掉棋盘上的tile。《Optimistic Temporal Difference Learning for 2048》中提出的大数值初始化n-tuple net权重的设计其实更适合max tile较大的情况，比如multi-stage中的第二阶段。

===============================================

 附：

Expectimax Search和Tile-Downgrading都是在测试时候加入的，并不是在训练时候使用的。