FFT & NTT 及其简单优化

FFT

FFT 是一种高效实现 DFT 和 IDFT 的方式，可以在 $O(n \log n)$ 的时间内求多项式的乘法。

多项式的点值表示

不同于用每项的系数来表示一个多项式，我们知道对于给定的 $n+1$ 个点值，可以确定唯一的 $n$ 次多项式。这种用点值表示多项式的方法叫点值表示法。

如果知道 $F(x)$ 和 $G(x)$ 的点值表示，求出 $F(x)\times G(x)$ 的点值表示是 $O(n+m)$ 的。复杂度瓶颈变成了如何快速转换多项式的两种表示形式。

把系数转成点值的算法叫 离散傅里叶变换(DFT)，相应地，把点值转成系数的算法叫 逆离散傅里叶变换(IDFT)。

DFT

前置知识：单位根

OIWiki-复数-单位根

已经说过，要选取 $n$ 个点并求出它们对应 $F(x)$ 的值。先观察 $F(x)$ 的性质：

\[F(x)=a_0+a_1x+a_2x^2+a_3x^3+a_4x^4+a_5x^5+a_6x^6+a_7x^7
\]

把奇偶项分开，得

\[F(x)=(a_0+a_2x^2+a_4x^4+a_6x^6)+(a_1x+a_3x^3+a_5x^5+a_7x^7)\\
F(x)=(a_0+a_2x^2+a_4x^4+a_6x^6)+x(a_1+a_3x^2+a_5x^4+a_7x^6)\\
F(x)=G(x^2)+x\times H(x^2)
\]

似乎看起来对每个 $x$ 求 $G$ 和 $H$，要求的还是 $n$ 个值。但这时单位根的性质就能用上了：

令 $x$ 分别为 $\omega_n^1,\omega_n^2,...,\omega_n^n$，那么有：

\[\begin{aligned}
F(\omega_n^k)&=G(\omega_n^{2k})+x\times H(\omega_n^{2k})\\
&=G(\omega_{n/2}^k)+x\times H(\omega_{n/2}^k)

\end{aligned}
\]

根据 $\omega_n^{k}=-\omega_n^{k+n/2}$，且 $G,H$ 均为偶函数，可以得到：

\[F(\omega_n^{n/2+k})=G(\omega_{n/2}^{k})-x\times H(\omega_{n/2}^{k})
\]

发现这是好的，因为只用求前一半的 $G$ 和 $H$ 的值就可以了，把它们两个分别递归处理即可。

但是 FFT 只能对次数为 $2^m$ 的多项式这么做，所以如果多项式不是恰好 $2^m$ 项，需要在后面用一些系数为 $0$ 的项把它补满。

IDFT

想完成多项式乘法，还要把点值表示重新转换回系数表示，这个过程叫 IDFT。

构造方法实在过于神秘，以至于菜猫猫并不能理解这个思路的由来，所以这里直接给出做法：

设对 $F(x)$ 进行 DFT 后得到点值表示 $y_0,y_1,...y_{n-1}$，构造 $G(x)=y_0+y_1x+...+y_{n-1}x^{n-1}$。

将 $x=\omega_n^0,\omega_n^{-1}...\omega_n^{-(n-1)}$ 代入，得：

\[\begin{aligned}
G(\omega_n^{-k})&=\sum\limits_{i=0}^{n-1} y_i \omega_n^{-ki}\\
&=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1} a_j\times (\omega_n^i)^j\times \omega_n^{-ki}\\
&=\sum_{j=0}^{n-1}a_j \sum_{i=0}^{n-1}(\omega_n^{j-k})^i
\end{aligned}
\]

那么当且仅当 $j=k$，$G=a_k\times n$。因此对 $G(x)$ 代入 $x=\omega_n^0,\omega_n^{-1}...\omega_n^{-(n-1)}$ 求 DFT，结果除以 $n$ 即为多项式的各项系数。

实现上可以设定一个参数为 $1$ 或 $-1$ 传入 DFT 函数，减小码量。

蝶形运算

一个很诈骗的东西。不要被网上这种图吓到了：

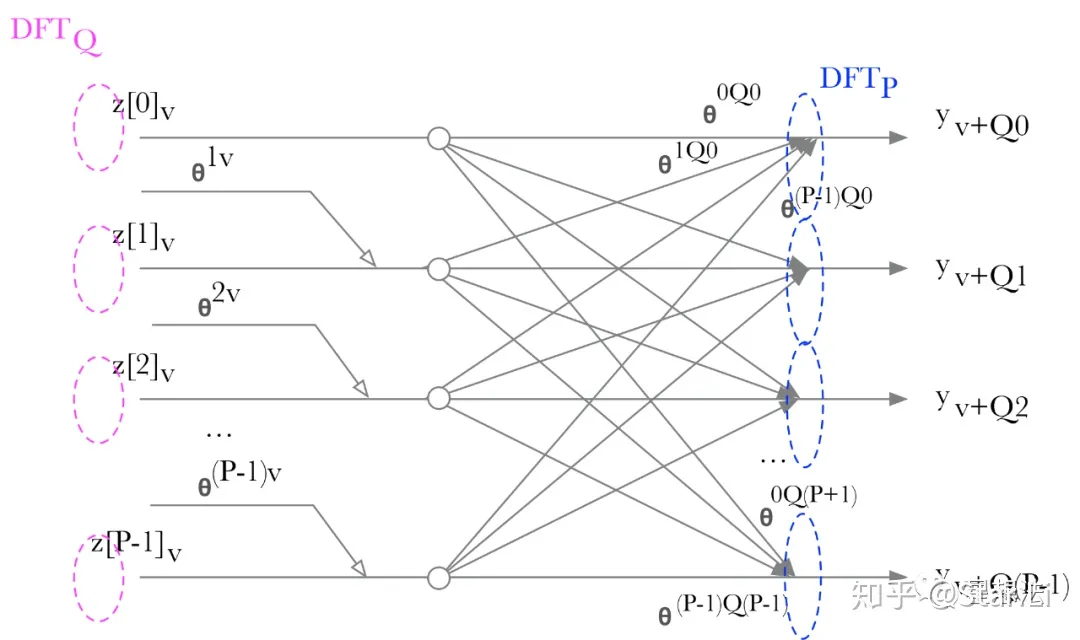
通俗地讲，其实就是，我们通过 $G(\omega_{n/2}^k)$ 和 $H(\omega_{n/2}^k)$ 求 $F(\omega_{n}^k)$、$F(\omega_{n}^{k+n/2})$ 时，本来需要额外开一个数组；

但你发现 $G,H$ 存储的位置和你要把 $F$ 求完存储的位置是同一个，且求其他位置 $F$ 的值时也不再用到这两个数据，一边求一边覆盖是不影响正确性的。

讲完了，跟蝶形确实没什么关系对吧。

实现-递归版

众所周知 c++ 自带的 complex 类常数极大，建议手写。

至此，我们可以写出朴素的递归版本 FFT 了：

递归 FFT

void FFT(int limit,Complex a[],int op)

{

	if(limit==1) return;

	Complex a1[(limit>>1)+5],a2[(limit>>1)+5];

	for(int i=0;i<=limit;i+=2) a1[i>>1]=a[i],a2[i>>1]=a[i+1];

	FFT(limit>>1,a1,op),FFT(limit>>1,a2,op);

	Complex Wn={cos(2.0*pai/limit),sin(2.0*pai/limit)*op},w={1,0};

	for(int i=0;i<(limit>>1);i++,w=w*Wn)

	{

		a[i]=a1[i]+w*a2[i];

		a[i+(limit>>1)]=a1[i]-w*a2[i];

	}

}

int main()

{

	n=read(),m=read();

	for(int i=0;i<=n;i++) a[i].x=read();

	for(int i=0;i<=m;i++) b[i].x=read();

	int w=1;while(w<=m+n) w<<=1;

	FFT(w,a,1),FFT(w,b,1);

	for(int i=0;i<=w;i++) a[i]=a[i]*b[i];

	FFT(w,a,-1);

	for(int i=0;i<=n+m;i++) printf("%d ",(int)(a[i].x/w+0.5));

	return 0;

}

位逆序置换

递归的常数太大了，接下来讲讲怎么不递归。

考虑每次把系数按奇偶分开的过程，即把下标以二进制的最后一位为关键字排序。也就是说，把二进制倒过来看，如果 $i$ 按位翻转后为 $j$，那么下标为 $i$ 的数操作到最后就会跑到位置 $j$ 上。

这启发我们使用迭代实现，预处理出每个系数最后所在的位置，直接从底层倒推即可。

const int N=4e6+5;

const double pi=acos(-1);

int n,m,limit=1;

struct Complex {double x,y;}a[N],b[N];

il Complex operator +(Complex a,Complex b) {return {a.x+b.x,a.y+b.y};}

il Complex operator -(Complex a,Complex b) {return {a.x-b.x,a.y-b.y};}

il Complex operator *(Complex a,Complex b) {return {a.x*b.x-a.y*b.y,a.x*b.y+a.y*b.x};}

int to[N];

void FFT(Complex *a,int tp)

{

	for(int i=0;i<limit;i++) if(i<to[i]) swap(a[i],a[to[i]]);

	for(int len=1;len<limit;len<<=1)

	{

		Complex Wn={cos(pi/len),sin(pi/len)*tp};

		for(int i=0;i<limit;i+=(len<<1))

		{

			Complex w={1,0};

			for(int j=0;j<len;j++,w=w*Wn)

			{

				Complex x=a[i+j],y=w*a[i+len+j];

				a[i+j]=x+y,a[i+len+j]=x-y;

			}

		}

	}

}

int main()

{

	n=read(),m=read();

	for(int i=0;i<=n;i++) a[i].x=read();

	for(int i=0;i<=m;i++) b[i].x=read();

	int k=0; while(limit<=n+m) limit<<=1,k++;

	for(int i=0;i<limit;i++) to[i]=(to[i>>1]>>1)|((i&1)<<(k-1));

	FFT(a,1),FFT(b,1);

	for(int i=0;i<limit;i++) a[i]=a[i]*b[i];

	FFT(a,-1);

	for(int i=0;i<=n+m;i++) printf("%d ",(int)(a[i].x/limit+0.5));

	return 0;

}

三次变两次优化

上文中，进行两个多项式相乘时，我们需要调用三次 FFT 函数：对 $F$ 和 $G$ 分别 DFT，对 $F\times G$ IDFT。这么做是不够优的。

这里就可以用到三次变两次优化的技巧，使常数减小三分之一。

具体地，我们在计算前直接把 $G$ 放在 $F$ 的虚部上，乘法操作变为计算 $F(x)$ 平方。

答案就是 $F^2(x)$ 的虚部除以 $2$。

正确性证明是容易的：$(a+b\text{i})^2=(a^2-b^2)+2ab\text{i}$。

在主函数上稍作改动即可：

int main()

{

	n=read(),m=read();

	for(int i=0;i<=n;i++) a[i].x=read();

	for(int i=0;i<=m;i++) a[i].y=read();//here

	int k=0; while(limit<=n+m) limit<<=1,k++;

	for(int i=0;i<limit;i++) to[i]=(to[i>>1]>>1)|((i&1)<<(k-1));

	FFT(a,1);

	for(int i=0;i<limit;i++) a[i]=a[i]*a[i];//and here

	FFT(a,-1);

	for(int i=0;i<=n+m;i++) printf("%d ",(int)(a[i].y/2/limit+0.5));

	return 0;

}

NTT

前置知识-原根

阶：使得 $a^n\equiv1\pmod{m}$ 的最小正整数 $n$ 称为 $a$ 模 $m$ 的阶。

原根：若 $\gcd(g,m)=1$，且 $\delta_m(g)=\varphi(m)$，则 $g$ 是 $m$ 的原根。

存在定理 一个数 $m$ 存在原根当且仅当 $m=2,4,p^{\alpha},2p^{\alpha}$，其中 $p$ 为奇素数，$\alpha \in \mathbb{N}^{*}$。

判定定理 设 $m\ge 3,\gcd(a,m)=1$，则 $a$ 是模 $m$ 的原根的充要条件是，对于 $\varphi (m)$ 的每个质因数 $p$，都有 $a^{\frac{\varphi(m)}{p}}\not\equiv 1\pmod m$。

原根个数 若一个数有原根，则它原根的个数为 $\varphi(\varphi(m))$。

以上结论的证明：link

NTT 用来解决模意义下的多项式乘法问题，其运算均为整数，在常数和精度方面均优于 FFT。（划掉，实测还是 FFT 跑得快。

原根的性质与单位根类似，因此我们把 FFT 中所有 $\omega_n$ 替换成 $g^{\frac{p-1}{n}}$，乘 $-1$ 换成乘逆元即可。

NTT 的常见模数是 $998244353$，它的原根是 $3$。

为什么我的 NTT 跑得比 FFT 慢啊 /dk

#define int long long

const int N=4e6+5,mod=998244353;

il int qpow(int n,int k=mod-2)

{

	int res=1;

	for(;k;n=n*n%mod,k>>=1) if(k&1) res=res*n%mod;

	return res;

}

int n,m,a[N],b[N],inv=qpow(3),limit=1,to[N];

il void NTT(int *a,int tp)

{

	for(int i=0;i<limit;i++) if(i<to[i]) swap(a[i],a[to[i]]);

	for(int len=1;len<limit;len<<=1)

	{

		int Wn=qpow(tp>0?3:inv,(mod-1)/(len<<1));

		for(int i=0;i<limit;i+=(len<<1))

			for(int j=0,w=1;j<len;j++,w=w*Wn%mod)

			{

				int x=a[i+j],y=w*a[i+len+j]%mod;

				a[i+j]=(x+y)%mod,a[i+len+j]=(x-y+mod)%mod;

			}

	}

}

signed main()

{

	n=read(),m=read();

	for(int i=0;i<=n;i++) a[i]=read();

	for(int i=0;i<=m;i++) b[i]=read();

	int k=0; while(limit<=m+n) limit<<=1,k++;

	for(int i=0;i<limit;i++) to[i]=(to[i>>1]>>1)|((i&1)<<(k-1));

	NTT(a,1),NTT(b,1);

	for(int i=0;i<limit;i++) a[i]=a[i]*b[i]%mod;

	NTT(a,-1);

	for(int i=0;i<=n+m;i++) printf("%lld ",a[i]*qpow(limit)%mod);

	return 0;

}