"山海经“ 讲解----线段树

”山海经“--线段树 讲解

1、题面：

http://cogs.pro/cogs/problem/problem.php?pid=775

2、题目大意及分析：

i：大概就是说给了你一段[1,n]的区间，并给了每个区间的权值，下面会有m个问题，每个问题给你一段[1,n]的子区间[i,j]，问你在这段区间上的任意一端子区间和最大是多少，并且要求输出这段区间，然后最恶心的点就是这段区间要保证是在sum最大的情况下，优先i最小，其次j最小(这真的是缺德至极了)。

ii：那既然是线段树的题我们一开始很容易就会想到用线段树来维护一段区间的sum以及maxn，只不过是把一个求和和一个最大值搓在一起了吗，（然后我吭哧吭哧打出来，发现连样例都过不了），为什么错了呢，再给大家看一下样例：

样例输入

5 3

5 -6 3 -1 4

1 3

1 5

5 5

样例输出

1 1 5

3 5 6

5 5 4

那么按照我们的思路，线段树画出来是这样的：



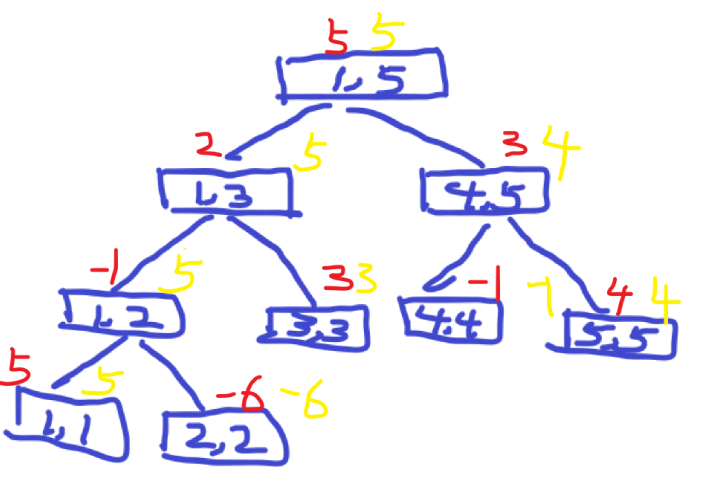
(红色标记为sum，黄色标记为maxn)

明显发现[1,5]是错的，可由[3,5]转移过来6.

我们这样的做法表明了每段区间的的sum值和maxn值都只是由我们给划分好的区间转移过来，就像是区间[1,5]只能由[1,3]和[4,5]转移过来，却没有想到我们划分好的区间其实是可以打通的，就像区间[1,5],被分成了[1,3]和[4,5]，但实际答案是[3,5]。这就警示了我们去深入思考，像[1,5]中的[3,5]这样是从中间打通的，但一定要注意是以中间为基准的，必须由中间向两边扩展，(不能找出左右两边的maxn再加和，因为题目中明确说了i只能到达i+1，所以道路必须是连续不断的)，那么怎么算呢，遍历一遍？

NO，TLE终止了我的美梦。

第一次交的代码：

面对TLE的$\huge{pu-tao↑zher↑↓}$

#include<bits/stdc++.h>
#define ps push_back
#define mk make_pair
using namespace std;
typedef long long ll;
const int MAXN=0x7fffffff;
const int N=1e5+10;
int a[N],n,m,pre[N];
struct jj{
	int sum=0,max=-MAXN;
	int l,r;
	pair<int,int> ans;
}tr[N<<2];
//int sum(int L,int R,int l,int r,int k){
//	if(L<=l&&r<=R)return tr[k].sum;
//	else{
//		int ans=0;
//		int mid=l+r>>1;
//		if(L<=mid)ans+=sum(L,R,l,mid,k<<1);
//		if(R>mid)ans+=sum(L,R,mid+1,r,k<<1|1);
//		return ans;
//	}
//}
inline void geng(int x){
	tr[x].sum=tr[x<<1].sum+tr[x<<1|1].sum;
	int j1=-MAXN,j2=-MAXN,mid=tr[x].l+tr[x].r>>1,l,r,p;
	if(tr[x].max<tr[x].sum)tr[x].max=tr[x].sum,tr[x].ans=mk(tr[x].l,tr[x].r);
	if(tr[x].max<tr[x<<1].max)tr[x].max=tr[x<<1].max,tr[x].ans=tr[x<<1].ans;
	if(tr[x].max<tr[x<<1|1].max)tr[x].max=tr[x<<1|1].max,tr[x].ans=tr[x<<1|1].ans;
	for(int i=tr[x].l;i<=mid;i++){
		p=pre[mid]-pre[i-1];
		if(j1<p)j1=p,l=i;
	}
	for(int i=mid+1;i<=tr[x].r;i++){
		p=pre[i]-pre[mid];
		if(j2<p)j2=p,r=i;
	}
	if(tr[x].max<j1+j2)tr[x].max=j1+j2,tr[x].ans=mk(l,r);
}
void jian(int k,int l,int r){
	tr[k].l=l,tr[k].r=r;
	if(l==r){
		tr[k].sum=a[l];
		tr[k].max=a[l];
		tr[k].ans=mk(l,r);
		return;
	}
	int mid=(l+r)>>1;
	jian(k<<1,l,mid);
	jian(k<<1|1,mid+1,r);
	geng(k);
}
struct ret{
	int ans;
	pair<int,int> key;
	void out(){
		printf("%d %d %d\n",key.first,key.second,ans);
	}
};
ret ask(int L,int R,int l,int r,int k){
	if(L<=l&&r<=R)return ret{tr[k].max,tr[k].ans};
	else{
		int mid=l+r>>1;
		ret anss=ret{-MAXN};
		if(L<=mid){
			ret pp=ask(L,R,l,mid,k<<1);
			if(anss.ans<pp.ans)anss=pp;
		}
		if(L<=mid&&R>mid){
			int l1,r1,p,j1=-MAXN,j2=-MAXN;
			for(int i=L;i<=mid;i++){
				p=pre[mid]-pre[i-1];
				if(j1<p)j1=p,l1=i;
			}
			for(int i=mid+1;i<=R;i++){
				p=pre[i]-pre[mid];
				if(j2<p)j2=p,r1=i;
			}
			if(anss.ans<j1+j2)anss.ans=j1+j2,anss.key=mk(l1,r1);
		}
		if(R>mid){
			ret pp=ask(L,R,mid+1,r,k<<1|1);
			if(anss.ans<pp.ans)anss=pp;
		}
		return anss;
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++)scanf("%d",&a[i]),pre[i]=pre[i-1]+a[i];
	jian(1,1,n);
//	for(int i=1;i<=n*4;i++)cout<<tr[i].sum<<' '<<tr[i].max<<' '<<i<<' '<<tr[i].l<<' '<<tr[i].r<<' '<<tr[i].ans.first<<' '<<tr[i].ans.second<<endl;
	int x,y;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		ret op=ask(x,y,1,n,1);
		op.out();
	}
}

那怎么办，要不存一下每段区间从mid向两边拓展的最大值？刚要动手打，发现每次还是得求一边，并且这个参数只能用于比较，没什么别的用，于是我就打开了题解，于是我就学到了这道题的精髓：每个区间的mid拓展最大值是由他的—————— 左二分区间的以右为基础向左拓展的最大值与—————— 右二分区间的以左为基础向右拓展的最大值的加和。

好，来总结一下：

1、优先级：

i.子区间和最大。

ii.子区间左端点i最小。

iii.子区间右端点j最小。

2、结构体中参数及其转移：

• i.左端点l，右端点r，建树时直接赋值。
• ii.sum求和，由两个二分区间的sum值加和转移过来。
• iii.以左为基础的向右拓展的最大值lman，以及这段区间的终点lmr(l-sum-r),可以由左二分区间的lman、左二分区间的sum+右二分区间的lman转移过来，且左二分区间的lman优先(因为左二分区间的lman的终点lmr一定小于右二分区间的lmr)。以右为基础的向左拓展的最大值rman，以及这段区间的终点rml(r-sum-l),可以由右二分区间的rman、右二分区间的sum+左二分区间的rman转移过来，且右二分区间的sum+左二分区间的rman优先，不知道为什么网上的题解大都按第一个右二分区间的rman优先，大概是没多想直接和上面一样了吧。
• iiii.该区间的子区间求和最大值man，man所对应的区间的两个端点ansl，ansr，man可以由左二分区间的man、右二分区间的man以及左二分区间的rman+右二分区间的lman转移过来，如果在值相等的情况下，左二分区间 优先于 中间加和 优先于 右二分区间。

注意：ii--iiii的转移不仅要出现在pushup函数中，而且也要在询问的ask函数中出现。

pushup函数：

void pushup(int k){//k是线段树的下标。
	int lid=k<<1,rid=k<<1|1;
	tr[k].sum=tr[lid].sum+tr[rid].sum;
	if(tr[k].lman<tr[lid].lman)tr[k].lman=tr[lid].lman,tr[k].lmr=tr[lid].lmr;
	if(tr[k].lman<tr[lid].sum+tr[rid].lman)tr[k].lman=tr[lid].sum+tr[rid].lman,tr[k].lmr=tr[rid].lmr;
	if(tr[k].rman<tr[rid].sum+tr[lid].rman)tr[k].rman=tr[rid].sum+tr[lid].rman,tr[k].rml=tr[lid].rml;
	if(tr[k].rman<tr[rid].rman)tr[k].rman=tr[rid].rman,tr[k].rml=tr[rid].rml;
	if(tr[k].man<tr[lid].man)tr[k].man=tr[lid].man,tr[k].ansl=tr[lid].ansl,tr[k].ansr=tr[lid].ansr;
	if(tr[k].man<tr[lid].rman+tr[rid].lman)tr[k].man=tr[lid].rman+tr[rid].lman,tr[k].ansl=tr[lid].rml,tr[k].ansr=tr[rid].lmr;
	if(tr[k].man<tr[rid].man) tr[k].man=tr[rid].man,tr[k].ansl=tr[rid].ansl,tr[k].ansr=tr[rid].ansr;
}

ask函数：

jj ask(int l,int r,int L,int R,int k){
	if(L<=l&&r<=R)return tr[k];
	else{
		int mid=l+r>>1,lid=k<<1,rid=k<<1|1;
		if(R<=mid)return ask(l,mid,L,R,lid);
		if(L>mid)return ask(mid+1,r,L,R,rid);
		jj ll,rr,z;
		ll=ask(l,mid,L,R,lid),rr=ask(mid+1,r,L,R,rid);
		if(z.lman<ll.lman)z.lman=ll.lman,z.lmr=ll.lmr;
		if(z.lman<ll.sum+rr.lman)z.lman=ll.sum+rr.lman,z.lmr=rr.lmr;
		if(z.rman<rr.sum+ll.rman)z.rman=rr.sum+ll.rman,z.rml=ll.rml;
		if(z.rman<rr.rman)z.rman=rr.rman,z.rml=rr.rml;
		if(z.man<ll.man)z.man=ll.man,z.ansl=ll.ansl,z.ansr=ll.ansr;
		if(z.man<ll.rman+rr.lman)z.man=ll.rman+rr.lman,z.ansl=ll.rml,z.ansr=rr.lmr;
		if(z.man<rr.man) z.man=rr.man,z.ansl=rr.ansl,z.ansr=rr.ansr;
		return z;
	}
}

3、初始化

注意sum=0,lman=rman=man=-0x7fffffff;

建树时遇到l==r的情况后要注意所有参数全部赋值：

build函数：

void build(int l,int r,int k){
	tr[k].l=l,tr[k].r=r;
	int mid=l+r>>1;
	if(l==r){
		tr[k].lmr=tr[k].rml=tr[k].ansl=tr[k].ansr=l;
		tr[k].lman=tr[k].rman=tr[k].man=tr[k].sum=a[l];
		return;
	}
	build(l,mid,k<<1);build(mid+1,r,k<<1|1);
	pushup(k);
}

附上最后代码

#include<bits/stdc++.h>
using namespace std;
const int N=1e5+10;
const int MAXN=0x7fffffff;
struct jj{
	int l,r,sum=0,lman=-MAXN,rman=-MAXN,ansl,ansr,lmr,rml,man=-MAXN;
}tr[N<<2];
int n,m,a[N];
void pushup(int k){
	int lid=k<<1,rid=k<<1|1;
	tr[k].sum=tr[lid].sum+tr[rid].sum;
	if(tr[k].lman<tr[lid].lman)tr[k].lman=tr[lid].lman,tr[k].lmr=tr[lid].lmr;
	if(tr[k].lman<tr[lid].sum+tr[rid].lman)tr[k].lman=tr[lid].sum+tr[rid].lman,tr[k].lmr=tr[rid].lmr;
	if(tr[k].rman<tr[rid].sum+tr[lid].rman)tr[k].rman=tr[rid].sum+tr[lid].rman,tr[k].rml=tr[lid].rml;
	if(tr[k].rman<tr[rid].rman)tr[k].rman=tr[rid].rman,tr[k].rml=tr[rid].rml;
	if(tr[k].man<tr[lid].man)tr[k].man=tr[lid].man,tr[k].ansl=tr[lid].ansl,tr[k].ansr=tr[lid].ansr;
	if(tr[k].man<tr[lid].rman+tr[rid].lman)tr[k].man=tr[lid].rman+tr[rid].lman,tr[k].ansl=tr[lid].rml,tr[k].ansr=tr[rid].lmr;
	if(tr[k].man<tr[rid].man) tr[k].man=tr[rid].man,tr[k].ansl=tr[rid].ansl,tr[k].ansr=tr[rid].ansr;
}
void build(int l,int r,int k){
	tr[k].l=l,tr[k].r=r;
	int mid=l+r>>1;
	if(l==r){
		tr[k].lmr=tr[k].rml=tr[k].ansl=tr[k].ansr=l;
		tr[k].lman=tr[k].rman=tr[k].man=tr[k].sum=a[l];
		return;
	}
	build(l,mid,k<<1);build(mid+1,r,k<<1|1);
	pushup(k);
}
jj ask(int l,int r,int L,int R,int k){
	if(L<=l&&r<=R)return tr[k];
	else{
		int mid=l+r>>1,lid=k<<1,rid=k<<1|1;
		if(R<=mid)return ask(l,mid,L,R,lid);
		if(L>mid)return ask(mid+1,r,L,R,rid);
		jj ll,rr,z;
		ll=ask(l,mid,L,R,lid),rr=ask(mid+1,r,L,R,rid);
		if(z.lman<ll.lman)z.lman=ll.lman,z.lmr=ll.lmr;
		if(z.lman<ll.sum+rr.lman)z.lman=ll.sum+rr.lman,z.lmr=rr.lmr;
		if(z.rman<rr.sum+ll.rman)z.rman=rr.sum+ll.rman,z.rml=ll.rml;
		if(z.rman<rr.rman)z.rman=rr.rman,z.rml=rr.rml;
		if(z.man<ll.man)z.man=ll.man,z.ansl=ll.ansl,z.ansr=ll.ansr;
		if(z.man<ll.rman+rr.lman)z.man=ll.rman+rr.lman,z.ansl=ll.rml,z.ansr=rr.lmr;
		if(z.man<rr.man) z.man=rr.man,z.ansl=rr.ansl,z.ansr=rr.ansr;
		return z;
	}
}
int main(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		scanf("%d",&a[i]);
	}
	build(1,n,1);
	int x,y;
	for(int i=1;i<=m;i++){
		scanf("%d%d",&x,&y);
		jj ans=ask(1,n,x,y,1);
		printf("%d %d %d\n",ans.ansl,ans.ansr,ans.man);
	}
}

[==============================================]

记得我说的网上的题解的bug吧？

给出hack代码：

hack.in:

8 1

1 2 0 0 398 -398 398 -37

3 8

hack.out:

3 5 398