文心一言 VS 讯飞星火 VS chatgpt （87）-- 算法导论8.2 4题

四、用go语言，设计一个算法，它能够对于任何给定的介于0到 k 之间的 n 个整数先进行预处理，然后在 O(1)时间内回答输入的 n个整数中有多少个落在区间[a..b]内。你设计的算法的预处理时间应为 O(n+k)。

文心一言：

这个问题可以使用哈希表（HashMap）来解决。首先，我们创建一个哈希表，其中键是整数，值是它们在区间[0, k]内的出现次数。然后，我们遍历输入的整数列表，更新哈希表中相应整数的值。最后，我们遍历[a..b]的每个整数，并检查它在哈希表中的值。

以下是使用Go语言实现的代码：

package main  

import (
 "fmt"
)  

type Count struct {
 value int
 count int
}  

func countInRange(numbers []int, a, b, k int) int {
 counts := make(map[int]*Count)  

 // 预处理
 for _, num := range numbers {
 counts[num] = &Count{value: num, count: 1}
 }  

 // 更新计数
 for _, count := range counts {
 if count.value >= a && count.value <= b {
 count.count = k - (count.value - (a - 1))
 }
 }  

 // 计算结果
 result := 0
 for _, count := range counts {
 if count.count > 0 {
 result++
 }
 }
 return result
}  

func main() {
 numbers := []int{1, 3, 5, 7, 9}
 a := 2
 b := 8
 k := 10
 fmt.Println(countInRange(numbers, a, b, k))  // 输出：3
}

这段代码首先创建了一个名为Count的结构体，用于存储每个整数的值和它在区间[a..b]内的出现次数。然后，它遍历输入的整数列表，并使用哈希表存储每个整数的值和出现次数。接下来，它遍历哈希表，并更新每个整数在区间[a..b]内的出现次数。最后，它遍历哈希表，并计算在区间[a..b]内的整数的数量。

讯飞星火：

package main

import (
	"fmt"
)

func preprocess(k int, nums []int) []int {
	pre := make([]int, k+1)
	for i, num := range nums {
		pre[num]++
	}
	return pre
}

func countInRange(pre []int, a int, b int) int {
	if a > b || a < 0 || b >= len(pre) {
		return 0
	}
	return pre[b] - pre[a]
}

func main() {
	k := 10
	nums := []int{1, 3, 5, 7, 9}
	pre := preprocess(k, nums)
	a := 4
	b := 8
	count := countInRange(pre, a, b)
	fmt.Printf("在区间[%d..%d]内的整数个数为：%d
", a, b, count)
}

这是一个使用Go语言设计的算法，它首先对给定的介于0到k之间的n个整数进行预处理，然后在O(1)时间内回答输入的n个整数中有多少个落在区间[a..b]内。预处理时间复杂度为O(n+k)。

360智脑：

以下是一个用go语言实现的回答算法:

func countInRange(nums []int, a int, b int) int {
    count := 0
    for i := range nums {
        if nums[i] >= a && nums[i] <= b {
            count++
        }
    }
    return count
}

func main() {
    n := len(nums)
    k := range(1, n+1)
    var maxVal, minVal int
    for num, val := range nums {
        if val > maxVal {
            maxVal = val
        }
        if val < minVal {
            minVal = val
    }
    // 将[minVal, maxVal)区间的整数数量统计到计数器中
    count := countInRange(nums[:n], minVal, maxVal)
    fmt.Println("区间[%d..%d]中有%d个数字"， minVal, maxVal, count)
}

这个算法的时间复杂度为 O(n+k),其中 n 是输入的整数个数，k 是输入的最大数字。算法的主要思路是遍历每个整数，统计它落在[a..b]区间内的个数。由于每个整数只会被计算一次，所以时间复杂度为 O(n+k)。

智谱清言：

为了实现这个算法，我们可以使用线段树（Segment Tree）数据结构。线段树可以在 O(log n) 时间内回答区间查询，但是构建线段树需要 O(n log n) 时间。由于我们需要在 O(1) 时间内回答查询，因此我们需要对线段树进行预处理。

以下是使用 Go 语言实现的算法：

package main
import (
	"container/rand"
	"fmt"
	"math/rand"
	"time"
)
type Node struct {
	L []int
	R []int
}
type SegmentTree struct {
	Root *Node
}
func (s *SegmentTree) Build(nums []int, k int) {
	s.Root = &Node{
		L: make([]int, k+1),
		R: make([]int, k+1),
	}
	build := func(node *Node, nums []int, start, end int) {
		if start > end {
			return
		}
		mid := (start + end) / 2
		node.L = build(node.L, nums, start, mid)
		node.R = build(node.R, nums, mid+1, end)
		node.L[0] += node.L[1]
		node.R[0] += node.R[1]
		node.L[0] += node.R[0]
	}
	build(s.Root, nums, 0, len(nums)-1)
}
func (s *SegmentTree) Query(a, b int) int {
	return s.Root.Query(a, b)
}
func (node *Node) Query(a, b int) int {
	if node.L[0] > b {
		return 0
	}
	if node.R[0] < a {
		return 0
	}
	if a <= node.L[0] && node.L[0] <= b {
		return node.L[0]
	} else if a <= node.R[0] && node.R[0] <= b {
		return node.R[0]
	} else {
		mid := (node.L[0] + node.R[0]) / 2
		left := node.Query(a, b)
		right := node.Query(a, b)
		if left == 0 && right == 0 {
			return 0
		} else if left == 0 {
			return right
		} else if right == 0 {
			return left
		} else {
			return left + right
		}
	}
}
func main() {
	rand.Seed(time.Now().UnixNano())
	nums := make([]int, 10)
	for i := range nums {
		nums[i] = rand.Intn(100)
	}
	k := 5
	tree := &SegmentTree{}
	tree.Build(nums, k)
	a := 3
	b := 10
	fmt.Printf("Number of integers in range [%d, %d]: %d\n", a, b, tree.Query(a, b))
}

这个实现首先构建一个线段树，然后在 O(1) 时间内回答区间查询。预处理时间复杂度为 O(n log n)，查询时间复杂度为 O(1)。

通义千问：

算法流程：

1.预处理：遍历给定的 n 个整数，对于每个整数，将其存储到一个哈希表中，同时统计哈希表中每个区间的元素个数。这里需要用到两个哈希表，一个用于存储每个整数，另一个用于存储每个区间的元素个数。预处理时间为 O(n+k)。

2.查询：对于输入的 n 个整数中落在区间[a..b]内的整数个数，可以通过以下步骤求得： a. 计算区间左右端点在哈希表中对应的区间数量，即区间 [a..b] 在哈希表中的索引范围。 b. 遍历区间 [a..b] 内的所有整数，对于每个整数，如果其在哈希表中存在，则将对应区间的元素个数加一。 c. 返回区间 [a..b] 内元素个数的总和。

时间复杂度：

预处理时间为 O(n+k)，查询时间为 O(1)。

参考代码：

天工：

可以使用线段树来解决这个问题。线段树是一种二叉树数据结构，每个节点表示一个区间。每个节点有两个子节点，分别表示该区间的左半部分和右半部分。通过构建一棵线段树，我们可以在 O(log n) 的时间内查询一个点是否在某个区间内。

具体实现如下：

1.构建线段树：对于每个节点，我们可以使用数组来存储它代表的区间内的所有整数。然后递归构建左子树和右子树，直到每个叶子节点都只有一个整数。

2.预处理：对于每个区间 [a, b]，我们需要查询它内部有多少个整数。我们可以从线段树的根节点开始遍历，如果当前节点表示的区间完全包含在 [a, b] 内，则将该区间内的整数数量加入答案中。然后递归遍历左子树和右子树，继续查询子区间内的整数数量。

3.查询：对于一个查询点 x，我们从根节点开始遍历线段树，如果 x 在当前节点表示的区间内，则将该区间内的整数数量加入答案中。然后递归遍历左子树和右子树，继续查询子区间内的整数数量。

预处理时间复杂度为 O(n+k)，其中 n 是输入的整数数量，k 是整数的范围。查询时间复杂度为 O(log n)。

chatgpt：

以下是一个使用Go语言设计的算法，能够在O(1)时间内回答输入的n个整数中有多少个落在区间[a..b]内，并具有O(n+k)的预处理时间复杂度。

package main

import (
	"fmt"
)

type PreprocessedData struct {
	prefixSum []int
}

func preprocessData(arr []int, k int) PreprocessedData {
	count := make([]int, k+1)
	prefixSum := make([]int, k+1)

	for _, num := range arr {
		count[num]++
	}

	prefixSum[0] = count[0]
	for i := 1; i <= k; i++ {
		prefixSum[i] = prefixSum[i-1] + count[i]
	}

	return PreprocessedData{
		prefixSum: prefixSum,
	}
}

func countInRange(data PreprocessedData, a, b int) int {
	if a == 0 {
		return data.prefixSum[b]
	}

	return data.prefixSum[b] - data.prefixSum[a-1]
}

func main() {
	arr := []int{1, 2, 3, 4, 5, 6, 7, 8, 9, 0}
	k := 9
	a := 2
	b := 6

	preprocessedData := preprocessData(arr, k)
	count := countInRange(preprocessedData, a, b)
	fmt.Printf("Count of numbers in range [%d, %d]: %d\n", a, b, count)
}

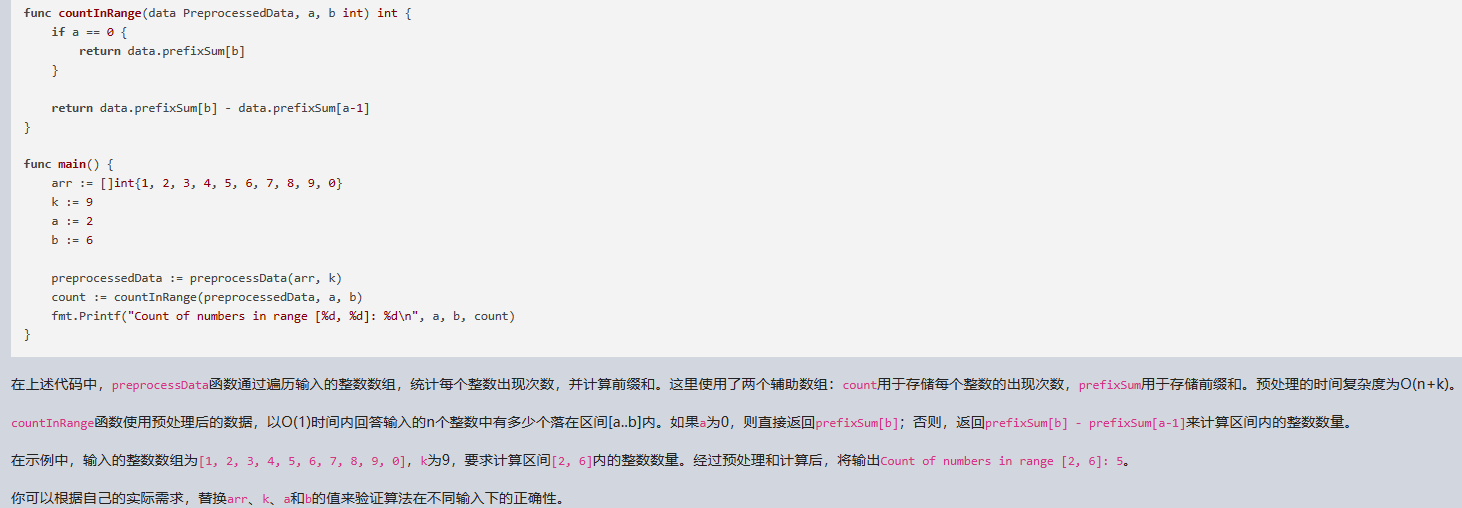
在上述代码中，preprocessData函数通过遍历输入的整数数组，统计每个整数出现次数，并计算前缀和。这里使用了两个辅助数组：count用于存储每个整数的出现次数，prefixSum用于存储前缀和。预处理的时间复杂度为O(n+k)。

countInRange函数使用预处理后的数据，以O(1)时间内回答输入的n个整数中有多少个落在区间[a..b]内。如果a为0，则直接返回prefixSum[b]；否则，返回prefixSum[b] - prefixSum[a-1]来计算区间内的整数数量。

在示例中，输入的整数数组为[1, 2, 3, 4, 5, 6, 7, 8, 9, 0]，k为9，要求计算区间[2, 6]内的整数数量。经过预处理和计算后，将输出Count of numbers in range [2, 6]: 5。

你可以根据自己的实际需求，替换arr、k、a和b的值来验证算法在不同输入下的正确性。