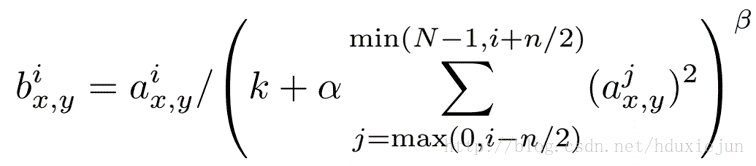在AlexNet中LRN 局部响应归一化的理
在AlexNet中LRN 局部响应归一化的理
一、LRN技术介绍:
Local Response Normalization(LRN)技术主要是深度学习训练时的一种提高准确度的技术方法。其中caffe、tensorflow等里面是很常见的方法,其跟激活函数是有区别的,LRN一般是在激活、池化后进行的一种处理方法。LRN归一化技术首次在AlexNet模型中提出这个概念。
AlexNet将LeNet的思想发扬光大,把CNN的基本原理应用到了很深很宽的网络中。AlexNet主要使用到的新技术点如下。
(1)成功使用ReLU作为CNN的激活函数,并验证其效果在较深的网络超过了Sigmoid,成功解决了Sigmoid在网络较深时的梯度弥散问题。虽然ReLU激活函数在很久之前就被提出了,但是直到AlexNet的出现才将其发扬光大。
(2)训练时使用Dropout随机忽略一部分神经元,以避免模型过拟合。Dropout虽有单独的论文论述,但是AlexNet将其实用化,通过实践证实了它的效果。在AlexNet中主要是最后几个全连接层使用了Dropout。
(3)在CNN中使用重叠的最大池化。此前CNN中普遍使用平均池化,AlexNet全部使用最大池化,避免平均池化的模糊化效果。并且AlexNet中提出让步长比池化核的尺寸小,这样池化层的输出之间会有重叠和覆盖,提升了特征的丰富性。
(4)提出了LRN层,对局部神经元的活动创建竞争机制,使得其中响应比较大的值变得相对更大,并抑制其他反馈较小的神经元,增强了模型的泛化能力。
二、为什么要有局部相应归一化(Local Response Normalization)?
三、LRN计算公式的介绍
Hinton在2012年的Alexnet网络中给出其具体的计算公式如下:
这个公式中的a表示卷积层(包括卷积操作和池化操作)后的输出结果,这个输出结果的结构是一个四维数组[batch,height,width,channel],这里可以简单解释一下,batch就是批次数(每一批为一张图片),height就是图片高度,width就是图片宽度,channel就是通道数可以理解成一批图片中的某一个图片经过卷积操作后输出的神经元个数(或是理解成处理后的图片深度)。ai(x,y)表示在这个输出结构中的一个位置[a,b,c,d],可以理解成在某一张图中的某一个通道下的某个高度和某个宽度位置的点,即第a张图的第d个通道下的高度为b宽度为c的点。论文公式中的N表示通道数(channel)。a,n/2,k,α,β分别表示函数中的input,depth_radius,bias,alpha,beta,其中n/2,k,α,β都是自定义的,特别注意一下∑叠加的方向是沿着通道方向的,即每个点值的平方和是沿着a中的第3维channel方向的,也就是一个点同方向的前面n/2个通道(最小为第0个通道)和后n/2个通道(最大为第d-1个通道)的点的平方和(共n+1个点)。而函数的英文注解中也说明了把input当成是d个3维的矩阵,说白了就是把input的通道数当作3维矩阵的个数,叠加的方向也是在通道方向。
公式看上去比较复杂,但理解起来非常简单。i表示第i个核在位置(x,y)运用激活函数ReLU后的输出,n是同一位置上临近的kernal map的数目,N是kernal的总数。参数K,n,alpha,belta都是超参数,一般设置k=2,n=5,aloha=1*e-4,beta=0.75。
整理参考文章:
在AlexNet中LRN 局部响应归一化的理的更多相关文章
- 深度学习原理与框架-Tensorflow卷积神经网络-cifar10图片分类(代码) 1.tf.nn.lrn(局部响应归一化操作) 2.random.sample(在列表中随机选值) 3.tf.one_hot(对标签进行one_hot编码)
1.tf.nn.lrn(pool_h1, 4, bias=1.0, alpha=0.001/9.0, beta=0.75) # 局部响应归一化,使用相同位置的前后的filter进行响应归一化操作 参数 ...
- 局部响应归一化(Local Response Normalization,LRN)
版权声明:本文为博主原创文章,欢迎转载,注明地址. https://blog.csdn.net/program_developer/article/details/79430119 一.LRN技术介 ...
- Fragment中onActivityResult不响应
开发中遇到Fragment中onActivityResult不响应的问题,曾经见过. 不少同学说处理方法是在与Fragment绑定的FragmentActivity中重写onActivityResul ...
- theano 实现图像局部对比度归一化
很多时候我们需要对图像进行局部对比度归一化,比如分块CNN的预处理阶段.theano对此提供了一些比较方便的操作. 局部归一化的一种简单形式为: 其中μ和σ分别为局部(例如3x3的小块)的均值和标准差 ...
- OpenCV中Mat的列向量归一化
OpenCV中Mat的列向量归一化 http://blog.csdn.net/shaoxiaohu1/article/details/8287528 OpenCV中Mat的列向量归一化 标签: Ope ...
- “全栈2019”Java第九十七章:在方法中访问局部内部类成员详解
难度 初级 学习时间 10分钟 适合人群 零基础 开发语言 Java 开发环境 JDK v11 IntelliJ IDEA v2018.3 文章原文链接 "全栈2019"Java第 ...
- Node+Express中请求和响应对象
在用 Express 构建 Web 服务器时,大部分工作都是从请求对象开始,到响应对象终止. url的组成: 协议协议确定如何传输请求.我们主要是处理 http 和 https.其他常见的协议还有 f ...
- GridView在PopWindow中OnItemClick不响应
在安卓4.0系统中,GridView在PopWindow中OnItemClick不响应,但是有按压效果.需要PopWindow的Show时加入这行代码: popupWindow.setFocusabl ...
- 3D场景中的鼠标响应事件
原文:3D场景中的鼠标响应事件 今天要讲的是3D场景中的鼠标响应事件的处理,首先Button的响应是大家熟知的,只要加上一个click事件,然后写一个响应的处理时间就行了.对于二维平面上的一些控件也很 ...
随机推荐
- Windows中的"簇"和Linux中的"块"是对应的
扇区是对硬盘而言,块是对文件系统而言. 簇”又称为“分配单元” ,文件系统是操作系统与驱动器之间的接口,当操作系统请求从硬盘里读取一个文件时,会请求相应的文件系统(FAT 16/32/NTFS)打开文 ...
- arc098E Range Minimum Queries
题意:给你一个n个数的数组,每次能够选取连续的长度为K的子序列,取出其中任意一个最小元素. 一共操作Q次.问取出的元素中Max-Min最小是多少? 标程: #include<bits/stdc+ ...
- leetcode-157周赛-5215黄金矿工
题目描述: 方法一:dfs class Solution: def getMaximumGold(self, grid: List[List[int]]) -> int: maxx = 0 R, ...
- Jmeter-BeanShell断言:将数据库结果封装成list作为参数
import com.alibaba.fastjson.JSON; import com.alibaba.fastjson.JSONObject; import com.alibaba.fastjso ...
- day34 反射、面向对象内置方法:如__str__、面向对象的软件开发
Python之路,Day21 = 反射.面向对象内置方法:如__str__.面向对象的软件开发 几个内置查看的方法使用 .__base__ 查看类的继承结构.mro() 对象找属性的顺序存在里面 -- ...
- 学习Caffe(一)使用Caffe
如何使用Caffe Caffe教程(http://robots.princeton.edu/courses/COS598/2015sp/slides/Caffe/caffe_tutorial.pdf) ...
- DNS的解析过程
1.什么是DNS 在互联网上,唯一标识一台计算机的是IP地址,但是IP地址不方便记忆,通过一个域名对应一个IP地址,来达到找到IP地址的目的,那么DNS就是将域名转换成IP地址的过程. 2.DNS查询 ...
- win7防火墙里开启端口的图文教程 + SNMP测试感触
转:http://www.cnblogs.com/vipsoft/archive/2012/05/02/2478847.html 开启端口:打开“控制面板”中的“Windows防火墙”,点击左侧的“高 ...
- pinmap 和 pin allocation
串口管脚分配
- nginx下Thinkphp 隐藏index.php
thinkphp config配置: 'URL_MODEL' => '2', //URL模式 nginx rewrite配置: location / { if (!-e $request_fil ...