LeetCode.509——斐波那契数

---

• 问题描述：

  斐波那契数，通常用 F(n) 表示，形成的序列称为斐波那契数列。该数列由 0 和 1 开始，后面的每一项数字都是前面两项数字的和。也就是：

  F(0) = 0,   F(1) = 1
  F(N) = F(N - 1) + F(N - 2), 其中 N > 1.
  

  给定 N，计算 F(N)。

  示例 ：

  输入：2
  输出：1
  解释：F(2) = F(1) + F(0) = 1 + 0 = 1.
  

• 问题分析：

  由于计算任何一个第n(n >= 2)项的数都需要知道其前面两个数，即需要知道n-1和n-2是多少，然后两个相加得到结果，但是问题来了，要知道n-1，就要需要知道n-2，要知道n-2就需要知道n-3，会一直这样的循环递归下去，一直到第一个数，第二个，第三个.......再反推回来。 那就很明显了，大家第一时间想到的方法便是递归，就下来实现一下：

  方法一：递归实现

  public class Solution {
  	 public int fib(int n) {
       	if(n <= 1){
              return n;
          }
           return fib(n-1) + fib(n-2);
       }
  }
  

​ 问题分析：

​ 先看一下递归图：

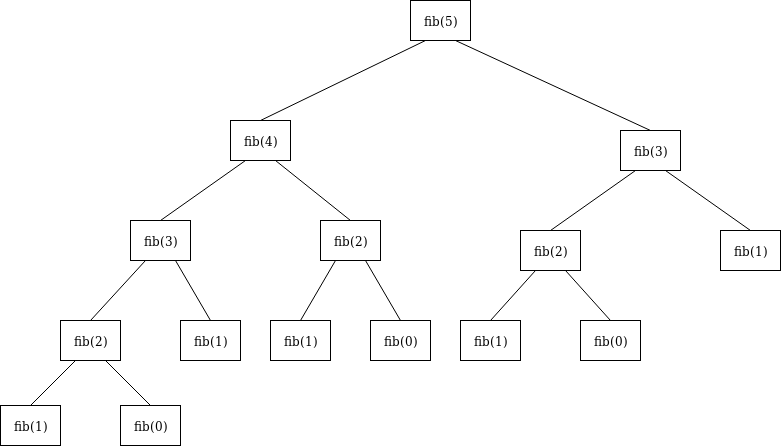
​ 由于很多数的计算都要重复很多次，效率并不高，时间复杂度达到了 O（2^n），是斐波那契数计算中 时间复杂度最大，最不可取的方法。

​ 空间复杂度：O（n）,堆栈中需要的空间与 N 成正比，堆栈会跟踪 fib(n) 的调用，随着堆栈的不断增长 如果没有足够的内存则会出现StackOverflowError异常。

​ 注：定义为int型时，最大只能求到n = 46，f(46) = 1836311903, 而 f(47) = -1323752223,因为超出了int 型数值的最大范围。

• 算法改进：

  使用递归的同时，使用记忆化方式存储已经计算过的数据，减少不必要的重复计算，可以使时间复杂度降到 O(N),同时空间复杂度也是O(N)。具体的实现是使用一个数组，把每次计算过的值都存储进去，当再次使用这个数的时候，直接返回，不需要再进行递归。

  方法二：记忆化自底向上递归

  public class Solution {
  	 public int fib(int n) {
       	if(n <= 1){
              return n;
          }
           int[] memo = new int[n+1];
           memo[1] = 1;
           for(int i = 2;i <= n; i++){
               //自底向上填充数组，一直到需要的那个数
               memo[i] = memo[i-1] + memo[i-2];
           }
           return memo[n];
       }
  }
  

方法三：使用第三方变量

class Solution {
    public int fib(int N) {
        if (N < 2) return N;
        if (N == 2) return 1;

        int temp = 1;
        int result = 1;
        for (int i = 3; i <= N ; i++) {
            result= temp + result;
            temp = result - temp;
        }
        return result;
    }
}

时间复杂度瞬间降到O(1)，这个我觉得应该是三个方法里面最简单最高效的。

---

• 最后：

  限于水平有限，斐波那契数的实现还有很多种方法，不能一一列举，当其中大部分都有类似的思想。

  水文中如有不准确或是错误之处，还望指出。谢谢~~~

  下一篇：LeetCode.62——不同路径