cocos2dx Quaternion 四元数(1/2)

这篇文章只是我学完四元数之后的一些理解，其实是对别人理解的理解，有些地方我理解但是没有写下来，如果真的想深入的学习四元数，建议从学习复数开始。

这个知识点需要几何想象的天赋和学习的耐心，缺一不可，慢慢啃不要急躁。

推荐几个学习的视频

1. b站的四元数讲解 四元数的可视化
2. 接上第二集四元数的可视化2
3. 四元数的演示上面视频里的四元数交互图

第一个视频讲原理多一些，第二个视频会说一些旋转的具体计算，但你不看第一个肯定看不懂第二个【笑

在下面会简单的介绍一些原理和解析方面的东西，但是很多等式没有列出，需要再查找别的资料来学习。

这是一个四元数在三维上的投影，他的方程如下

（其实原方程应该表示为p=w+xi+yj+zk 四维坐标就是(w, x, y, z)



我们可以看到x轴为1，在图上也有显示

在这个方程中我们需要知道的是：

1. x²+y²+z²=1
2. p是想要旋转的点，q是旋转的轴
3. ijk前面的数字表示的是xyz轴
4. 加号前面实部和后面的虚部分别用余弦和正弦来表示
5. 旋转的角度在这里代入时使用的是半角，为什么是半角在后面解释
6. ij=-ji=k, jk=-kj=i, ki=-ik=j ，这个也需要解释一下

在解释第四个问题之前还需要了解一个知识叫做：左乘右手定则，右乘左手定则。

根据图一我们可以知道ijk轴互相垂直，如果是ij=k，我们想让j轴上的点旋转90度，可以理解为i推动j变成了k，左乘用右手定则，让大拇指指向i的正轴，握住i轴按照剩下四指方向旋转90度，是不是将j轴上的点旋转到了k轴上了。

这个是右手定则，左手定则是右乘的时候使用的。

还是按照上面例子里的式子，ij=k，还是旋转90度，j右乘i得到k，使用左手，大拇指朝向j轴正方向，旋转90度，将i轴上的点旋转到了k轴上了。

按照左右手定则再结合球极投影，可以很快的记住是怎么旋转的。

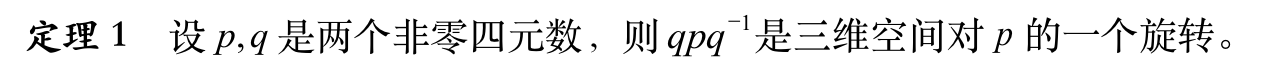
四元数的有个定理，如上，所以我们知道可以如何旋转一个三维空间上的点，要解释为什么在旋转时使用半角，还需要解释为什么使用要qpq-1中为什么乘了一个四元数的共轭。

将其先进行P变化使其映射到新空间的另一个点

而这个点同一个线性变换时的矩阵是A然后再通过P逆使其映射回之前的空间

在这篇文章中解释了为什么要变换

简单的说qp相乘之后p被拉到了四维空间中，为了让它能在三维空间中表示，乘以q逆将它拉回到三维空间中来，不知道这么解释对不对，我是这么理解的。qp之后p中的实部被转移到了虚部，为了让它回到实部，在乘以q逆可以将虚部转移到实部。

而半角就是因为旋转了两次，qp旋转了一次这是按照正轴旋转的，用右手定则来旋转，第二次旋转是(q*p)*q-1，是按照负轴来旋转的，用左手定则，由于是四元数的逆，所以虽然是用左手定则来旋转，但是和之前旋转的方向是一样的。

所以这里使用半角的原因就是前后一共旋转了两次。

右乘四元数的逆是为了降维。

半角是为了解决共轭方向第二次旋转的问题。

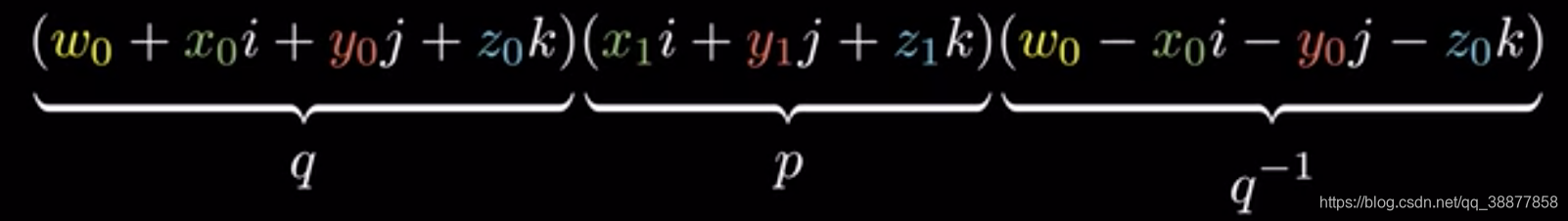
看到这其实大部分代码就已经能看懂了，下一篇写cocos2dx的代码注释。