纪中10日T1 2300. 【noip普及组第一题】模板题

2300. 【noip普及组第一题】模板题

(File IO): input:template.in output:template.out

时间限制: 1000 ms  空间限制: 262144 KB  具体限制

题目描述

输入

输出

样例输入

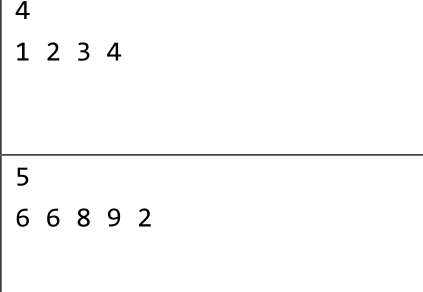
样例输出

数据范围限制

朴素算法

考试开始的前一个小时我一直在折腾朴素算法 -> 对拍

 #pragma GCC optimize(2)
 #include<bits/stdc++.h>
 #define IL inline
 using namespace std;
 int a[];
 bool vis[];
 int n,k,maxans;
 bool cmp(int a,int b)
 {
     return a>b;
 }
 int gcd(int a,int b)
 {
     if(b==) return a;
     if(b==) return ;
     if(a%==&&b%==) return *gcd(a/,b/);
     if(a%==&&b%==) return gcd(a,b/);
     if(a%==&&b%==) return gcd(a/,b);
     if(a%==&&b%==) return gcd(b,a%b);
 //    return (b==0)?a:gcd(b,a%b);
 //这里还用到了二进制gcd（会更快一点）
 }
 void search(int depth/*k*/,int now)
 {
     if(depth==k) {
         maxans=max(maxans,now);
         return;
     }
     int maxgcd=,maxnum=;
     for(int i=;i<=n;i++)
     {
         if(vis[i]) continue;
         if(gcd(now,a[i])>maxgcd){
             maxnum=i;
             maxgcd=gcd(now,a[i]);
             if(depth+<k){
                 vis[i]=;
                 search(depth+,maxgcd);
                 vis[i]=;
             }
         }
         if(depth+==k)
         {
             vis[i]=;
             search(depth+,maxgcd);
             vis[i]=;
         }
     }
 }
 int main()
 {
     freopen("template.in","r",stdin);
     freopen("template.out","w",stdout);
     cin>>n;
     for(int i=;i<=n;i++)
         scanf("%d",a+i);
     sort(a+,a+n+,cmp);
     for(k=;k<=n;k++)
     {
         if(a[k]==){
             printf("1\n");
             continue;
         }
         maxans=;
         for(int s=;s<=n;s++)
         {
             vis[s]=;
             search(,a[s]);
             vis[s]=;
         }
         printf("%d\n",maxans);
     }
     return ;
 }

我再也不想看到了

这个算法就是模拟，谁都会写吧？

O（n²）算法

我会写出这个算法来，完全是因为下面的那一种在考试时我写出来有问题

Solution

先在输入的同时预处理出每个数的所有因数（可以是质数，合数，也可以是1）

for(int j=;j<a;j++)
    if(a%j==)
        array[j]++;

这样子的好处是，我没有保存每一个数，而是统计了所有的因子

这里的array[i]就表示因子有i的数有多少个

于是我们要计算 10,000个数 * 10,000个可能的因子 次询问

哈哈

还是把这种讲完吧

然后再外层循环k++

内层循环i--

一旦有一个array[i]>=k

就把这时的i输出即可

Code（TLE70分）

 //#pragma GCC optimize(2)
 #include<bits/stdc++.h>
 using namespace std;
 int array[];
 int a,n,k,maxa;
 int main()
 {
     freopen("template.in","r",stdin);
     freopen("template.out","w",stdout);
     cin>>n;
     for(int i=;i<=n;i++){
         scanf("%d",&a);
                 for(int j=;j<a;j++)
                         if(a%j==)
                 array[j]++;
                 maxa=max(maxa,a);
     }
     int b=maxa;
     for(k=;k<=n;k++)
     {
         for(int i=b;i>;i--)
         {
             if(array[i]>=k){
                 cout<<i<<endl;
                 b=i;
                 break;
             }
         }
     }
     return ;
 }

Code（TLE70分）

O（n sqrt（n））算法

Solution