洛谷 P3374 【模板】树状数组 1 题解

P3374 【模板】树状数组 1

题目描述

如题，已知一个数列，你需要进行下面两种操作：

1.将某一个数加上x

2.求出某区间每一个数的和

输入格式

第一行包含两个整数N、M，分别表示该数列数字的个数和操作的总个数。

第二行包含N个用空格分隔的整数，其中第i个数字表示数列第i项的初始值。

接下来M行每行包含3个整数，表示一个操作，具体如下：

操作1： 格式：1 x k 含义：将第x个数加上k

操作2： 格式：2 x y 含义：输出区间[x,y]内每个数的和

输出格式

输出包含若干行整数，即为所有操作2的结果。

输入输出样例

输入 #1

5 5

1 5 4 2 3

1 1 3

2 2 5

1 3 -1

1 4 2

2 1 4

输出 #1

14

16

说明/提示

时空限制：1000ms,128M

数据规模：

对于30%的数据：N<=8，M<=10

对于70%的数据：N<=10000，M<=10000

对于100%的数据：N<=500000，M<=500000

样例说明：

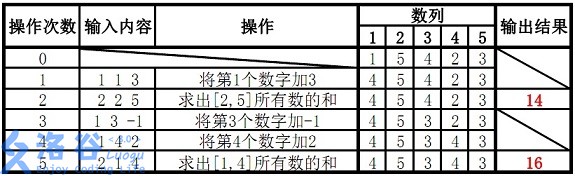
故输出结果14、16

【思路】

之前做过现在是拿出来复习一下，没想到由于太久不写导致生疏到什么东西都忘掉了。。

只能重学树状数组

详细的讲解很多题解和博客都写得很好了，

所以我只在这里说一下易错或者难懂的地方

【题目大意】

单点修改，区间查询

【树状数组复杂度】

树状数组的查询和修改的复杂度都是最坏情况nlogn

比线段树要少而且比普通数组要好写

【什么是lowbit】

lowbit求的是这个数在二进制的情况下最低位的1表示的数

比如6：

先转化为二进制—— 110

最低位的1表示的数就是10,

转化为十进制就是2

【lowbit有什么用】

知道了一个数的lowbit这个数修改之后会影响的数是哪一个

感性理解一下就好

还是比如6：

lowbit(6) = 2,

所以修改了6之后会影响的下一个数就是6 + 2 = 8

然后8在继续影响8 + lowbit(8) 之后的数

直达到达n

【求1-i的值】

也就是下面代码中sum函数的作用

求出1-i的值

因为a[i]代表的不一定是i位置的数

还有可能是和前面的某些数数加起来的和

所以要不重复的找出1-i中的某些a[i]

使他们代表的数刚好是不重复而且不少的出现1-i中的每一个数

减去lowbit就是跳过那些它包括的数

感性理解一下就好

【完整代码】

#include<iostream>
#include<cstdio>
#define int long long

using namespace std;

int read()
{
	int sum = 0,fg = 1;
	char c = getchar();
	while(c < '0' || c > '9'){if(c == '-')fg = -1;c = getchar();}
	while(c >= '0' && c <= '9'){sum = sum * 10 + c - '0';c = getchar();}
	return sum * fg;
}
const int Max = 500005;
int a[Max];
int n,m;

int lowbit(int x)
{
	return x & -x;
}

void add(int x,int y)
{
	while(x <= n)
	{
		a[x] += y;
		x += lowbit(x);
	}
}

int sum(int x)
{
	int ans = 0;
	while(x > 0)
	{
		ans += a[x];
		x -= lowbit(x);
	}
	return ans;
}

signed main()
{
	n = read(),m = read();
	for(register int i = 1;i <= n;++ i)
	{
		int qwq = read();
		add(i,qwq);
	}
	for(register int i = 1;i <= m;++ i)
	{
		int x = read(),y = read(),z = read();
		if(x == 1)
			add(y,z);
		else
			cout << sum(z) - sum(y - 1) << endl;
	}
	return 0;
}