单变量微积分笔记20——三角替换1（sin和cos）

sin和cos的常用公式

　　基本公式：

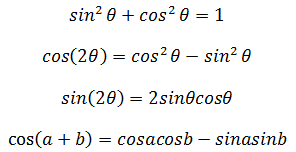
　　半角公式：

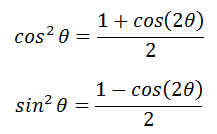
　　微分公式：

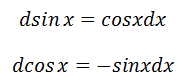
　　积分公式：

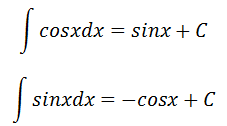
三角替换

示例1

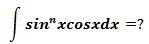
　　根据微分公式，cosxdx = dsinx

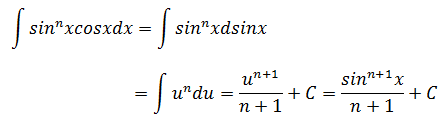
示例2

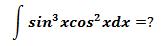
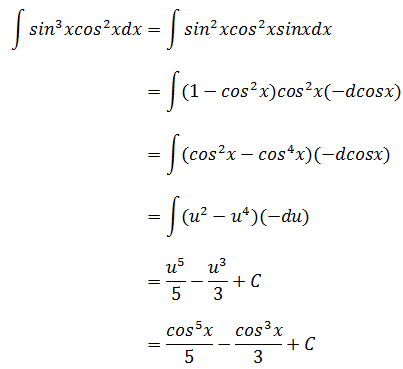
示例3

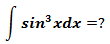
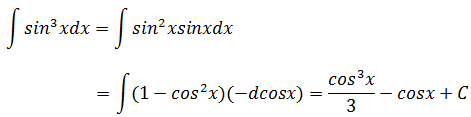
半角公式

示例1

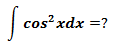
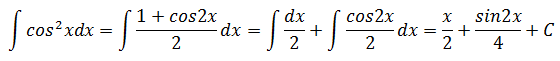
示例2

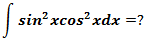
　　解法1：

　　解法2：

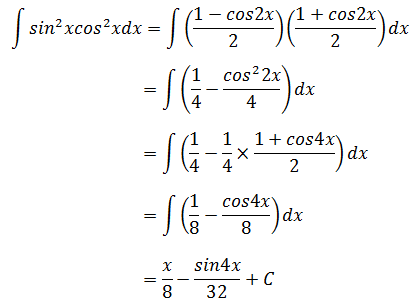
综合示例

示例1

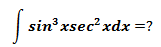
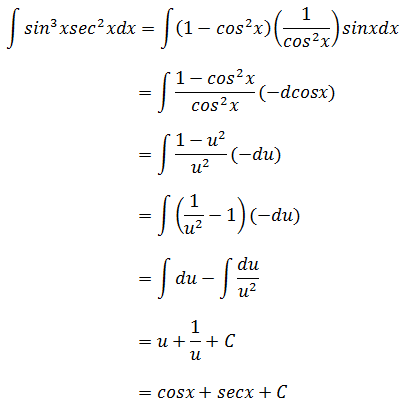
示例2

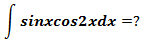
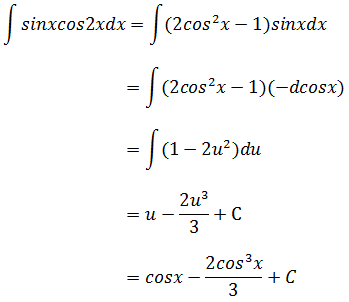
示例3

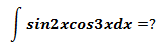
　　三角函数和x的倍数都不一样，我们的目标是将x的倍数和三角函数转换为一致。

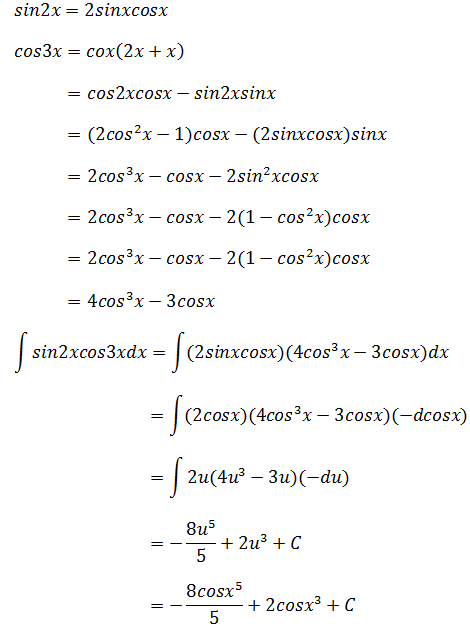
示例4

　　y = sin(ax)绕x轴旋转一周，ax的定义域是[0, π]，求旋转后图形的体积。

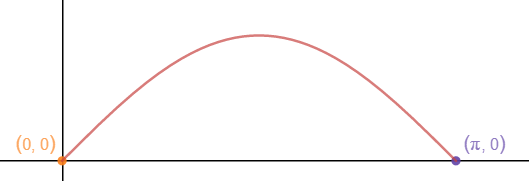
　　根据圆盘法（圆盘法参见数学笔记17——定积分的应用2（体积））：

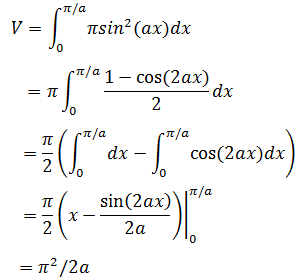
　　解法2：

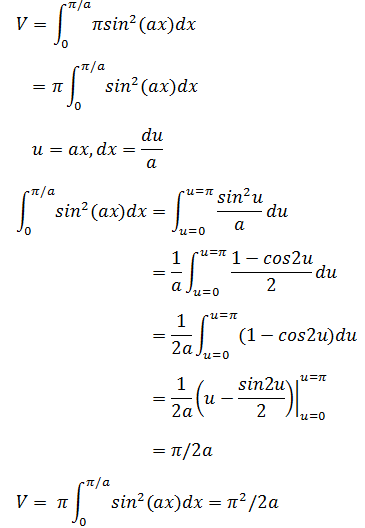
示例5

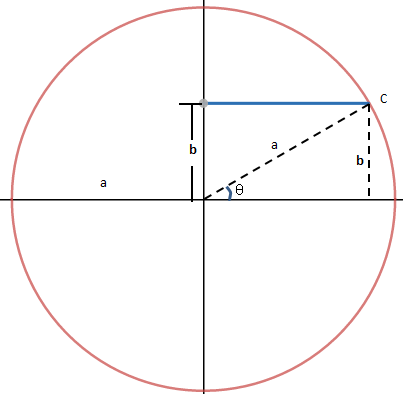
　　如下图所示，已知圆的半径a和线段长度b，求阴影部分的面积。

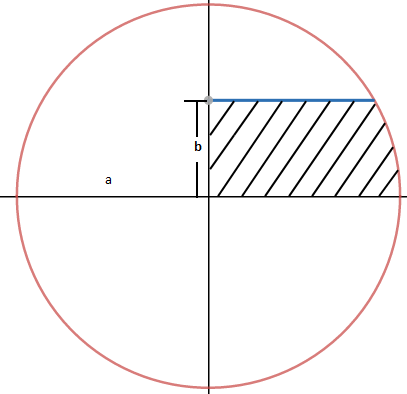
　　解法1，使用中学数学的知识，引一条与圆交于C点的辅助线，所求面积就变成了三角形的面积S₁与扇形的面积S₂之和，如下图所示：

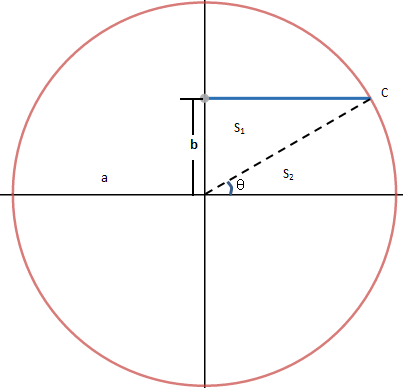
　　通过圆的公式x² + y² = a²，可知C的坐标是。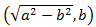

　　将上图映射到极坐标，则x = acosθ，y = asinθ，在C点，y = b = asinθ，θ = arcsin(b/a)

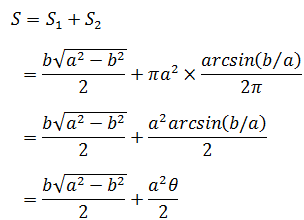
　　解法2，使用定积分直接求解，面积是：

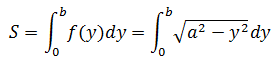
　　 现在的问题变成了如何求解定积分。

　　如上图所示，与解法1一样引入极坐标，x = acosθ，y = asinθ，将θ写成关于y的函数，θ = arcsin(y/a)

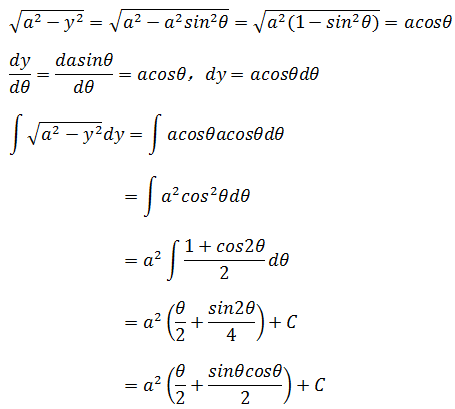
　　现在已经求得原函数，最后一步是求解定积分。可以将积分上下限替换成θ的表达式，也可将原函数的θ用y表示，这里使用第二种：

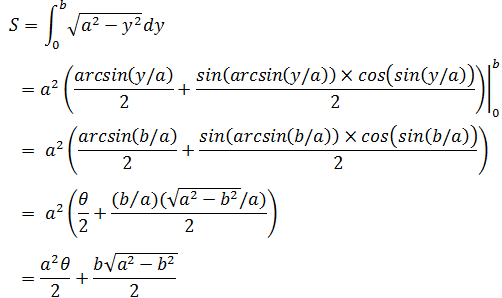
　　看起来积分并不是每次都能使问题简单，虽然得到了一个方便的表达式，但这个表达式求解起来可能很困难。

---

　　作者：我是8位的

　　出处：http://www.cnblogs.com/bigmonkey

　　本文以学习、研究和分享为主，如需转载，请联系本人，标明作者和出处，非商业用途！