隐马尔可夫模型(HMM)及Viterbi算法

HMM简介

　　对于算法爱好者来说，隐马尔可夫模型的大名那是如雷贯耳。那么，这个模型到底长什么样？具体的原理又是什么呢？有什么具体的应用场景呢？本文将会解答这些疑惑。
　　本文将通过具体形象的例子来引入该模型，并深入探究隐马尔可夫模型及Viterbi算法，希望能对大家有所启发。
　　隐马尔可夫模型（HMM，hidden Markov model）是可用于标注问题的统计学模型，描述由隐藏的马尔可夫链随机生成观测序列的过程，属于生成模型。HMM模型在实际的生活和生产中有着广泛的应用，包括语音识别，自然语言处理，生物信息，模式识别等领域。

引入

　　某天，你的女神告诉你说，她放假三天，将要去上海游玩，准备去欢乐谷、迪士尼和外滩（不一定三个都会去）。
　　她呢，会选择在这三个地方中的某几个逗留并决定是否购物，而且每天只待在一个地方。根据你对她的了解，知道她去哪个地方，仅取决于她去的上一个地方，且是否购物的概率仅取决于她去的地方。已知她去的三个地方的转移概率表如下：

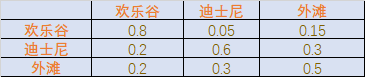
稍微对这个表格做些说明，比如第一行，前一天去了欢乐谷后，第二天还待在欢乐谷的概率为0.8，去迪士尼的概率为0.05，去外滩的概率为0.15。
她在每个地方的购物概率为：

地点	购物概率
欢乐谷	0.1
迪士尼	0.8
外滩	0.3

在出发的时候，她跟你说去每个地方的可能性相同。后来，放假回来后，你看了她的朋友圈，发现她的购物情况如下：第一天不购物，第二三天都购物了。于是，你很好奇，她这三天都去了哪些地方。
怎么样，聪明的你能求解出来吗？

HMM的模型参数

　　接下来，我们将会介绍隐马尔可夫模型（HMM）。
隐马尔可夫模型是关于时序的概率模型，描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列，再由各个状态生成一个观测而产生观测随机序列的过程。隐藏的马尔可夫链随机生成的状态的序列，称为状态序列；每个状态生成一个观测，而由此产生的观测的随机序列，称为观测序列。序列的每一个位置又可以看作是一个时刻。
隐马尔可夫模型由初始概率分布、状态转移概率分布以及观测概率分布确定。隐马尔可夫模型的形式定义如下：
设Q是所有可能的状态的集合，V是所有可能的观测的集合，也就是说，Q是不可见的，而V是可见的，是我们观测到的可能结果。

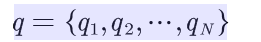
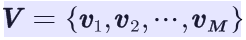
其中，N是可能的状态数，M是可能的观测数。
在刚才的例子中，Q是不可见的状态集合，应为，而V是可以观测的集合，应为V={购物，不购物}。
I是长度为T的状态序列，O是对应的观测序列。

在刚才的例子中，I这个序列是我们需要求解的，即女生去了哪些地方，而O是你知道的序列，O={不购物，购物，购物}。
A是状态转移概率矩阵：

其中，

是在时刻t处于状态q_i的条件下在时刻t+1转移到状态q_j的概率。在刚才的例子中，转移概率矩阵为：

B是观测概率矩阵：

其中，

是在时刻t处于状态q_j的条件下生成观测v_k的概率。在刚才的例子中：

是初始状态概率向量,其中是时刻t=1处于状态q_j的概率。在刚才的例子中，

综上，我们已经讲完HMM中的基本概念。同时，我们可以知道，隐马尔可夫模型由初始状态概率向量，状态转移概率矩阵A，和观测概率矩阵B决定。和A决定状态序列，B决定观测序列。因此，隐马尔可夫模型可用三元符号表示，即

称为HMM的三要素。

当然，隐马尔可夫模型之所以被称为马尔可夫模型，是因为它使用了两个基本的假设，其中之一为马尔可夫假设。它们分别是：

齐次马尔科夫假设，即假设隐藏的马尔可夫链在任意时刻t的状态只依赖于其前一时刻的状态，与其他时刻的状态及观测无关，也与时刻t无关。

观测独立性假设，即假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态，与其他观测及状态无关。

在刚才的假设中，我们对应的两个假设分别为：她去哪个地方，仅取决于她去的上一个地方；是否购物的概率仅取决于她去的地方。前一个条件为齐次马尔科夫假设，后一个条件为观测独立性假设。
以上，我们就介绍了HMM的基本概念及假设。而HMM的三个基本问题如下：

1. 概率计算问题。给定模型和观测序列,计算在模型下观测序列O出现的概率.

2. 学习问题。已知观测序列，估计模型参数，使得在该模型下观测序列概率最大。

3. 预测问题。已知模型和观测序列，求对给定观测序列条件概率最大的状态序列即给定观测序列，求最有可能的对应的状态序列。

上面的例子即为HMM的第三个基本问题，也就是，给定观测序列{不购物，购物，购物}，结果最有可能的状态序列，即游玩的地方。

Viterbi算法

求解HMM的第三个基本问题，会用到大名鼎鼎的维特比算法（Viterbi Algorithm）。
维特比算法以安德鲁·维特比（Andrew Viterbi）命名，是现代数字通信中最常用的算法，同时也是很多自然语言处理采用的解码算法。可以毫不夸张地讲，维特比是对我们的生活影音力最大的科学家之一，因为基于CDMA的3G移动通信标准主要就是他和厄文·雅各布（Irwin Mark Jacobs）创办的高通公司（Qualcomm）指定的。
维特比算法是一个特殊但应用最广的动态规划（dynamic programming）算法，利用动态规划，可以解决任何一个图中的最短路径问题，同时，它也是求解HMM描述的第三个基本问题的算法。
在维特比算法中，需要引入两个变量和。定义在时刻t状态i的所有单个路径中概率最大值为

定义在时刻t状态为i的所有单个路径中概率最大的路径的第i-1个节点为

下面是维特比算法在HMM的第三个基本问题的算法：

Python代码实现

# -*- coding: utf-8 -*-
# HMM.py
# Using Vertibi algorithm
 
import numpy as np
 
def Viterbi(A, B, PI, V, Q, obs):
 
    N = len(Q)
    T = len(obs)
    delta = np.array([[0] * N] * T, dtype=np.float64)
    phi = np.array([[0] * N] * T, dtype=np.int64)
    # 初始化
    for i in range(N):
        delta[0, i] = PI[i]*B[i][V.index(obs[0])]
        phi[0, i] = 0
 
    # 递归计算
    for i in range(1, T):
        for j in range(N):
            tmp = [delta[i-1, k]*A[k][j] for k in range(N)]
            delta[i,j] = max(tmp) * B[j][V.index(obs[i])]
            phi[i,j] = tmp.index(max(tmp))
 
    # 最终的概率及节点
    P = max(delta[T-1, :])
    I = int(np.argmax(delta[T-1, :]))
 
    # 最优路径path
    path = [I]
    for i in reversed(range(1, T)):
        end = path[-1]
        path.append(phi[i, end])
 
    hidden_states = [Q[i] for i in reversed(path)]
 
    return P, hidden_states
 
def main():
 
    # 状态集合
    Q = ('欢乐谷', '迪士尼', '外滩')
    # 观测集合
    V = ['购物', '不购物']
    # 转移概率: Q -> Q
    A = [[0.8, 0.05, 0.15],
         [0.2, 0.6, 0.2],
         [0.2, 0.3, 0.5]
        ]
 
    # 发射概率, Q -> V
    B = [[0.1, 0.9],
         [0.8, 0.2],
         [0.3, 0.7]
         ]
 
    # 初始概率
    PI = [1/3, 1/3, 1/3]
 
    # 观测序列
    obs = ['不购物', '购物', '购物']
 
    P, hidden_states = Viterbi(A,B,PI,V,Q,obs)
    print('最大的概率为: %.5f.'%P)
    print('隐藏序列为：%s.'%hidden_states)
 
main()

输出结果如下：

最大的概率为: 0.02688.
隐藏序列为：['外滩', '迪士尼', '迪士尼'].

现在，你有很大的把握可以确定，你的女神去了外滩和迪士尼。

参考文献

一文搞懂HMM（隐马尔可夫模型）：https://www.cnblogs.com/skyme/p/4651331.html
李航《统计学习方法》清华大学出版社
HMM与分词、词性标注、命名实体识别：http://www.hankcs.com/nlp/hmm-and-segmentation-tagging-named-entity-recognition.html
Hidden Markov Models 1: http://docplayer.net/21306742-Hidden-markov-models-1.html
吴军《数学之美》人民邮电出版社