20191028 牛客网CSP-S Round2019-1
花了 \(30min\) 打了 \(180\) 分的暴力...
仓鼠的石子游戏
问题描述
链接:https://ac.nowcoder.com/acm/contest/1100/A
仓鼠和兔子被禁止玩电脑,无聊的他们跑到一块空地上,空地上有许多小石子。兔子捡了很多石子,然后将石子摆成n个圈,每个圈由a[i]个石子组成。然后兔子有两根彩色笔,一支红色一支蓝色。兔子和仓鼠轮流选择一个没有上色的石子涂上颜色,兔子每次可以选择一个还未染色的石子将其染成红色,而仓鼠每次可以选择一个还未染色的石子将其染成蓝色,并且仓鼠和兔子约定,轮流染色的过程中不能出现相邻石子同色,谁不能操作他就输了。假设他们两个都使用了最优策略来玩这个游戏,并且兔子先手,最终谁会赢得游戏?
输入格式
第一行输入一个正整数T,表示有T组测试案例。
每组测试案例的第一行输入一个n,表示有n圈石子。 第二行输入n个正整数a[i],表示每个圈的石子数量。
输出格式
对于每组测试案例,如果兔子赢了,输出”rabbit“(不含引号)如果仓鼠赢了,输出"hamster"(不含引号)。
数据规模与约定
本题共有10组测试点数据。
对于前 \(30\%\) 的数据,满足 \(n=1,1 \le a[i] \le 7,1 \le T \le 10\)
对于前 \(60\%\) 的数据,满足 \(1 \le n \le 10^3,1 \le a[i] \le 7,1 \le T \le 10^2\) 。
对于前 \(100\%\) 的数据,满足 \(1 \le n \le 10^3,1 \le a[i] \le 10^9,1 \le T \le 10^2\)。
对于测试点 \(6\) ,在满足前 \(60\%\) 的数据条件下,额外满足 \(a[i]=1\) 。
题解
发现对于每一堆来说:
偶数堆相当于没有:不能改变先后手顺序
奇数堆:只能放偶数个
\(1\)的堆:改变先后手
因此,只保留 \(1\) 个奇数堆。这个奇数堆进入时是先手的人输。
就相当于用 \(1\) 的堆改变先后手后,看谁是后手。
发现当 \(1\) 堆的数目为奇数时, rabbit 赢,否则 hamster 赢。
\(\mathrm{Code}\)
#include<bits/stdc++.h>
using namespace std;
template <typename Tp>
void read(Tp &x){
x=0;char ch=1;int fh;
while(ch!='-'&&(ch>'9'||ch<'0')) ch=getchar();
if(ch=='-') ch=getchar(),fh=-1;
else fh=1;
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
x*=fh;
}
const int maxn=1007;
int T,n,sum;
int a[maxn];
int cnt;
void reset(){
sum=cnt=0;
}
int main(){
read(T);
while(T--){
read(n);reset();
for(int i=1;i<=n;i++){
read(a[i]);
if(a[i]==1) ++sum;
else if(a[i]&1) ++cnt;
}
cnt=cnt%2;
if(cnt==0){
if(sum&1) puts("rabbit");
else puts("hamster");
}
else{
if(sum&1) puts("rabbit");
else puts("hamster");
}
}
return 0;
}
乃爱与城市的拥挤程度
问题描述

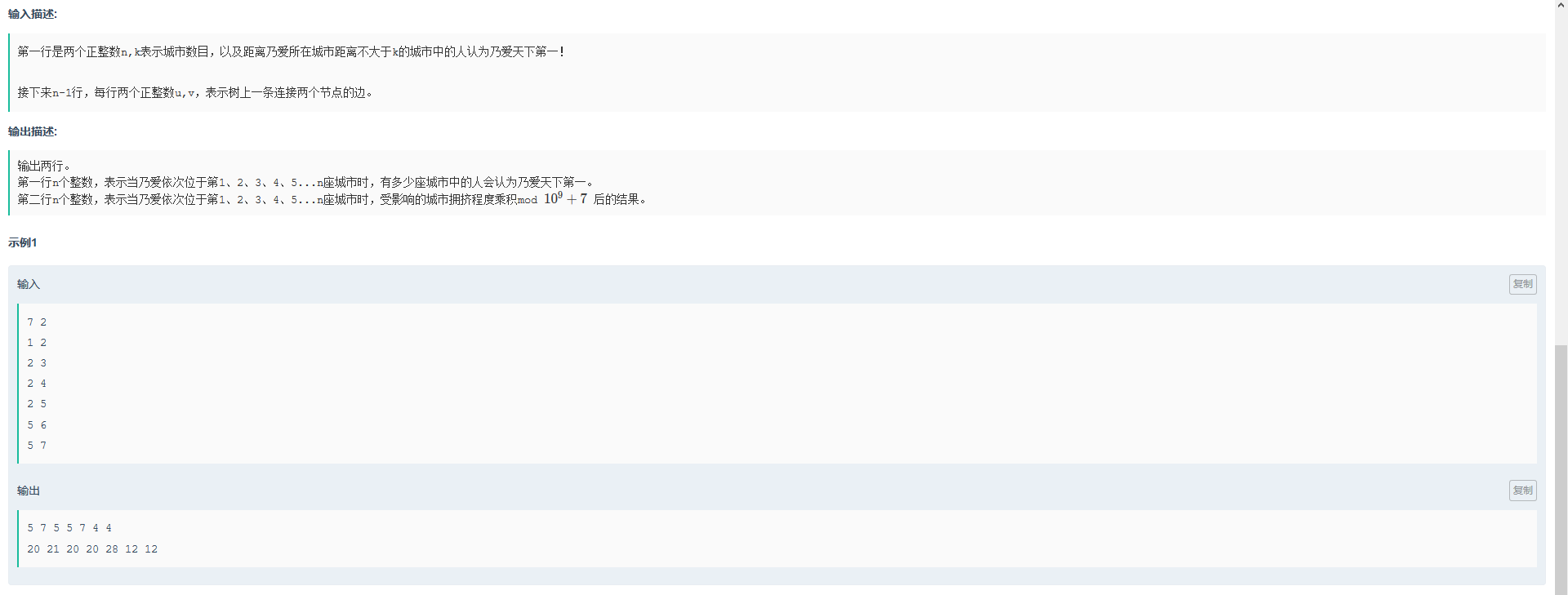

题解
\(80\%\)
随机树部分+链
直接暴力跑就完事了。
#include<bits/stdc++.h>
using namespace std;
template <typename Tp>
void read(Tp &x){
x=0;char ch=1;int fh;
while(ch!='-'&&(ch>'9'||ch<'0')) ch=getchar();
if(ch=='-') ch=getchar(),fh=-1;
else fh=1;
while(ch>='0'&&ch<='9') x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
x*=fh;
}
const int maxn=100007;
const int maxm=200007;
const int mod=1000000007;
int n,k;
int Head[maxn],to[maxm],Next[maxm],tot=1;
void add(int x,int y){
to[++tot]=y,Next[tot]=Head[x],Head[x]=tot;
}
int ans,tmp;
int aaa[maxn],bbb[maxn];
int dfs(int x,int fa,int dis){
int res=1;++ans;
if(dis==k) return res;
for(int i=Head[x];i;i=Next[i]){
int y=to[i];
if(y==fa) continue;
res+=dfs(y,x,dis+1);
}
tmp=(long long)tmp*(long long)res%mod;
return res;
}
void solve(int x){
ans=0,tmp=1;
dfs(x,0,0);
aaa[x]=ans,bbb[x]=tmp;
}
int main(){
read(n);read(k);
for(int i=1,x,y;i<n;i++){
read(x);read(y);
add(x,y);add(y,x);
}
for(int i=1;i<=n;i++){
solve(i);
}
for(int i=1;i<=n;i++){
printf("%d%c",aaa[i]," \n"[i==n]);
}
for(int i=1;i<=n;i++){
printf("%d%c",bbb[i]," \n"[i==n]);
}
return 0;
}
\(100\%\)
换根DP。
小w的魔术扑克
问题描述


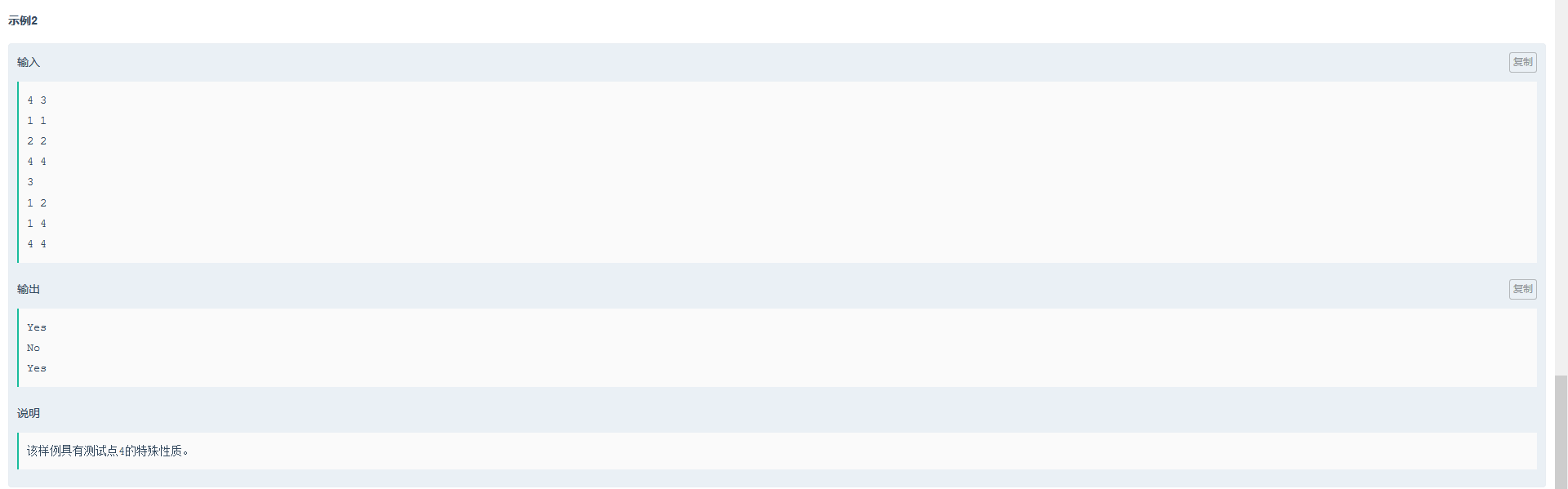

20191028 牛客网CSP-S Round2019-1的更多相关文章
- 牛客网 --java问答题
http://www.nowcoder.com/ 主要是自己什么都不怎么会.在这里可以学习很多的! 第一天看题自己回答,第二天看牛客网的答案! 1 什么是Java虚拟机?为什么Java被称作是“平台无 ...
- 牛客网《BAT面试算法精品课》学习笔记
目录 牛客网<BAT面试算法精品课>学习笔记 牛客网<BAT面试算法精品课>笔记一:排序 牛客网<BAT面试算法精品课>笔记二:字符串 牛客网<BAT面试算法 ...
- C++版 - HDUoj 2010 3阶的水仙花数 - 牛客网
版权声明: 本文为博主Bravo Yeung(知乎UserName同名)的原创文章,欲转载请先私信获博主允许,转载时请附上网址 http://blog.csdn.net/lzuacm. C++版 - ...
- 牛客网第9场多校E(思维求期望)
链接:https://www.nowcoder.com/acm/contest/147/E 来源:牛客网 题目描述 Niuniu likes to play OSU! We simplify the ...
- 牛客网暑期ACM多校训练营(第七场)Bit Compression
链接:https://www.nowcoder.com/acm/contest/145/C 来源:牛客网 题目描述 A binary string s of length N = 2n is give ...
- Beautiful Numbers(牛客网)
链接:https://ac.nowcoder.com/acm/problem/17385来源:牛客网 题目描述 NIBGNAUK is an odd boy and his taste is stra ...
- 牛客网华为机试题之Python解法
牛客网华为机试题之Python解法 第1题 字符串最后一个单词的长度 a = input().split(" ") print(len(a[-1])) 第2题 计算字符个数 a = ...
- 牛客网Wannafly挑战赛25A 因子(数论 素因子分解)
链接:https://www.nowcoder.com/acm/contest/197/A来源:牛客网 时间限制:C/C++ 1秒,其他语言2秒 空间限制:C/C++ 262144K,其他语言5242 ...
- 牛客网 2018年东北农业大学春季校赛 L题 wyh的天鹅
链接:https://www.nowcoder.com/acm/contest/93/L来源:牛客网 时间限制:C/C++ 3秒,其他语言6秒空间限制:C/C++ 262144K,其他语言524288 ...
随机推荐
- a迭代中的燃尽图统计
简单分析:项目一直在跟进,进展较缓,临近迭代结束,项目进度突飞猛进.
- 转载:如何严格限制session在30分钟后过期!
如何严格限制session在30分钟后过期!1.设置客户端cookie的lifetime为30分钟:2.设置session的最大存活周期也为30分钟:3.为每个session值加入时间戳,然后在程序调 ...
- C#开发BIMFACE系列20 服务端API之获取模型数据5:批量获取构件属性
系列目录 [已更新最新开发文章,点击查看详细] 在<C#开发BIMFACE系列18 服务端API之获取模型数据3:获取构件属性>中介绍了获取单个文件/模型的单个构建的属性,本篇介绍 ...
- Global AI Bootcamp 2019 宁波站活动总结
2019年12月14日,由微软MVP技术社区发起的Global AI Bootcamp 2019盛会在全球60多个国家130个城市点燃.在大中华区,本次活动由全国众多Azure专家及微软MVP技术社区 ...
- 【MySQL报错】ERROR 1290 (HY000): The MySQL server is running with the --secure-file-priv option so it cannot execute this statement
ERROR 1290 (HY000): The MySQL server is running with the --secure-file-priv option so it cannot exec ...
- javascript 模块化 (切记:学习思想)
模块化(切记:学习思想) 如果不用模块化编写代码,那么会具有以下问题: 代码杂乱无章,没有条理性,不便于维护,不便于复用 很多代码重复.逻辑重复 全局变量污染 不方便保护私有数据(闭包) 模块化的基本 ...
- mysql中的ifnull()函数判断空值
我们知道,在不同的数据库引擎中,内置函数的实现.命名都是存在差异的,如果经常切换使用这几个数据库引擎的话,很容易会将这些函数弄混淆. 比如说判断空值的函数,在Oracle中是NVL()函数.NVL2( ...
- Zabbix 预警问题-预警对应的用户报警媒介收不到
问题背景 公司现在有这种需求,需要我们对关键的预警发送到对应的项目组负责人,比如 保险项目组的服务器预警大于警告的预警发送到保险负责人的邮箱(也会发送给运维的,背锅逃不掉的). 进行创建一个 用户群组 ...
- C#上手练习2(FOR语句)
循环语句和条件语句一样都是每个程序中必不可少的,循环语句是用来完成一些重复的工作的,以减少编写代码的工作量. C# for 循环是最常用的循环语句,语法形式非常简单,多用于固定次数的循环. 具体的语法 ...
- 区块链社交APP协议分析:BeeChat
- BeeChat是什么 - BeeChat报文情况 BeeChat使用过程中产生的报文如下: 可以看到,其使用443端口,但内容并非SSL承载,格式不符合SSL,内容中含MsgNtf等明文串,但大部 ...
