Action介绍

在RDD上计算出来一个结果

把结果返回给driver program或保存在文件系统，count(),save

常用的Action



reduce()

接收一个函数，作用在RDD两个类型相同的元素上，返回新元素。

可以实现，RDD中元素的累加，计数，和其它类型的聚集操作。

举例：

val rdd = sc.parallelize(Array(1,2,3,3))

rdd.collect()

collect()

遍历整个RDD，想driver program返回RDD的内容

需要单机内存能容纳下（因为数据要拷贝给driver，一般是测试的时候使用）

大数据的时候，使用saveAsTextFile() action等。

take(n)

返回RDD中的n个元素（同时尝试访问最少的的partitions）

返回结果是无序的，一般为测试时候使用

top(n)

返回排序后的前n个，（根据RDD中的数据比较器）

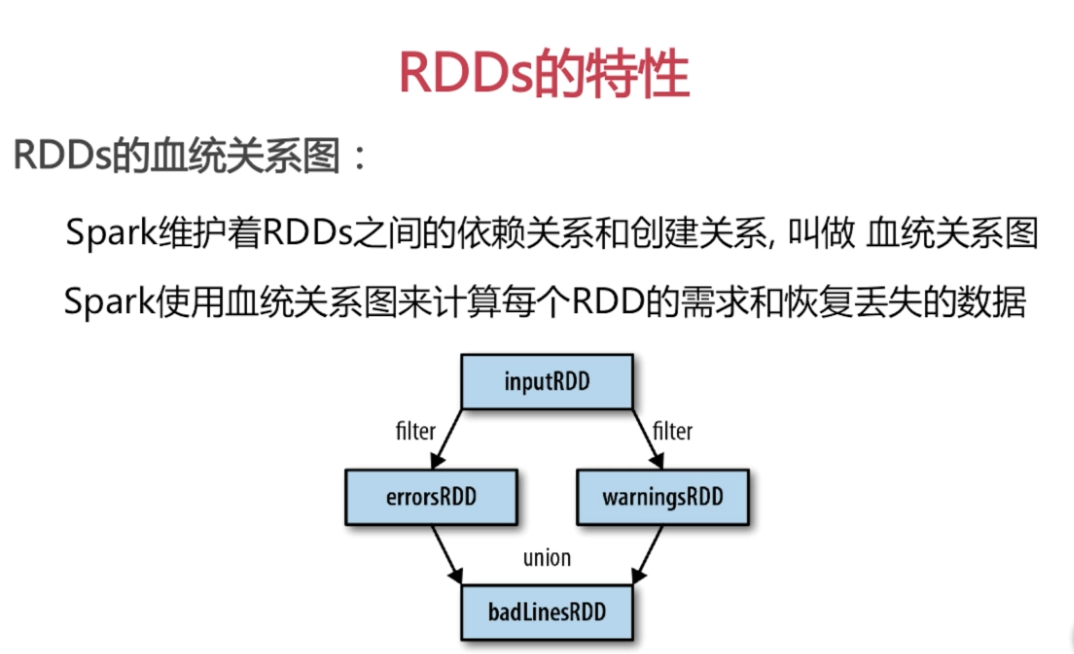
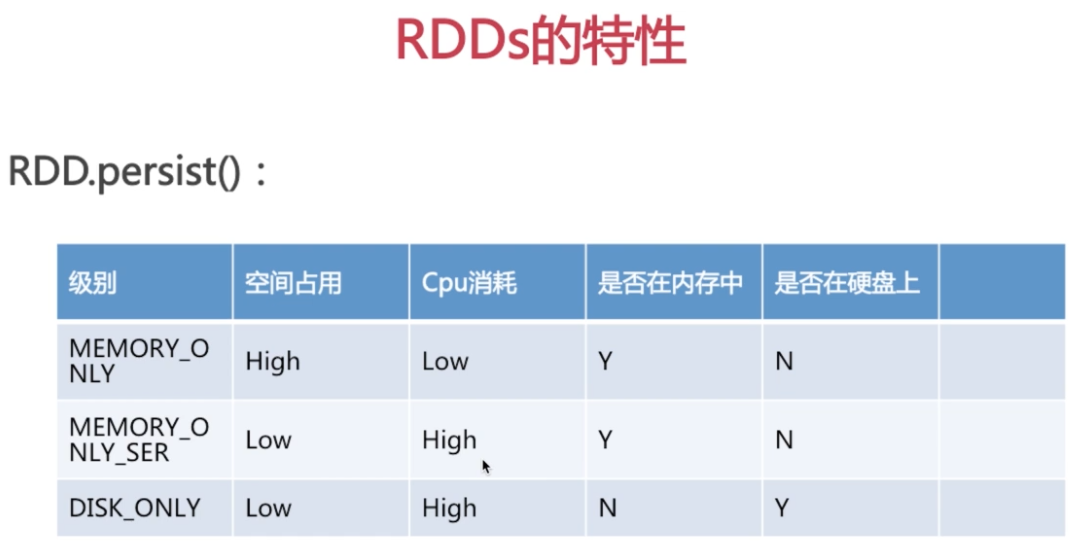
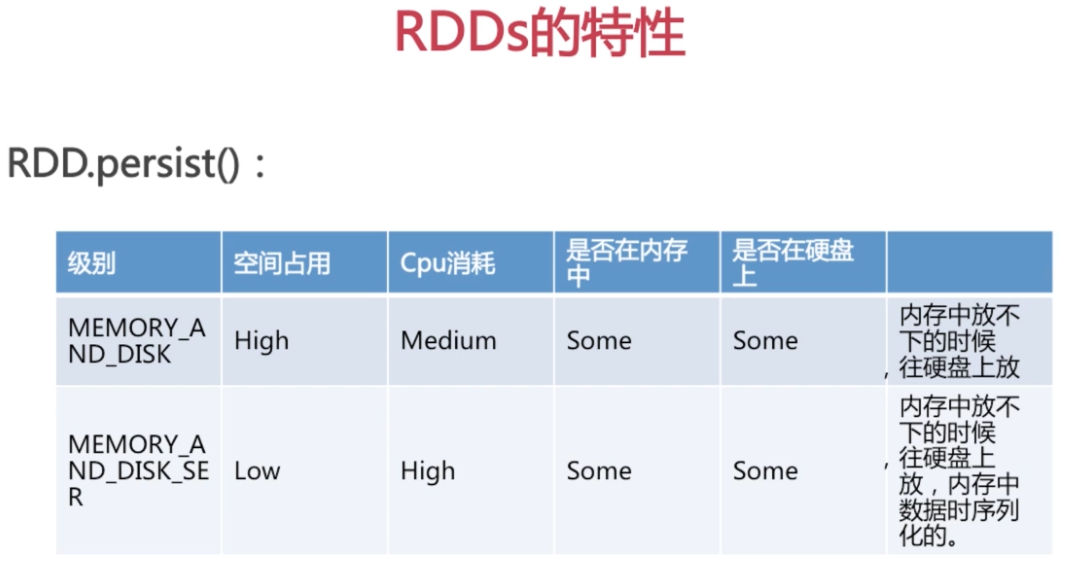
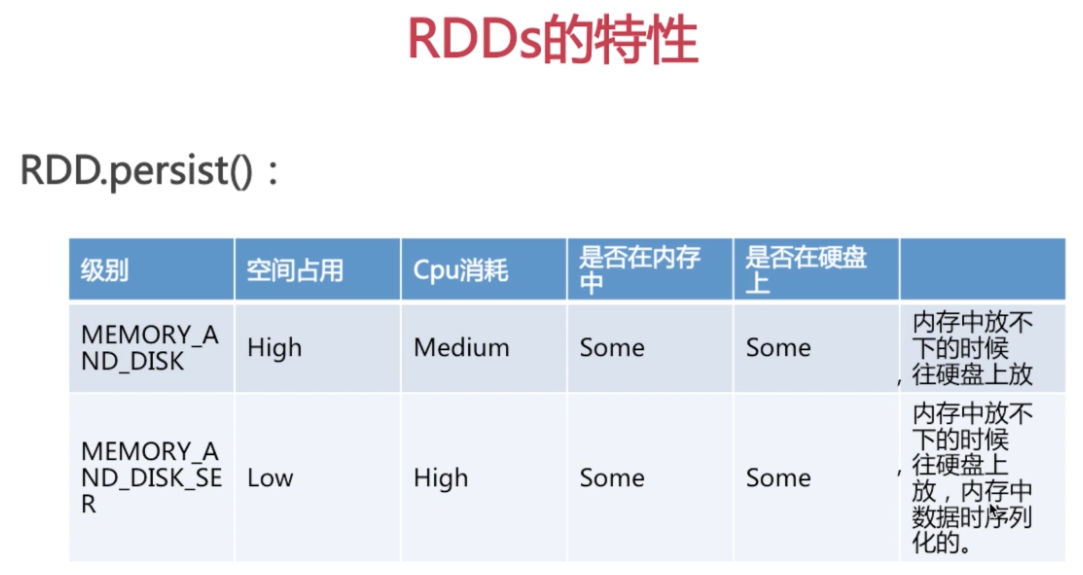
RDD的特性











RDD基本操作之Action的更多相关文章

  1. Spark RDD/Core 编程 API入门系列 之rdd实战（rdd基本操作实战及transformation和action流程图）（源码）（三）

    本博文的主要内容是: 1.rdd基本操作实战 2.transformation和action流程图 3.典型的transformation和action RDD有3种操作: 1.  Trandform ...

  2. spark中RDD的transformation&action

    简介: 1,transformation是得到一个新的RDD,方式很多,比如从数据源生成一个新的RDD,从RDD生成一个新的RDD 2,action是得到一个值,或者一个结果(直接将RDDcache到 ...

  3. Spark笔记：RDD基本操作（上）

    本文主要是讲解spark里RDD的基础操作.RDD是spark特有的数据模型,谈到RDD就会提到什么弹性分布式数据集,什么有向无环图,本文暂时不去展开这些高深概念,在阅读本文时候,大家可以就把RDD当 ...

  4. spark RDD transformation与action函数整理

    1.创建RDD val lines = sc.parallelize(List("pandas","i like pandas")) 2.加载本地文件到RDD ...

  5. spark rdd Transformation和Action 剖析

    1.看到 这篇总结的这么好, 就悄悄的转过来,供学习 wordcount.toDebugString查看RDD的继承链条 所以广义的讲,对任何函数进行某一项操作都可以认为是一个算子,甚至包括求幂次,开 ...

  6. RDD之六：Action算子

    本质上在Actions算子中通过SparkContext执行提交作业的runJob操作,触发了RDD DAG的执行. 根据Action算子的输出空间将Action算子进行分类:无输出. HDFS. S ...

  7. Spark笔记：RDD基本操作（下）

    上一篇里我提到可以把RDD当作一个数组,这样我们在学习spark的API时候很多问题就能很好理解了.上篇文章里的API也都是基于RDD是数组的数据模型而进行操作的. Spark是一个计算框架,是对ma ...

  8. Spark 基础及RDD基本操作

    什么是RDD RDD(Resilient Distributed Dataset)叫做分布式数据集,是Spark中最基本的数据抽象,它代表一个不可变.可分区.里面的元素可并行计算的集合.RDD具有数据 ...

  9. rdd 基本操作

    package com.jason.example import org.apache.spark.rdd.RDD class RddTest extends SparkInstance { val ...

随机推荐

  1. P3195 [HNOI2008]玩具装箱TOY 斜率优化dp

    传送门:https://www.luogu.org/problem/P3195 题目描述 P教授要去看奥运,但是他舍不下他的玩具,于是他决定把所有的玩具运到北京.他使用自己的压缩器进行压缩,其可以将任 ...

  2. Java生产者消费者的三种实现

    Java生产者消费者是最基础的线程同步问题,java岗面试中还是很容易遇到的,之前没写过多线程的代码,面试中被问到很尬啊,面完回来恶补下.在网上查到大概有5种生产者消费者的写法,分别如下. 用sync ...

  3. 随笔编号-11 阿里云CentOS7系列二 -- 安装Tomcat7的方法

    前面讲到了JDK在CentOS7 环境下的安装步骤.这次来分享安装Tomcat7的安装步骤: Tomcat7 安装包: 链接: http://pan.baidu.com/s/1geKwASN 密码: ...

  4. Codeforces 220C

    题意略. 思路: 我们可以把 bi[ i ] 在 ai[ ] 中的位置记录下来,然后算出 i - mp[ bi[i] ] ,再将它压入一个multiset.每次我们就二分地来寻找离0最近的数字来作为答 ...

  5. 2016 ACM-ICPC 青岛站网络赛G题 题解

    [参考博客][https://blog.csdn.net/Tawn0000/article/details/82255682] 题意: 将n个数按照每k个一组来合并,合并需要花费的cost是两个数的长 ...

  6. ZYNQ Block Design中总线位宽的截取与合并操作

    前言 在某些需求下,数据的位宽后级模块可能不需要原始位宽宽度,需要截位,而某些需求下,需要进行多个数据的合并操作. 在verilog下,截位操作可如下所示: wire [7:0] w_in; wire ...

  7. POJ-1511 Invitation Cards( 最短路，spfa )

    题目链接:http://poj.org/problem?id=1511 Description In the age of television, not many people attend the ...

  8. 模板汇总——splay

    #define lch(x) tr[x].son[0] #define rch(x) tr[x].son[1] ; , root; struct Node{ ], pre, sz; void init ...

  9. Codeforces Round #484 (Div. 2) B. Bus of Characters（STL+贪心）982B

    原博主:https://blog.csdn.net/amovement/article/details/80358962 B. Bus of Characters time limit per tes ...

  10. lightoj 1095 - Arrange the Numbers（dp+组合数）

    题目链接:http://www.lightoj.com/volume_showproblem.php?problem=1095 题解:其实是一道简单的组合数只要推导一下错排就行了.在这里就推导一下错排 ...