【算法•日更•第十九期】动态规划：RMQ问题

▎前言

　　首先先来说一下RMB是什么，当然是人民币啦。

　　今天我们要学的这个东西不一般，叫做RMQ问题，那么它和RMB有什么关系呢？待小编细细说来。

▎前置技能：动态规划

　　不会的同志请戳这里迅速了解动态规划。

▎RMQ问题是什么

☞『定义』

　　RMQ (Range Minimum/Maximum Query)问题是指：对于长度为n的数列A，回答若干询问RMQ(A,i,j)(i,j<=n)，返回数列A中下标在i,j里的最小(大）值，也就是说，RMQ问题是指求区间最值的问题。(copy自百度)

　　猜你也不想看，来，小编用人话翻译一下：就是说给定一堆数字（顺序位置固定且永远不变），（多次）询问你一段区间内的最大/最小值。

☞『问题解决：模拟算法』

　　RMQ只是一类这样的问题，却不是一门算法。

　　既然是问题，那么我们就应该解决，但是怎么解决，怎样解决，一切先从模拟算法（直白一点叫暴力）说起。

　　先来想想模拟算法怎么解决，当然是给定区间后直接遍历，寻找最大/最小值呗。但是别忘了，这种题多次询问，一直遍历对于数据规模大的题简直是杯水车薪。

　　此时，不得不请出动态规划。

☞『问题解决：动态规划』

　　我们为什么使用动态规划呢？先来思考这个问题：为什么暴力不能满足需求。

　　你肯定会说：这还不简单，暴力慢呗。

　　但是暴力究竟慢在了哪里？暴力慢在了没有完全利用好整个大区间，很多东西都在重复遍历。

　　那么什么东西能很好的利用大区间呢？我们就会自然的想到了动态规划（感觉属于区间动态规划）。

　　既然多次询问，那么就变向的告诉了我们一定要预处理，这里我们的动态规划可以O(n log n)预处理，然后O(1)查询。

　　先来思考怎么设计状态，最开始小编是这样想的，既然是区间型动态规划类问题，那么就让f[i][j]表示i~j区间内的最大/最小数吧，(以最大数为例)状态转移方程自然就是f[i][j]=max(f[i][k],f[k+1][j])。(k为随机一个i~j区间的数组下标，不过小编更喜欢取中点)

　　后来发现一本通提高篇上的设计状态更好，更快捷，我设计的太慢了。一本通提高篇上是这样处理的：f[i][j]表示i~2^j-1区间内的最大/最小数，那么我们可以仿照之前我的想法，分一半，就是这样的:

　　

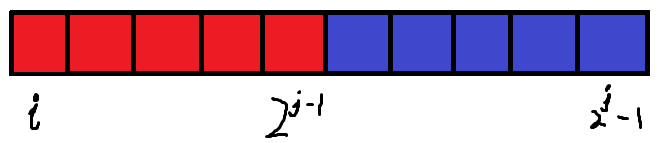
　　从区间初始和结束位置改成动态规划的形式后就是这样的：f[i][j-1]和f[i+2^j-1][j-1]，有时候奇数和偶数是不一样的，所以小编的图可能对这两个式子来说不太标准。

　　那么我们要求的最大最小值就很简单了。

　　但是问题又来了，我们如何面对询问呢？

　　我们可以以二为底，将这个区间内数字的个数次方（幂的逆运算）为界，进行比较两个区间大小，图解一下：

　　

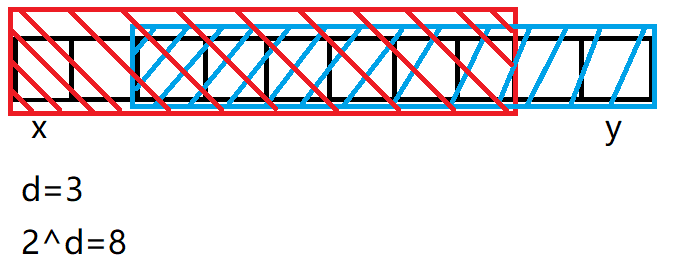
　　那么我们就只要比较出两个区间中的最大最小值即可。两个区间改成动态规划形式就是f[x][log[d]],f[y-(1<<log[d])+1][log[d]])，其中我把d改成了y-x+1的意思。

　　好了，问题又来了，log怎么处理，我们先来看一下前10个数的log处理情况：

　　

　　经过专业调查和探寻后，就会发现log[i]=log[i/2]+1的规律，因此我们可以预处理出log的值。

☞『这么快的算法，为什么还需要其他算法呢？』

　　其实这个问题正是这个算法的弊端，因为不能支持期间修改一些数的值。

　　而线段树，树状数组正巧妙的解决了这一弊端。

▎实战演练：洛谷P1816 忠诚（模板题）

　　废话不多说，直接上题：

---

P1816 忠诚

题目描述

老管家是一个聪明能干的人。他为财主工作了整整10年，财主为了让自已账目更加清楚。要求管家每天记k次账，由于管家聪明能干，因而管家总是让财主十分满意。但是由于一些人的挑拨，财主还是对管家产生了怀疑。于是他决定用一种特别的方法来判断管家的忠诚，他把每次的账目按1，2，3…编号，然后不定时的问管家问题，问题是这样的：在a到b号账中最少的一笔是多少？为了让管家没时间作假他总是一次问多个问题。

输入输出格式

输入格式：

输入中第一行有两个数m,n表示有m(m<=100000)笔账,n表示有n个问题，n<=100000。

第二行为m个数,分别是账目的钱数

后面n行分别是n个问题,每行有2个数字说明开始结束的账目编号。

输出格式：

输出文件中为每个问题的答案。具体查看样例。

输入输出样例

输入样例#1： 复制

10 3
1 2 3 4 5 6 7 8 9 10
2 7
3 9
1 10

输出样例#1： 复制

2 3 1

　　这道题相当好做，就是模板题，所以就不解释了，直接上代码：

 #include<iostream>
 using namespace std;
 int m,n,a[],f[][],x,y,log[];
 int main()
 {
     cin>>m>>n;
     for(int i=;i<=m;i++)
     {
         cin>>a[i];
         f[i][]=a[i];
     }
     for(int j=;j<=;j++)
     for(int i=;i+(<<j)-<=m;i++)
     f[i][j]=min(f[i][j-],f[i+(<<(j-))][j-]);
     log[]=;
     for(int i=;i<=;i++)
     log[i]=log[i/]+;
     for(int i=;i<=n;i++)
     {
         cin>>x>>y;
         int d=y-x+;
         cout<<min(f[x][log[d]],f[y-(<<log[d])+][log[d]])<<" ";
     }
     return ;
 }

▎实战演练：一本通1541：【例 1】数列区间最大值（模板题）

　　废话不多说，直接上题：

---

1541：【例 1】数列区间最大值

时间限制: 1000 ms         内存限制: 524288 KB
提交数: 638     通过数: 224

【题目描述】

输入一串数字，给你 M 个询问，每次询问就给你两个数字 X,Y，要求你说出 X 到 Y 这段区间内的最大数。

【输入】

第一行两个整数 N,M 表示数字的个数和要询问的次数；

接下来一行为 N 个数；

接下来 M 行，每行都有两个整数 X,Y。

【输出】

输出共 M 行，每行输出一个数。

【输入样例】

10 2
3 2 4 5 6 8 1 2 9 7
1 4
3 8

【输出样例】

5
8

【提示】

数据范围与提示：

对于全部数据，1≤N≤10⁵,1≤M≤10⁶,1≤X≤Y≤N。数字不超过 C/C++ 的 int 范围。

【来源】

无

　　这道题只要把忠诚的代码改成max就可以了（还稍微有点其他细节），注意会卡常数，不能用cin和cout。代码如下：

　　

 #include<iostream>
 #include<cstdio>
 using namespace std;
 int m,n,a[],f[][],x,y,log[];
 int main()
 {
     scanf("%d%d",&m,&n);
     for(int i=;i<=m;i++)
     {
         scanf("%d",&a[i]);
         f[i][]=a[i];
     }
     for(int j=;j<=;j++)
     for(int i=;i+(<<j)-<=m;i++)
     f[i][j]=max(f[i][j-],f[i+(<<(j-))][j-]);
     log[]=;
     for(int i=;i<=m;i++)
     log[i]=log[i>>]+;
     for(int i=;i<=n;i++)
     {
         scanf("%d%d",&x,&y);
         int d=y-x+;
         printf("%d \n",max(f[x][log[d]],f[y-(<<log[d])+][log[d]])) ;
     }
     return ;
 }