Rikka with Prefix Sum（组合数学）

Rikka with Prefix Sum

题目描述

Prefix Sum is a useful trick in data structure problems.
For example, given an array A of length n and m queries. Each query gives an interval [l,r] and you need to calculate . How to solve this problem in O(n+m)? We can calculate the prefix sum array B in which B_i is equal to . And for each query, the answer is B_r-B_l-1.
Since Rikka is interested in this powerful trick, she sets a simple task about Prefix Sum for you:
Given two integers n,m, Rikka constructs an array A of length n which is initialized by A_i = 0. And then she makes m operations on it.
There are three types of operations:
1. 1 L R w, for each index i ∈ [L,R], change A_i to A_i + w.
2. 2, change A to its prefix sum array. i.e., let A' be a back-up of A, for each i ∈ [1,n], change A_i to .
3. 3 L R, query for the interval sum .

Intput:

The first line contains a single number t(1≤ t ≤ 3), the number of the testcases.
For each testcase, the first line contains two integers n,m(1 ≤ n,m ≤ 10^5)
And then m lines follow, each line describes an operation(1 ≤ L ≤ R≤ n, 0 ≤ w ≤ 10^9).
The input guarantees that for each testcase, there are at most 500 operations of type 3.

output:

For each query, output a single line with a single integer, the answer modulo 998244353.

test:

Intput:

1
100000 7
1 1 3 1
2
3 2333 6666
2
3 2333 6666
2
3 2333 6666

output

13002
58489497
12043005

中文题意：给定一个序列A，长度最长为100000，初始值为0，现在有三种操作：

1.对区间[l,r]中所有的数都加上一个值。

2.对整个序列求一次前缀和。

3.询问[l,r]区间内所有a的和。

现在对1,0,0,0求3次前缀和得到下图

可以发现(1,1)对右下角的点的贡献是

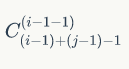
接下来我们定义一个变量now记录数组了进行了几次求数组前缀和也就是题目的2号操作。

对于操作1，在[l,r]区间内每个数增加w。

相当于在上次进行2号操作前，在点 L 增加w，在点 R+1 减少w。

例如：在3到5号位置增加1

序号    1 2 3 4 5 6 7 8 9

now     0 0 1 1 1 0 0 0 0     求前缀和后

now-1  0 0 1 0 0 -1 0 0 0   求前缀和前

对于询问的话只要求下次求完前缀和 （位置 R 的值） - （位置 L-1 的值）

对于进行前缀和操作只要将now++即可

具体操作看代码

 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;
 typedef long long ll;
 const int maxn = ,mod=;
 struct Stack
 {
     ll lie,time,value;
 } st[maxn];
 ll fac[maxn+],ifac[maxn+],top;

 ll quick_pow(ll a,ll b)
 {
     ll ans=;
     while(b)
     {
         if(b&)
             ans=1ll*ans*a%mod;
         a=1ll*a*a%mod;
         b>>=;
     }
     return ans;
 }

 void init()
 {
     fac[]=;
     for(int i=; i<=maxn; i++)
         fac[i]=1ll*fac[i-]*i%mod;
     ifac[maxn]=quick_pow(fac[maxn],mod-);
     for(int i=maxn-; i>=; i--)
         ifac[i]=1ll*ifac[i+]*(i+)%mod;
 }

 ll C(ll n,ll m)
 {
     return 1ll*fac[n]*ifac[m]%mod*ifac[n-m]%mod;
 }

 inline ll solve(ll x,ll now)
 {
     if(x==)return ;

     ll sum = ;
     for(int i=; i<top; i++) ///计算每个更新对点的贡献值
     {

         if(st[i].lie>x)continue;
         ll lie = st[i].lie;
         ll per = st[i].time;
         ll value = st[i].value;

         ll aa = x-lie + now-per -;
         ll bb = now-per -;

         sum = (sum + value*C(aa,bb)%mod)%mod;
     }
     return sum;
 }

 int main()
 {
     init();  ///预处理阶乘和逆元将计算组合数的时间复杂度降为O(1)
     ll t,n,m,op;
     scanf("%lld",&t);
     while(t--)
     {
         scanf("%lld%lld",&n,&m);
         ll now = ,l,r,value;
         top = ;
         while(m--)
         {
             scanf("%lld",&op);
             if(op==)
             {
                 scanf("%lld%lld%lld",&l,&r,&value);
                 st[top].value = value%mod,st[top].time=now-,st[top].lie=l;
                 top++;
                 st[top].value =(mod-value)%mod,st[top].time=now-,st[top].lie=r+;
                 top++;
                 ///将更新存入数组
             }
             else if(op==)
             {
                 now++;
             }
             else
             {
                 scanf("%lld%lld",&l,&r);
                 ll ans = solve(r,now+)-solve(l-,now+);
                 ans = (ans+mod)%mod;
                 printf("%lld\n",ans);
             }
         }
     }
     return ;
 }