[NOI2001]炮兵阵地 题解
题意
我们先来了解一下基本的位运算
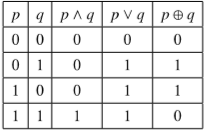
于( \(\bigwedge\) ),或 (\(\bigvee\) ) 异或(\(\bigoplus\))
在下面我们用(&)代表于,(|)代表或
一道状压dp题,状压真的太难了,这道题搞了比较久才弄懂,首先这道题我们是怎么想到状压dp的呢?首先看范围m<=10,数据范围m很小,地图上部分为山地,部分为平原,且放置了的地方左右各两格,上下各两格不能放置,就只存在两种状态,能放与不能放,就可以看为二进制的0 1我们可以对每一行进行状压,但是我们可以发现我们放置第i行时的状态是会影响到第i-1行和第i-2行的,那么我们可以算一下时间复杂度O( 1024^3*100 ) 明显过不去,那么怎么办呢?我们可以仅考虑当前行的合法状态,于前后行无关,故可以先预处理出状态出来,处理出来只有不到70种
我们可以定义状态
f[i][j][k]表示第i行状态为k且上一行状态为j的最大方案数
状态转移方程
dp[i+1][k][l]=max(dp[i+1][k][l],dp[i][j][k]+sum[l]) (sum[l]表示状态为l中1的个数)
1.判断是否为山丘
在输入时将山丘设为1,平原设为0,那么判断状态是否合法就是直接将状态st[i]&dat[1]若为1则说明则说明放在山丘上了
2.判断每个状态有没有两个炮兵左右距离在两格之内
这个可以画个图便可知道当
if(!(i&(i<<1)) && !(i&(i<<2)))
返回值为真时就可以放置,也就是说 i&(i<<1)&&i&(i<<2)返回值为0
3.每一列前两行有没有炮兵 i&j,i&k 若不为0则冲突(j为i前一行,k为j前一行)
代码
#include<bits/stdc++.h>
using namespace std;
const int maxn=110;
int n,m,dp[maxn][maxn][maxn],dat[maxn],sum[maxn],st[maxn],tot,ans;
int clu(int x){
int tmp=0;
while(x){
tmp+=(x&1);
x>>=1;
}
return tmp;
}
int main(){
scanf("%d %d",&n,&m);
for(int i=1;i<=n;++i){
for(int j=0;j<m;++j){
char ch=getchar();
while(ch!='P'&&ch!='H') ch=getchar();
if(ch=='H') dat[i]|=(1<<j);
}
}
for(int i=0;i<(1<<m);++i){
if(!(i&i<<1)&&!(i&i<<2)){
st[++tot]=i;
sum[tot]=clu(i);
}
}
for(int i=1;i<=tot;++i){
if(!(st[i]&dat[1])) dp[1][1][i]=sum[i];
}
for(int i=1;i<n;++i){
for(int j=1;j<=tot;++j){
for(int k=1;k<=tot;++k){
if(!(st[j]&st[k])&&dp[i][j][k]){
for(int l=1;l<=tot;++l){
if(!(st[l]&st[j])&&!(st[l]&st[k])&&!(st[l]&dat[i+1])){
dp[i+1][k][l]=max(dp[i+1][k][l],dp[i][j][k]+sum[l]);
}
}
}
}
}
}
for(int i=1;i<=tot;++i){
for(int j=1;j<=tot;++j){
ans=max(ans,dp[n][i][j]);
}
}
printf("%d",ans);
return 0;
}
[NOI2001]炮兵阵地 题解的更多相关文章
- 洛谷P2704 [NOI2001]炮兵阵地题解
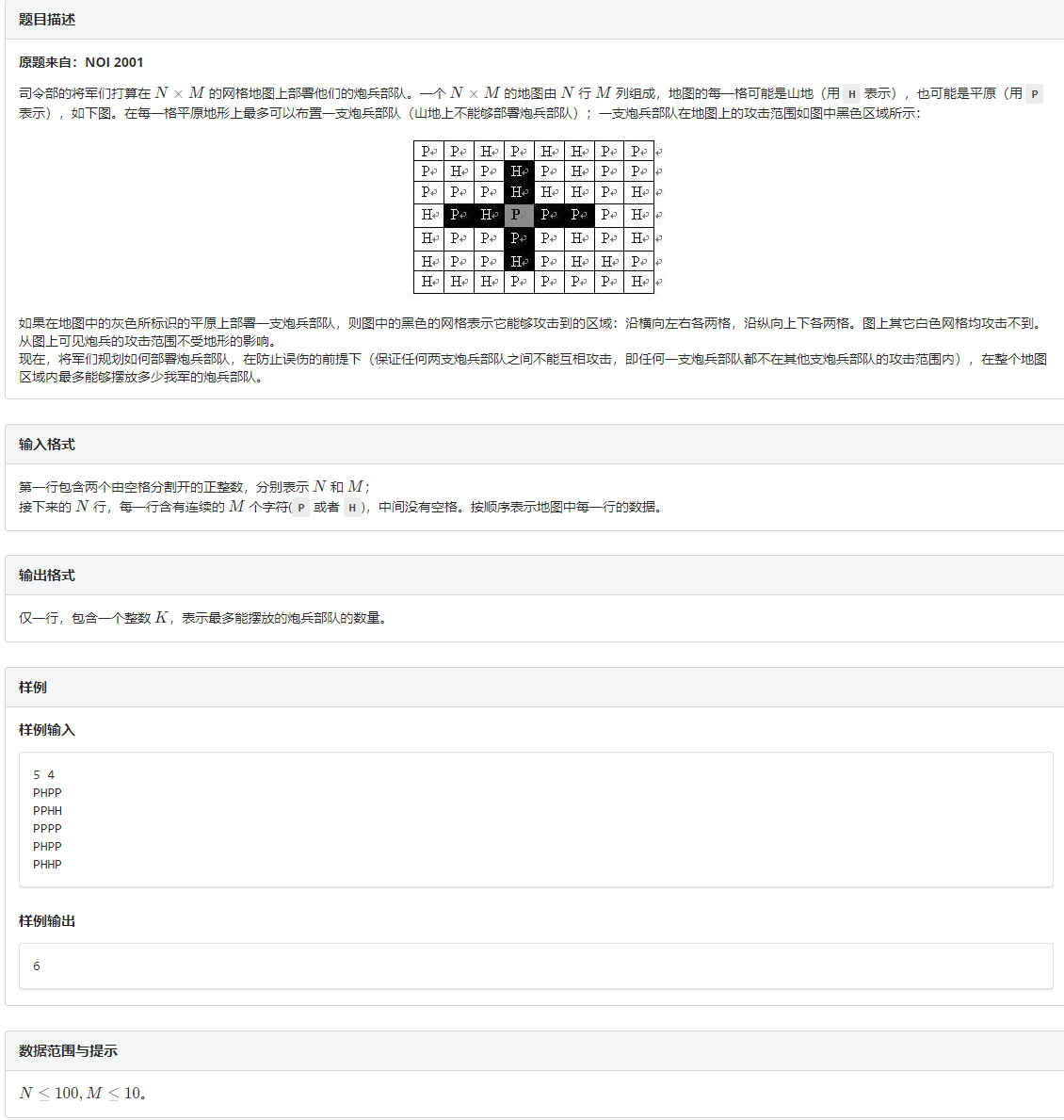
题目描述 司令部的将军们打算在\(N * M\)的网格地图上部署他们的炮兵部队.一个\(N * M\)的地图由N行M列组成,地图的每一格可能是山地(用\("H"\) 表示),也可能 ...
- [洛谷P2704] [NOI2001]炮兵阵地
洛谷题目链接:[NOI2001]炮兵阵地 题目描述 司令部的将军们打算在NM的网格地图上部署他们的炮兵部队.一个NM的地图由N行M列组成,地图的每一格可能是山地(用"H" 表示), ...
- C++ 洛谷 P2704 [NOI2001]炮兵阵地
P2704 [NOI2001]炮兵阵地 没学状压DP的看一下 此题意思很简单,如下图,就是十字架上的不能有两个点放炮兵. 在做此题前,先做一下玉米田 玉米田题解 分析: 而m即一行的个数小于等于10, ...
- P2704 [NOI2001]炮兵阵地 (状压DP)
题目: P2704 [NOI2001]炮兵阵地 解析: 和互不侵犯一样 就是多了一格 用\(f[i][j][k]\)表示第i行,上一行状态为\(j\),上上行状态为\(k\)的最多的可以放的炮兵 发现 ...
- 洛谷P2704 [NOI2001]炮兵阵地 [状压DP]
题目传送门 炮兵阵地 题目描述 司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队.一个N*M的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图 ...
- [Poj1185][Noi2001]炮兵阵地(状压dp)
炮兵阵地 Time Limit: 2000MS Memory Limit: 65536K Total Submissions: 29476 Accepted: 11411 Descriptio ...
- 【题解】洛谷P2704 [NOI2001] 炮兵阵地(状压DP)
洛谷P2704:https://www.luogu.org/problemnew/show/P2704 思路 这道题一开始以为是什么基于状压的高端算法 没想到只是一道加了一行状态判断的状压DP而已 与 ...
- [NOI2001]炮兵阵地 状压DP
题面: 司令部的将军们打算在N*M的网格地图上部署他们的炮兵部队.一个N*M的地图由N行M列组成,地图的每一格可能是山地(用“H” 表示),也可能是平原(用“P”表示),如下图.在每一格平原地形上最多 ...
- 洛谷 P2704 [NOI2001]炮兵阵地
题意简述 给定一张地图,有山地H,平原P,平原可放置炮兵, 炮兵可以攻击沿横向左右各两格,沿纵向上下各两格的区域 求最多放几个炮兵,使他们两两攻击不到 题解思路 枚举第i层,第i - 1层,第i - ...
随机推荐
- JavaScript ES6和ES5闭包的小demo
版权声明:署名,允许他人基于本文进行创作,且必须基于与原先许可协议相同的许可协议分发本文 (Creative Commons) 可能有些小伙伴不知道ES6的写法,这儿先填写一个小例子 let conn ...
- PyCharm如何导入python项目
Pycharm导入python项目 进入PyCharm后,点击File→Open,然后在弹窗中选择需要导入项目的文件夹: 打开了python项目后,需要配置该项目对应的python才可以正常运行: 配 ...
- 解决:Navicat连接不上MySQL 8.0
转载自 https://www.cnblogs.com/shiysin/p/shiysin.html Navicat连接不上,总是报错1251: 原因是MySQL8.0版本的加密方式和MySQL5.0 ...
- 【0728 | 预习】第三篇 Python基础
第三篇 Python基础预习 Part 1 变量 一.什么是变量? 二.为什么要有变量? 三.定义变量 四.变量的组成 五.变量名的命名规范 六.变量名的两种风格 Part 2 常量 Part 3 P ...
- js常见兼容性问题以及解决方法
1.关于使用 event对象,出现的兼容性问题IE/Chrom: event.clientX;event.clientYFF/IE9以上/Chrom: 传参e e.clientX;e.client ...
- javaScript今日总结
javascript简单介绍ECMAScript 1.语法 2.变量:只能使用var定义,如果在函数的内容使用var定义,那么它是一个局部变量,如果没有使用var它是一个全局的.弱类型! 3.数据类型 ...
- Lasso估计论文学习笔记(一)
最近课程作业让阅读了这篇经典的论文,写篇学习笔记. 主要是对论文前半部分Lasso思想的理解,后面实验以及参数估计部分没有怎么写,中间有错误希望能提醒一下,新手原谅一下. 1.整体思路 作者提出了一种 ...
- Kafka之Producer
通过https://www.cnblogs.com/tree1123/p/11243668.html 已经对consumer有了一定的了解.producer比consumer要简单一些. 一.旧版本p ...
- cmd中,查询sqlcmd命令的选项
像我这样的小白,有时候看到-d,-S,-P这些都不知道什么意思,后面知道了是一些命令的选项.如sqlcmd,打开cmd,输入sqlcmd -? 即可获得选项的含义. .
- OSI七层网络模型与TCP/IP四层模型
1.OSI七层结构图: 2.TCP/IP四层结构图: 3.各层对应的协议 4.OSI七层和TCP/IP四层的区别 OSI网络模型和TCP/IP网络模型对应关系: 5.交换机工作在OSI的哪一层 如果有 ...
