机器学习之SVM调参实例

一、任务

这次我们将了解在机器学习中支持向量机的使用方法以及一些参数的调整。支持向量机的基本原理就是将低维不可分问题转换为高维可分问题，在前面的博客具体介绍过了，这里就不再介绍了。

首先导入相关标准库：

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats

import seaborn as sns;sns.set() # 使用seaborn的默认设置

作为一个例子，首先我们随机生成一些数据，考虑分类任务的简单情况，其中两个类别的点是良好分隔的：

# 随机来点数据  make_blobs为聚类产生数据集
from sklearn.datasets.samples_generator import make_blobs

# center：产生数据的中心点，默认值3
X, y = make_blobs(n_samples=50, centers=2, random_state=0, cluster_std=0.60)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

画出的散点图为当前数据的分布情况

　　

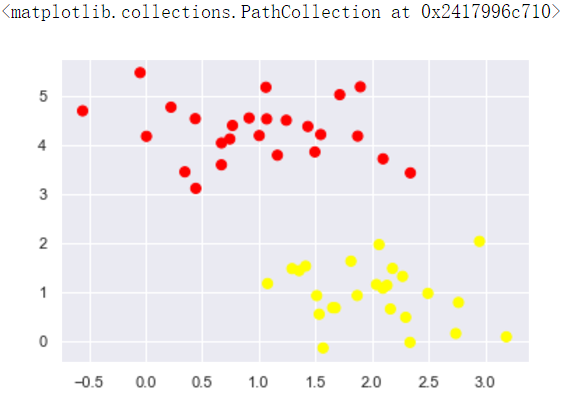
我们将尝试绘制分离两组数据的直线，从而创建分类模型。对于这里所示的二维数据，这是我们可以手动完成的任务。 但是立刻我们看到一个问题：有两个以上的可能的分界线可以完美地区分两个类！

xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plt.plot([0.6], [2.1], 'x', color='red', markeredgewidth=2, markersize=10)

for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
    plt.plot(xfit, m * xfit + b, '-k')

plt.xlim(-1, 3.5)

这些是三个不同的分隔直线，然而，这些分隔直线能够完全区分这些样例。  显然，我们简单的直觉，“在分类之间划线”是不够的，我们需要进一步思考，根据支持向量机的思想，这样划分的效果不太理想。

　　

支持向量机提供了一种改进方法。 直觉是这样的：我们并非在分类之间，简单绘制一个零宽度的直线，而是画出边距为一定宽度的直线，直到最近的点。 这是一个例子：

xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')

for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
    yfit = m * xfit + b
    plt.plot(xfit, yfit, '-k')
    plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
                     color='#AAAAAA', alpha=0.4) # alpha透明度

plt.xlim(-1, 3.5);

如图所示

　　

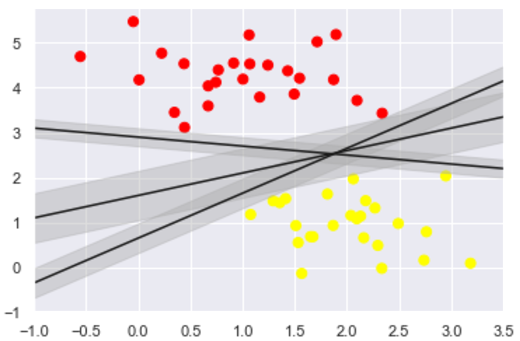
在支持向量机中，边距最大化的直线是我们将选择的最优模型。 支持向量机是这种最大边距估计器的一个例子。

二、训练一个基本的SVM

我们来看看这个数据的实际结果：我们将使用 sklearn 的支持向量分类器，对这些数据训练 SVM 模型。 目前，我们将使用一个线性核并将C参数设置为一个默认的数值。

from sklearn.svm import SVC  # Support Vector Classifier
model = SVC(kernel='linear') # 线性核函数
model.fit(X, y)

得到的SVM模型为

SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
    kernel='linear', max_iter=-1, probability=False, random_state=None,
    shrinking=True, tol=0.001, verbose=False)

为了更好展现这里发生的事情，让我们创建一个辅助函数，为我们绘制 SVM 的决策边界。

#绘图函数
def plot_svc_decision_function(model, ax=None, plot_support=True):
    """Plot the decision function for a 2D SVC"""
    if ax is None:
        ax = plt.gca() # get子图
    xlim = ax.get_xlim()
    ylim = ax.get_ylim()

    # create grid to evaluate model
    x = np.linspace(xlim[0], xlim[1], 30)
    y = np.linspace(ylim[0], ylim[1], 30)
    Y, X = np.meshgrid(y, x) # 生成网格点和坐标矩阵
    xy = np.vstack([X.ravel(), Y.ravel()]).T     # 堆叠数组
    P = model.decision_function(xy).reshape(X.shape)

    # plot decision boundary and margins
    ax.contour(X, Y, P, colors='k',
               levels=[-1, 0, 1], alpha=0.5,
               linestyles=['--', '-', '--']) # 生成等高线 - -

    # plot support vectors
    if plot_support:
        ax.scatter(model.support_vectors_[:, 0],
                   model.support_vectors_[:, 1],
                   s=300, linewidth=1, facecolors='none');
    ax.set_xlim(xlim)
    ax.set_ylim(ylim)

绘出决策边界

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(model);

如图所示：

　　

这是最大化两组点之间的间距的分界线，那中间这条线就是我们最终的决策边界了。 请注意，一些训练点碰到了边缘， 这些点是这种拟合的关键要素，被称为支持向量。 在 Scikit-Learn 中，这些点存储在分类器的support_vectors_属性中：

model.support_vectors_

得到的支持向量的结果

array([[0.44359863, 3.11530945],
       [2.33812285, 3.43116792],
       [2.06156753, 1.96918596]])

在支持向量机只有位于支持向量上面的点才会对决策边界有影响，也就是说不管有多少的点是非支持向量，那对最终的决策边界都不会产生任何影响。我们可以看到这一点，例如，如果我们绘制该数据集的前 60 个点和前120个点获得的模型：

def plot_svm(N=10, ax=None):
    X, y = make_blobs(n_samples=200, centers=2,
                      random_state=0, cluster_std=0.60)
    X = X[:N]
    y = y[:N]
    model = SVC(kernel='linear', C=1E10)
    model.fit(X, y)

    ax = ax or plt.gca()
    ax.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    ax.set_xlim(-1, 4)
    ax.set_ylim(-1, 6)
    plot_svc_decision_function(model, ax)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)
for axi, N in zip(ax, [60, 120]):
    plot_svm(N, axi)
    axi.set_title('N = {0}'.format(N))

观察可以发现分别使用60个和120个数据点，决策边界却没有发生变化。所有只要支持向量没变，其他的数据怎么加无所谓！

　　

三、引入核函数的SVM

首先我们先用线性的核来看一下在下面这样比较难的数据集上还能分了吗？

from sklearn.datasets.samples_generator import make_circles
X, y = make_circles(100, factor=.1, noise=.1) # 二维圆形数据 factor 内外圆比例 (0,1)

clf = SVC(kernel='linear').fit(X, y)

plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf, plot_support=False);

数据集如图所示：

　　

很明显，用线性分类分不了了，那咋办呢？试试高维核变换吧！

#加入了新的维度r
from mpl_toolkits import mplot3d
r = np.exp(-(X ** 2).sum(1))
def plot_3D(elev=30, azim=30, X=X, y=y):
    ax = plt.subplot(projection='3d')
    ax.scatter3D(X[:, 0], X[:, 1], r, c=y, s=50, cmap='autumn')
    ax.view_init(elev=elev, azim=azim) # 设置3D视图的角度  一般都为45
    ax.set_xlabel('x')
    ax.set_ylabel('y')
    ax.set_zlabel('r')

plot_3D(elev=45, azim=45, X=X, y=y)

画出刚才的数据集的一个3维图像

　　

在 Scikit-Learn 中，我们可以通过使用kernel模型超参数，将线性核更改为 RBF（径向基函数，也叫高斯核函数）核来进行核变换，先暂时不管C参数：

#加入径向基函数
clf = SVC(kernel='rbf', C=1E6)
clf.fit(X, y)

得到的SVM模型为

SVC(C=1000000.0, cache_size=200, class_weight=None, coef0=0.0,
    decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
    kernel='rbf', max_iter=-1, probability=False, random_state=None,
    shrinking=True, tol=0.001, verbose=False)

再次进行分类任务

#这回牛逼了！
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
plot_svc_decision_function(clf)
plt.scatter(clf.support_vectors_[:, 0], clf.support_vectors_[:, 1],
            s=300, lw=1, facecolors='none');

分类结果如图

　　

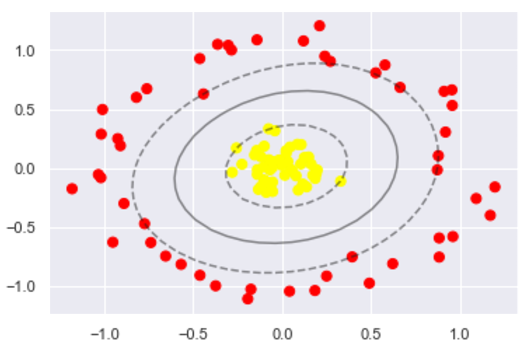
使用这种核支持向量机，我们学习一个合适的非线性决策边界。这种核变换策略在机器学习中经常被使用！

四、软间隔问题

软间隔问题主要是调节C参数， 当C趋近于无穷大时：意味着分类严格不能有错误， 当C趋近于很小的时：意味着可以有更大的错误容忍

X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=0.8)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn');

先看看有噪声点的数据的分布

　　

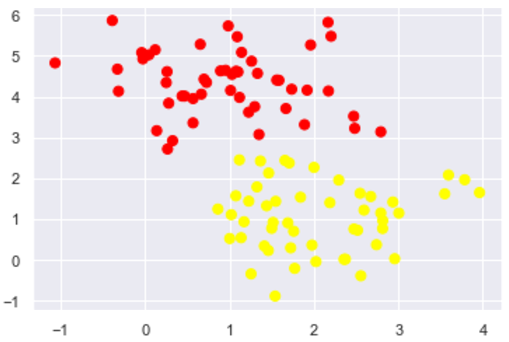
上面的分布看起来要严格地进行划分的话，似乎不太可能，我们可以进行软间隔调整看看

X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=0.8)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

for axi, C in zip(ax, [10.0, 0.1]):
    model = SVC(kernel='linear', C=C).fit(X, y)
    axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_svc_decision_function(model, axi)
    axi.scatter(model.support_vectors_[:, 0],
                model.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none');
    axi.set_title('C = {0:.1f}'.format(C), size=14)

可以比较不同C参数模型地结果，在实际应用中可以适当调整以提高模型的泛化能力。

　　

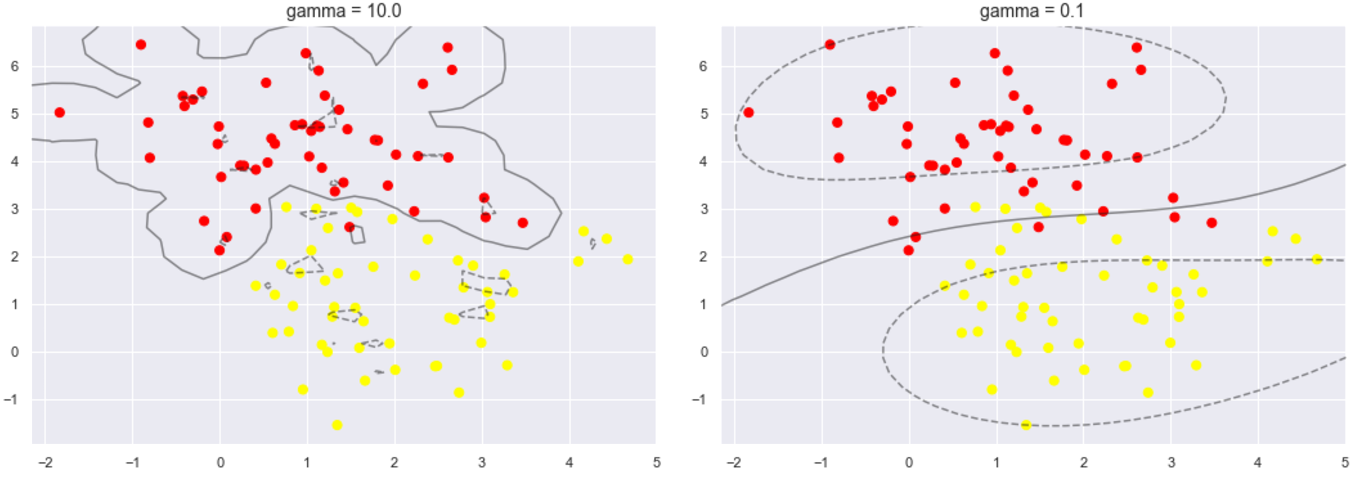
下面再看另一个参数gamma值，这个参数只是在高斯核函数里面才有。这个参数控制着模型的复杂程度，这个值越大，模型越复杂，值越小，模型就越精简。

X, y = make_blobs(n_samples=100, centers=2,
                  random_state=0, cluster_std=1.1)

fig, ax = plt.subplots(1, 2, figsize=(16, 6))
fig.subplots_adjust(left=0.0625, right=0.95, wspace=0.1)

for axi, gamma in zip(ax, [10.0, 0.1]):
    model = SVC(kernel='rbf', gamma=gamma).fit(X, y)
    axi.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='autumn')
    plot_svc_decision_function(model, axi)
    axi.scatter(model.support_vectors_[:, 0],
                model.support_vectors_[:, 1],
                s=300, lw=1, facecolors='none');
    axi.set_title('gamma = {0:.1f}'.format(gamma), size=14)

可以比较一下，当这个参数较大时，可以看出模型分类效果很好，但泛化不太好。当这个参数较小时，可以看出模型里面有些分类是有错误的，但是这个泛化能力更好，一般也应有的更多。

　　

四、总结

通过这次简单的练习，对支持向量机模型有了更加深刻的理解，学习了在支持向量机中SVM的基本使用，以及软间隔参数的调整，还有核函数变化和gamma值等一些参数的比较。