【noip 2011】提高组Day1T3.Mayan游戏

Description

Mayan puzzle是最近流行起来的一个游戏。游戏界面是一个7行5列的棋盘，上面堆放着一些方块，方块不能悬空堆放，即方块必须放在最下面一行，或者放在其他方块之上。游戏通关是指在规定的步数内消除所有的方块，消除方块的规则如下：

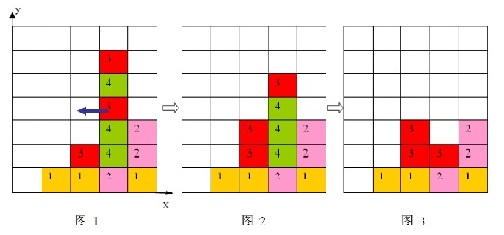
1、每步移动可以且仅可以沿横向（即向左或向右）拖动某一方块一格：当拖动这一方块时，如果拖动后到达的位置（以下称目标位置）也有方块，那么这两个方块将交换位置（参见图6到图7）；如果目标位置上没有方块，那么被拖动的方块将从原来的竖列中抽出，并从目标位置上掉落（直到不悬空，参见图1和图2)；

2、任一时刻，如果在一横行或者竖列上有连续三个或者三个以上相同颜色的方块，则它们将立即被消除（参见图1到图3）。

注意：
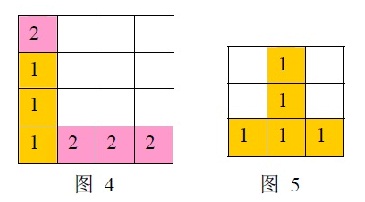
a) 如果同时有多组方块满足消除条件，几组方块会同时被消除（例如下面图4，三个颜色为1的方块和三个颜色为2的方块会同时被消除，最后剩下一个颜色为2的方块）。

b) 当出现行和列都满足消除条件且行列共享某个方块时，行和列上满足消除条件的所有方块会被同时消除（例如下面图5所示的情形，5个方块会同时被消除）。

3、方块消除之后，消除位置之上的方块将掉落，掉落后可能会引起新的方块消除。注意：掉落的过程中将不会有方块的消除。

上面图1到图3给出了在棋盘上移动一块方块之后棋盘的变化。棋盘的左下角方块的坐标为（0, 0），将位于（3, 3）的方块向左移动之后，游戏界面从图1变成图2所示的状态，此时在一竖列上有连续三块颜色为4的方块，满足消除条件，消除连续3块颜色为4的方块后，上方的颜色为3的方块掉落，形成图3所示的局面。

Input

第一行为一个正整数n，表示要求游戏关的步数。

接下来的5行，描述7*5的游戏界面。每行若干个整数，每两个整数之间用一个空格隔开，每行以一个0 结束，自下向上表示每竖列方块的颜色编号（颜色不多于10种，从1开始顺序编号，相同数字表示相同颜色）。

输入数据保证初始棋盘中没有可以消除的方块。

Output

如果有解决方案，输出n行，每行包含3个整数x，y，g，表示一次移动，每两个整数之间用一个空格隔开，其中（x，y）表示要移动的方块的坐标，g表示移动的方向，1表示向右移动，-1表示向左移动。注意：多组解时，按照x为第一关键字，y为第二关键字，1优先于-1，给出一组字典序最小的解。游戏界面左下角的坐标为(0, 0)。

如果没有解决方案，输出一行，包含一个整数-1。

Sample Input

3
1 0
2 1 0
2 3 4 0
3 1 0
2 4 3 4 0

Sample Output

2 1 1
3 1 1
3 0 1

码代码时变量名写错真是一件酸爽的事情TAT

其实比想象中的好写很多，就是烦。

详见代码注释。

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 using namespace std;
 int n,a[][],c[][],sum[];
 struct node{int x,y,dir;}ans[];
 bool empty()//判断是否已经清空
 {
     for(int i=;i<;i++)
         for(int j=;j<;j++)
             if(a[i][j])return false;
     return true;
 }
 void copy(int x[][],int y[][])
 {
     for(int i=;i<;i++)
         for(int j=;j<;j++)
             y[i][j]=x[i][j];
 }
 void drop()//判断掉落
 {
     memset(c,,sizeof(c));
     for(int i=;i<;i++)
         for(int j=,k=;j<;j++)
             if(a[i][j])c[i][k++]=a[i][j];
     copy(c,a);
 }
 bool clear()
 {
     bool flag=false;
     int xx,yy,up,dn;
     for(int i=;i<;i++)//横向判断块数不小于3
         for(int j=;j<;j++)
         if(a[i][j])
         {
             for(xx=i;xx<&&a[xx+][j]==a[i][j];xx++);//横向
             if(xx-i+>=)
             {
                 for(int k=i;k<=xx;k++)
                 {
                     up=j;dn=j;
                     while(up+<&&a[k][up+]==a[k][j])up++;
                     while(dn->=&&a[k][dn-]==a[k][j])dn--;
                     if(up-dn+>=)
                         for(int l=dn;l<=up;l++)
                             a[k][l]=;
                     else a[k][j]=;
                 }
                 flag=true;
             }
         }
     for(int i=;i<;i++)
         for(int j=;j<;j++)//纵向判断块数不小于3
         if(a[i][j])
         {
             for(yy=j;yy+<&&a[i][yy+]==a[i][j];yy++);//纵向
             if(yy-j+>=)
             {
                 for(int k=j;k<=yy;k++)
                 {
                     up=i;dn=i;
                     while(up+<&&a[up+][k]==a[i][k])up++;
                     while(dn->=&&a[dn-][k]==a[i][k])dn--;
                     if(up-dn+>=)
                         for(int l=dn;l<=up;l++)
                             a[l][k]=;
                     else a[i][k]=;
                 }
                 flag=true;
             }
         }
     return flag;
 }
 void dfs(int step)
 {
     if(step>n)//达到步数
     {
         if(empty())
         {
             for(int i=;i<=n;i++)
                 if(ans[i].dir)printf("%d %d -1\n",ans[i].x+,ans[i].y);
                 else printf("%d %d 1\n",ans[i].x,ans[i].y);
             exit();
         }
         return;
     }
     memset(sum,,sizeof(sum));
     for(int i=;i<;i++)
         for(int j=;j<;j++)
             sum[a[i][j]]++;
     for(int i=;i<=;i++)//若当前状态里同种颜色方块数量不足3，直接返回
         if(sum[i]>&&sum[i]<)return;
     for(int i=;i<;i++)//右移优先于左移
         for(int j=;j<;j++)
             if(a[i][j]!=a[i+][j])//若颜色相同则没有移动的必要
             {
                 int b[][];
                 copy(a,b);
                 ans[step]=(node){i,j,!a[i][j]};//注意判断当前方块是否为空
                 swap(a[i][j],a[i+][j]);
                 drop();
                 while(clear())drop();
                 dfs(step+);
                 copy(b,a);
             }
 }
 int main()
 {
     scanf("%d",&n);
     for(int i=;i<;i++)
         for(int j=;;j++)
         {
             scanf("%d",&a[i][j]);
             if(!a[i][j])break;
         }
     dfs();
     printf("-1\n");
     return ;
 }