B树

每个节点都存储key和data，所有节点组成这棵树，并且叶子节点指针为null。

B+树

只有叶子节点存储data，叶子节点包含了这棵树的所有键值，叶子节点不存储指针。

后来，在B+树上增加了顺序访问指针，也就是每个叶子节点增加一个指向相邻叶子节点的指针，这样一棵树成了数据库系统实现索引的首选数据结构。

原因有很多，最主要的是这棵树矮胖，呵呵。一般来说，索引很大，往往以索引文件的形式存储的磁盘上，索引查找时产生磁盘I/O消耗，相对于内存存取，I/O存取的消耗要高几个数量级，所以评价一个数据结构作为索引的优劣最重要的指标就是在查找过程中磁盘I/O操作次数的时间复杂度。树高度越小，I/O次数越少。

那为什么是B+树而不是B树呢，因为它内节点不存储data，这样一个节点就可以存储更多的key。

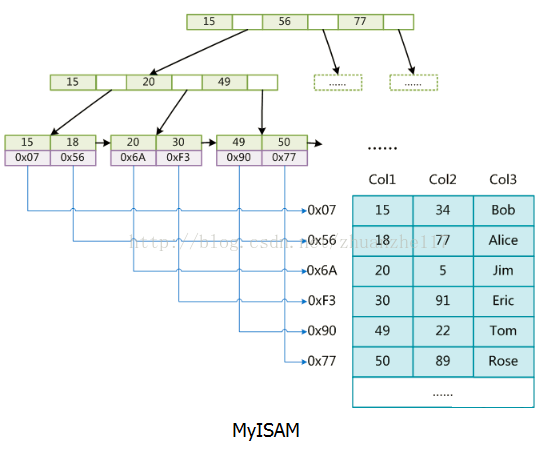
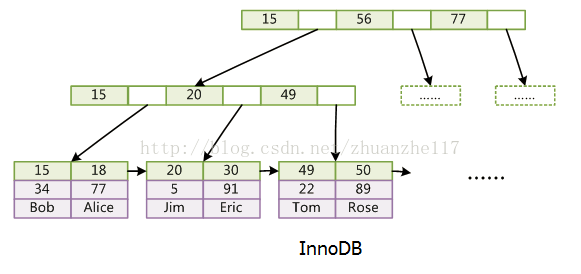
在MySQL中，最常用的两个存储引擎是MyISAM和InnoDB，它们对索引的实现方式是不同的。

MyISAM 

data存的是数据地址。索引是索引，数据是数据。

InnoDB

data存的是数据本身。索引也是数据。

B+树及数据库索引的应用的更多相关文章

  1. B树在数据库索引中的应用剖析

    引言 关于数据库索引,google一个oracle index,mysql index总 有大量的结果,其中很多的使用方法推荐,**索引之n条经典建议云云.笔者认为,较之借鉴,在搞清楚了自己的需求的基 ...

  2. 为什么选择B+树作为数据库索引结构？

    背景 首先,来谈谈B树.为什么要使用B树?我们需要明白以下两个事实: [事实1] 不同容量的存储器,访问速度差异悬殊.以磁盘和内存为例,访问磁盘的时间大概是ms级的,访问内存的时间大概是ns级的.有个 ...

  3. 程序员的算法课（16）-B+树在数据库索引中的作用

    版权声明:本文为博主原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明. 本文链接:https://blog.csdn.net/m0_37609579/article/de ...

  4. B+树作为数据库索引有什么优势？I/O方面？

    首先要了解磁盘预读机制,大致就是说,从磁盘读取数据的速度比从内存读取数据的速度要慢很多,所以要尽量减少磁盘I/O的操作,尽量增加内存I/O操作,既然这样,我们可以从磁盘提前把需要的数据拿到内存,这样需 ...

  5. 【转】B-树和B+树的应用：数据搜索和数据库索引

    B-树 1 .B-树定义 B-树是一种平衡的多路查找树,它在文件系统中很有用. 定义:一棵m 阶的B-树,或者为空树,或为满足下列特性的m 叉树: ⑴树中每个结点至多有m 棵子树: ⑵若根结点不是叶子 ...

  6. 数据结构 B-树和B+树的应用：数据搜索和数据库索引

    B-树 1 .B-树定义 B-树是一种平衡的多路查找树,它在文件系统中很有用. 定义:一棵m 阶的B-树,或者为空树,或为满足下列特性的m 叉树:⑴树中每个结点至多有m 棵子树:⑵若根结点不是叶子结点 ...

  7. B-树和B+树的应用：数据搜索和数据库索引

    B-树和B+树的应用:数据搜索和数据库索引  B-树 1 .B-树定义 B-树是一种平衡的多路查找树,它在文件系统中很有用. 定义:一棵m 阶的B-树,或者为空树,或为满足下列特性的m 叉树:⑴树中每 ...

  8. (转)B-树和B+树的应用：数据搜索和数据库索引

    B-树 1 .B-树定义 B-树是一种平衡的多路查找树,它在文件系统中很有用. 定义:一棵m 阶的B-树,或者为空树,或为满足下列特性的m 叉树: ⑴树中每个结点至多有m 棵子树: ⑵若根结点不是叶子 ...

  9. 为什么MySQL数据库索引选择使用B+树？

    在进一步分析为什么MySQL数据库索引选择使用B+树之前,我相信很多小伙伴对数据结构中的树还是有些许模糊的,因此我们由浅入深一步步探讨树的演进过程,在一步步引出B树以及为什么MySQL数据库索引选择使 ...

随机推荐

  1. Centos使用虚拟环境创建python django工程

    本地环境 通常我们登录就是后就是本地环境 本地环境下查看pip安装了那些包 pip3 list 可以看到本地环境下我们安装的是django1.11.16版本,现在我有个项目要使用django 2.0以 ...

  2. POJ3261-Milk Patterns-后缀数组

    可重叠重复k次的最长子串长度. 还是使用二分答案对heigh数组分组的做法. #include <cstdio> #include <algorithm> #include & ...

  3. Android Dialog 简单封装

    转载:https://www.cnblogs.com/zjjne/archive/2013/10/03/3350382.html public class MyAlertDialog { //regi ...

  4. centos 7创建ss服务（方式一）

    一:安装PIP,由于安装的是python 版本的ss,所以需要先安装PIP: $ curl "https://bootstrap.pypa.io/get-pip.py" -o &q ...

  5. 洛谷P1063能量项链题解

    $题目$ 不得不说,最近我特别爱刷这种区间DP题,因为这个跟其他的DP有些不一样的地方,主要是有一定的套路,就是通过小区间的状态更新大区间,从而得到原题给定区间的最优解. $但是$ 这个题应该跟$石子 ...

  6. Android大学课件SQLite3 数据库操作

    一.数据库介绍 SQLite3:当有大量相似结构的数据需要存储的时候 . 其实SQLite3 就是一个文件,类似之前学过的MySQL SqlServer等. 二.SQLiteOpenHelper 是一 ...

  7. 「中国剩余定理CRT」学习笔记

    设正整数$m_1, m_2, ... , m_r$两两互素,对于同余方程组 $x ≡ a_1 \ (mod \ m_1)$ $x ≡ a_2 \ (mod \ m_2)$ $...$ $x ≡ a_r ...

  8. Error fetching command 'collectstatic': You're using the staticfiles app without having set the STATIC_ROOT setting to a filesystem path. Command 'collectstatic' skipped

    报错现象 报错解决 在 settings.py 中添加这一句话则可以解决 STATIC_ROOT = os.path.join(BASE_DIR, 'static') 测试不在有问题

  9. 【转】MSVCRTD.lib(crtexew.obj) : error LNK2019: 无法解析的外部符号 _WinMain@16，该符号在函数 ___tmainC

    @2018-12-18 [小记] vs-2013 编译 cJSON code in git-hub 时遇见问题 error LNK2019,解决如下 [问题描述]MSVCRTD.lib(crtexew ...

  10. attr prop jquery关于获取DOM属性值的两个函数

    $('#domid').attr('acitve') $('#domid').prop('checked') // 在使用JQUERY获取DOM元素的属性时,有两个函数,attr 和 prop < ...