AlphaGo的前世今生（二）AlphaGo: Countdown to AI Revolution

这是本专题的第二节，在这一节我们将以David Silver等人的Natrue论文Mastering the game of Go with deep neural networks and tree search为基础讲讲AlphaGo的基本框架，力求简洁清晰，具体的算法细节参见原论文。本人水平有限，如有错误还望指正。如需转载，须征得本人同意。

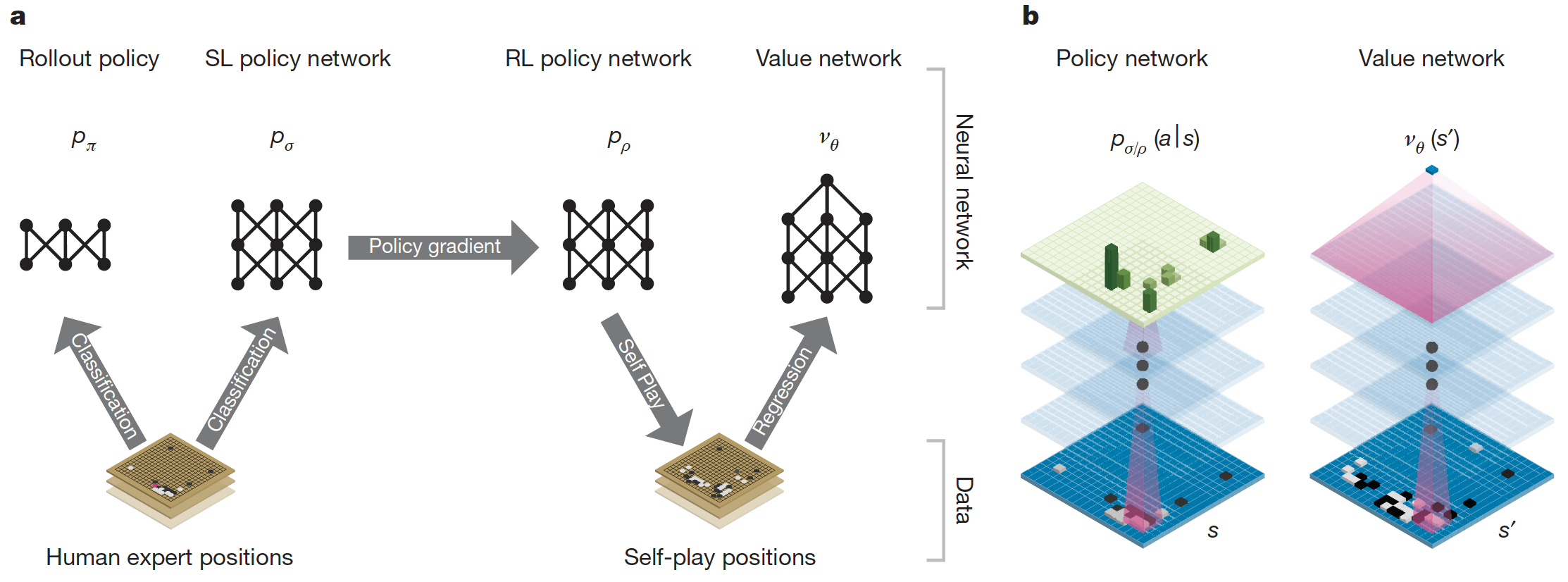
AlphaGo流程

以人类的棋局用监督学习训练出一个策略网络 \(p_\sigma\)
以人类的棋局用监督学习训练出一个策略网络 \(p_\pi\)，此为Rollout策略
以策略网络 \(p_\sigma\)作为初始化，用强化学习训练出策略网络 \(p_\rho\)
以策略网络 \(p_\rho\) 进行自我对局，生成大量棋局样本
以生成的棋局样本用监督学习训练出一个价值网络 \(v_\theta\)
基于策略网络 \(p_\sigma\) 和价值网络 \(v_\theta\)，利用蒙特卡洛树搜索进行动作选取

1. 监督学习策略网络 \(p_\sigma\)

模型：13层卷积神经网络分类模型，最后一层为softmax

数据：16万局大师级人类玩家的棋局，总共有2900万的位置数据，每个位置包含了当前棋局的大致描述和人类所做的动作 \((s, a)\)

输入：19x19x48的三维向量，其中棋盘里的每一个点都被一个48维的特征向量所表示

输出：361个概率值 \(p_\sigma(a|s)\)，对应了棋盘上的每个位置

训练：50块GPU训练了3亿4千万步，历时3周，在验证集上准确率为57%

用途：用于作为强化学习训练的初始值，以及蒙特卡洛搜索树的先验概率。

2. 监督学习Rollout策略网络 \(p_\pi\)

模型：简单的线性softmax网络

数据：800万步人类棋局动作

输入：局部特征，比监督学习策略网络的特征能更快地通过计算得到

输出：361个概率值 \(p_\pi(a|s)\)，对应了棋盘上的每个位置

训练：验证集上准确率为24.2%

备注：此策略网络选择动作只需2微秒，对比监督学习策略网络需要3毫秒；此策略网络在每个线程每秒平均能模拟1000局棋局

3. 强化学习策略网络 \(p_\rho\)

模型：和监督学习策略网络类似的结构，权重初始化为 \(\rho = \sigma\)

方法：使用蒙特卡洛策略梯度REINFORCE（带有基线值）算法对监督学习得到的策略进行提升

环境：对手是策略池里随机选出来的策略（策略池由先前经过不同循环次数的策略网络构成）

状态：和监督学习策略网络的特征相同

动作：下棋的位置

奖励：当前策略网络获胜得到+1，反之-1

训练：自我对战了128万局之后实战对阵监督学习策略网络，根据训练出的升级版 softmax 策略进行动作采样，胜率为80%

用途：自我对局生成棋局数据，供监督学习价值网络进行训练

4. 强化学习自我对局

动机：利用数据集里的棋局进行监督学习训练出的价值网络带有严重的过拟合，究其原因，是因为原始棋局里连续几步的相关性很强，只差一个子但回归目标值都是一样的。

解法：利用策略网络 \(p_\rho\) 进行自我对局，生成3000万个不同的位置数据，这些数据是从互不相同的同等数量棋局里采样得到。

过程：

随机生成一个数字 \(U\sim unif\{1, 450\}\)
以监督学习策略网络 \(p_\sigma\) 生成前 \(U-1\) 步棋
从可选的动作里随机取一个，\(a_U\sim unif\{1, 361\}\)
从第 \(U+1\) 步开始以强化学习策略网络 \(p_\rho\) 生成余下棋局直至结束，获取奖励 \(z_t\)
将 \((s_{U+1}, z_{U+1})\) 加入数据集

注意前三步是为了增加数据集的多样性。

5. 监督学习价值网络 \(v_\theta\)

模型：和监督学习策略网络类似的结果，只是最后一层为单值输出

数据：强化学习自我对局产生的3000万个 \((s_t, z_t)\) 数据

输入：和监督学习策略网络的特征相同，多了一个当前哪个颜色走子的特征

输出：当前状态的值函数 \(v_\theta(s)\)

训练：50块GPU训练了一周

用途：蒙特卡洛搜索树中估计叶结点的值函数

6. 蒙特卡洛树搜索

论文中采用的是全新的蒙特卡洛搜索树算法，被称为APV-MCTS，Asynchronous Policy and Value MCTS algorithm。

蒙特卡洛搜索树总共分成四步执行：

选择。从根节点开始基于UCB1算法进行动作选择，直到到达叶结点。

\[
a_t = \arg\max (Q(s_t, a) + u(s_t, a)) \\
u(s, a) \varpropto \frac{P(s, a)}{1+N(s, a)}
\]

一开始算法会倾向于高先验概率低访问次数的动作，但之后算法会倾向于选择动作值较大的动作。

扩展。访问次数超过某个阙值时，则将后续的状态 \(s' = f(s, a)\) 加入到搜索树中，先验概率 \(P(s, a)\) 设为监督学习策略网络输出的概率值 \(p_\sigma(a|s')\)
评估。用监督学习价值网络对叶结点进行值估计得到 \(v_\theta(s_L)\)，用Rollout策略走到棋局终点，得到奖励 \(z_t\)
更新。叶结点的值函数是 \(v_\theta(s_L)\) 和 \(z_L\) 的加权和。

\[
V(s_L) = (1-\lambda)v_\theta(s_L) + \lambda z_L \\
N(s, a) = \sum\limits_{i=1}^n1(s, a, i) \\
Q(s, a) = \frac{1}{N(s, a)}\sum\limits_{i=1}^{n}1(s, a, i)V(s_L^i)
\]

\(s_L^i\) 指第\(i\)次模拟的叶结点, \(1(s, a, i)\) 指 \((s, a)\) 在第\(i\)次模拟中是否被访问。

搜索完成后，算法会选择访问次数最多的根结点动作作为最终做出的动作。

备注

生成对抗网络（GAN）：在某种意义上，AlphaGo 的自我对局训练已经有了对抗，每次迭代都试图找到上一代版本的“反策略”。
DeepMind 和 Facebook 研究这个问题大概是在同一时间，是什么让AlphaGo这么拿到了围棋最高段位？
Facebook更专注于监督学习，这是当时最厉害的项目之一。我们选择更多地关注强化学习，是因为相信它最终会超越人类的知识。最近的研究结果显示，只用监督学习的方法的表现力惊人，但强化学习绝对是超出人类水平的关键。

参考文献：
[1] Mastering the game of Go with deep neural networks and tree search. David Silver et al. 2016. https://www.nature.com/articles/nature16961
[2] Reinforcement learning: An introduction 2nd Edition. Richard Sutton. 2018. http://www.incompleteideas.net/book/bookdraft2017nov5.pdf
[3] UCL course on Reinforcement Learning. David Silver. 2015. http://www0.cs.ucl.ac.uk/staff/d.silver/web/Teaching.html
[4] Ask me Everything on Reddit. David Silver and Julian Schrittwieser. http://www.sohu.com/a/199027080_610300