Improving Deep Neural Networks: Hyperparameter tuning, Regularization and Optimization（第一周）深度学习的实践层面 (Practical aspects of Deep Learning)

1. Setting up your Machine Learning Application

1.1 训练，验证，测试集(Train / Dev / Test sets)

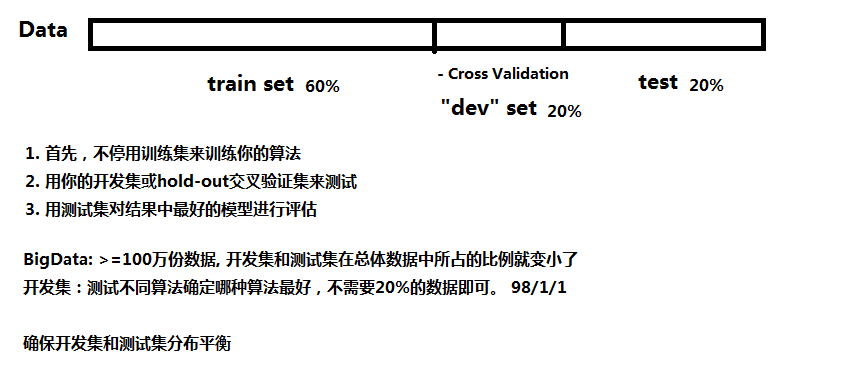
1.2 Bias/Variance(偏差和方差)

• 高偏差(high bias)称为"欠拟合"(underfitting), 练集误差与验证集误差都高.
• 高方差(high variance)称为过拟合(overfitting), 训练集误差很低而验证集误差很高.

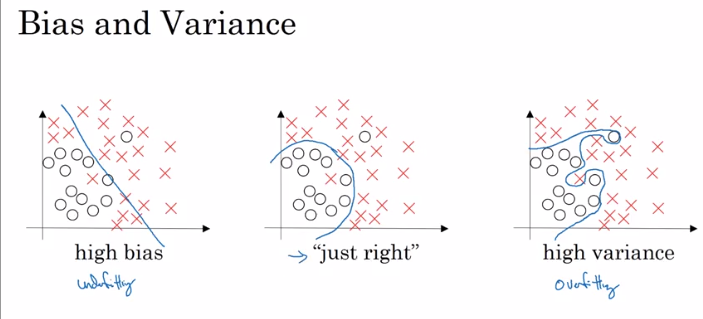
1.3 Basic "recipe" for Machine learning

1.31 High bias(高偏差)

• 更大的神经网络

1.32 High Variance(高方差)

• 更多数据
• 正则化
• CNN

2. Regularizing your neural network(发生过拟合—高方差)

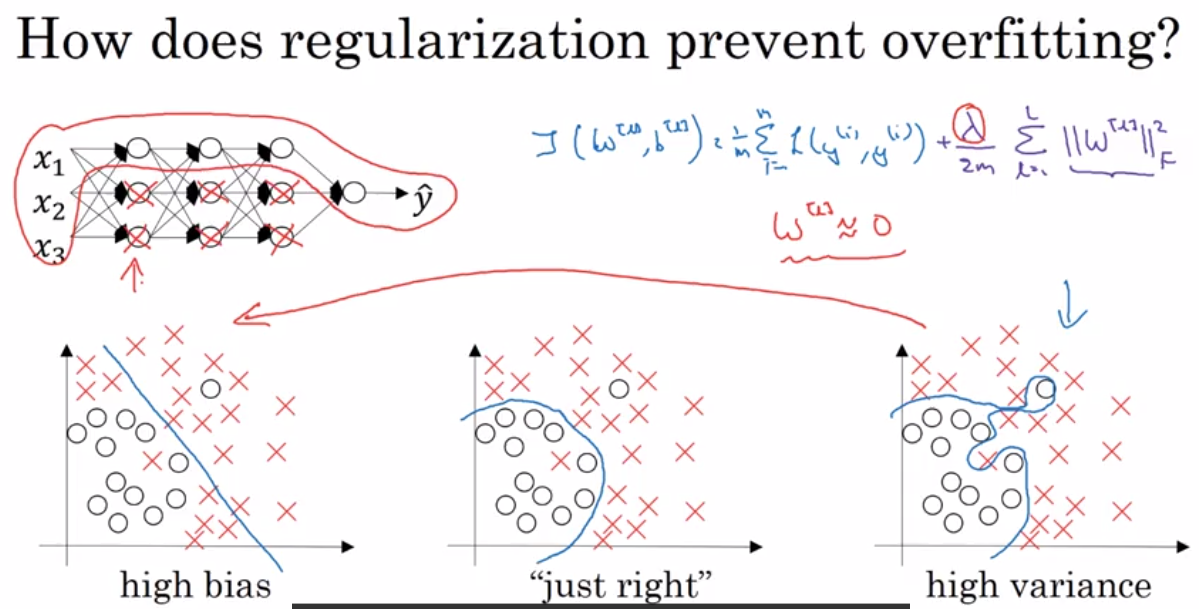
2.1 L2正则化(权重衰减)

正则项说明，无论$w^[l]$是什么，我们都试图使之更小(趋于0)。则计算得的 $z[l]=w[l]a[l−1]+b[l]$ 更容易(以tanh例)落在激活函数 $g(z[l])$ 中间那一段接近线性的部分, 以达到简化网络的目的(线性的激活函数使得无论多少层的网络, 效果都和一层一样)。

注意：J(..)代价函数，需要加上 $\frac{\lambda}{m}w^{[l]}$

2.2 随机失活(Dropout)正则化

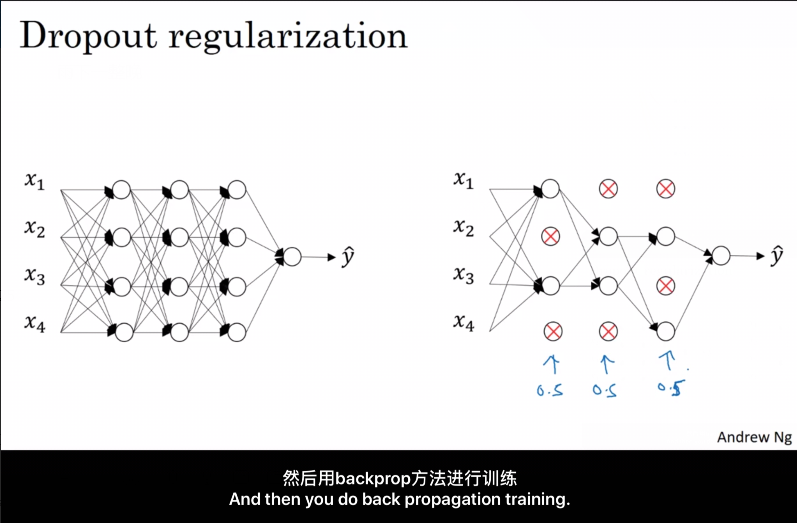
对每一轮的训练, Dropout 遍历网络的每一层, 设置神经网络中每一层每个节点的失活概率, 不参与本轮的训练, 于是得到一个更小的网络.

最常用的为 反向随机失活(Inverted Dropout).

该方法在向前传播时, 根据 随机失活的概率 (例如0.2), 将每一层(例如 $l$层)的 $a^{[l]}$ 矩阵($a=g(z)$)中被选中失活的元素置为0，则该层的 $a^{[l]}$ 相当于少了 20% 的元素. 为了不影响下一层 $ z^{[l+1]} $ 的期望值, 我们需要 $a^{[l]}$ /= 0.8 以修正权重.

由于训练时的 "$a^{[l]}$ /= 0.8" 修复了权重, 在测试阶段无需使用 Dropout。

注：Dropout 不能与梯度检验同时使用, 因为 Dropout 在梯度下降上的代价函数J难以计算.

3. 归一化(Normalizing)

训练神经网络，其中一个加速训练的方法就是归一化输入。假设一个训练集有两个特征，
输入特征为 2 维，归一化需要两个步骤：(一些特征0~1，一些0~1000)

1. 零均值化：

   1. μ $ =\frac{1}{m}\sum^m_{i=1}x^{(i)} $；

   2. $ x:=x-μ $
      

1. 归一化方差：

   1. ρ $ ^2=\frac{1}{m}\sum^m_{i=1}x^{(i)}**2 $

   2. x /= ρ^2

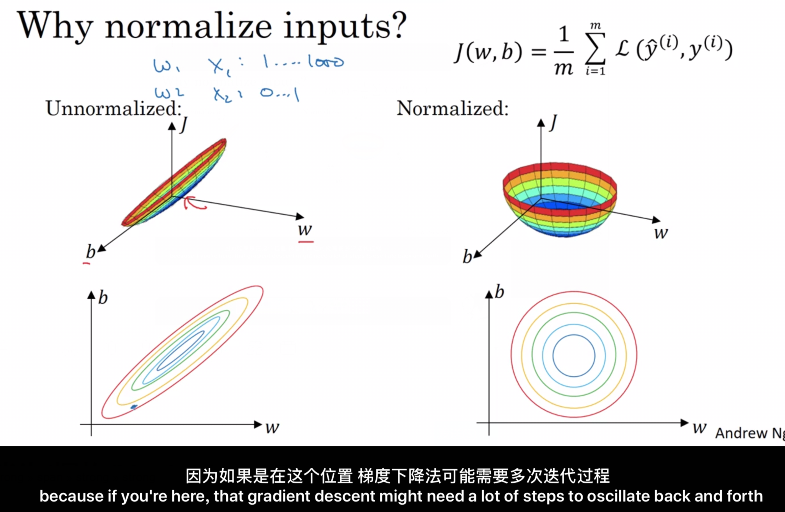
归一化直观的理解就是使得代价函数更圆, 更容易优化代价函数.

4. 梯度消失/爆炸(Vanishing / Exploding Gradients

为了方便理解，假设使用了线性激活函数 g(z)=z , 且：

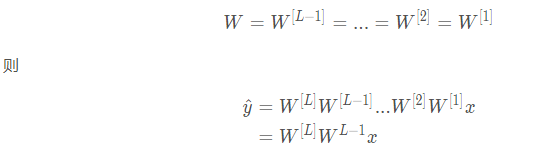
可知若 $W$ 中有元素权重为 1.5 , 则最终得到 $1.5^{L-1}$ , 若层数很深, 计算得 $yˆ \hat{y}$ 也很大; 同理，若权重为 0.5 , 进行 $L−1$次幂运算后值会很小. 这便是梯度爆炸与梯度消失.

有效的解决方案：由于 $z=w1x1+w2x2+...+wnxn$ (忽略 b), 为了预防 $z$太大或太小, 则$n$ 越大时, 期望 $w_i$ 越小, 则在随机(0~1)初始化$W$ 时, 我们对其乘上一个小于1的倍数, 使之更小。

• 对于Tanh, 权重乘上 $\sqrt{\frac{1}{n^{[l-1]}}} $, 或者 $ \sqrt{\frac{2}{n^{[l-1]}+n^{[l]}}}$

• 对于Relu, 权重乘上 $\sqrt{\frac{2}{n^{[l-1]}}} $

5. 梯度检验

在反向传播的时候, 如果怕自己 $d\theta[i] = \frac{\partial J}{\partial \theta_i}$ 等算错, 可以用导数的定义, 计算：

$d\theta_{approx}[i] = \frac{J(\theta_1, \theta_2,..., \theta_i + \varepsilon, ...) - J(\theta_1, \theta_2, ..., \theta_i - \varepsilon, ...)}{2\varepsilon}$

然后根据两者误差估计自己是否算错. 该方法仅用来调试, 且不能同 Dropout 同时使用.