day53-马踏棋盘
马踏棋盘
1.算法优化的意义
- 算法是程序的灵魂,为什么有些程序可以在海量数据计算时,依旧保持高速计算?
- 编程中算法很多,比如八大排序算法(冒泡、选择、插入、快排、归并、希尔、基数、堆排序)、查找算法、分治算法、动态规划算法、KMP算法、贪心算法、普利姆算法、克鲁斯卡尔算法、迪杰斯特拉算法、弗洛伊德算法
- 下面以骑士周游问题为例,体验算法优化程序的意义,感受算法的威力
2.骑士周游问题
- 马踏棋盘算法介绍和游戏演示
- 马踏棋盘算法也被称为骑士周游问题
- 将马随机放在国际象棋的8*8棋盘Board[0-7][0-7]的某个方格中,马按走棋规则移动(马只能走日字)。要求每个方格只进入一次,走遍棋盘上全部64个方格
- 会使用到图的遍历算法(DFS)+贪心算法优化
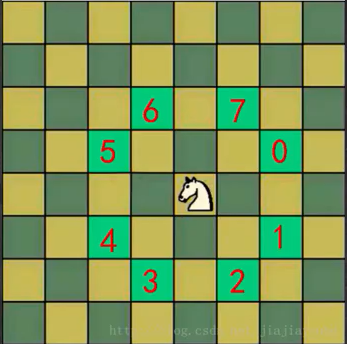
马踏棋盘(骑士周游问题)实际上是图的深度优先搜索(DFS)的应用。
使用回溯(就是深度优先搜索)来解决,假如马儿踏了53个点,如图,走到了第53个,坐标为(1,0),发现已经走到了尽头,没办法,那就只能回退了,查看其它的路径,就在棋盘上不停地回溯……
这里我们先用基本的方法解决,然后使用贪心算法(greedyalgorithm)进行优化。解决马踏棋盘问题,体会到不同的算法对程序效率的影响
3.思路分析
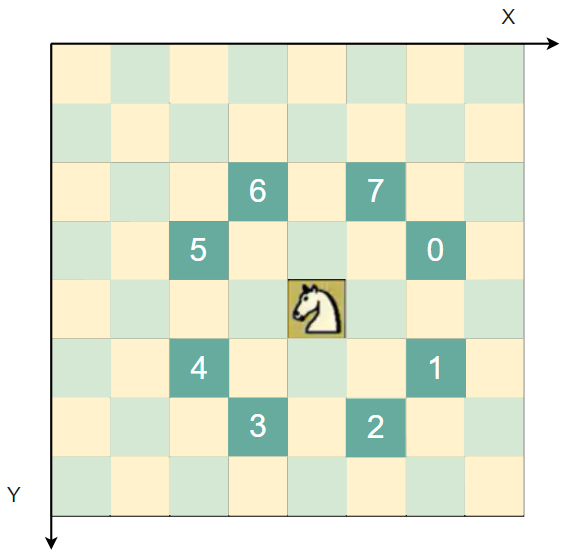
- 创建一个棋盘chessBoard,是一个二维数组
- 将马儿当前位置设置为已经访问,然后根据当前位置,计算马儿还能走哪些位置,并放入到一个集合中(ArrayList),每一个位置的下一步最多有8个方向,每走一步,就使用step+1
- 遍历ArrayList中存放的所有位置,看看哪个可以走,如果可以走通,就继续,走不通,就回溯
- 判断马儿是否完成了任务,使用step和应该走的步数比较,如果没有达到数量,则表示没有完成任务,将整个棋盘设置为0
注意:马儿走的策略不同,得到的结果也会不一样,效率也不一样。
package li;
import java.awt.*;
import java.util.ArrayList;
/**
* @author 李
* @version 1.0
* 马踏棋盘
*/
public class HorseChessBoard {
//定义属性
private static int X = 6;//表示col-列
private static int Y = 6;//表示row-行
private static int[][] chessBoard = new int[Y][X];//棋盘
private static boolean[] visited = new boolean[X * Y];//表示记录某个位置是否走过
private static boolean finished = false;//记录马儿是否遍历完棋盘
public static void main(String[] args) {
//测试
int row = 2;
int col = 2;
long start = System.currentTimeMillis();
traversalChessBoard(chessBoard, row-1, col-1, 1);//将棋盘上开始的位置设置为起始第一步
long end = System.currentTimeMillis();
System.out.println("遍历耗时="+(end - start));
//输出当前棋盘的情况
for (int[] rows : chessBoard) {
for (int step : rows) {//step表示 这个位置是马儿应该走的第几步
System.out.print(step + "\t");
}
System.out.println();
}
}
//最核心的算法,遍历棋盘,如果遍历成功,就将finished的值设置为true,
//并且将马儿走的每一步step记录到chessBoard
public static void traversalChessBoard(int[][] chessBoard, int row, int col, int step) {
//先将step记录到chessBoard
chessBoard[row][col] = step;
//把这个位置设置为已经访问
visited[row * X + col] = true;//就是将二维数组的下标对应到一位数组下标,按行的顺序存放(注意下标从0开始)
//获取当前位置可以走的下一个位置有哪些
ArrayList<Point> ps = next(new Point(col, row));//注意col-X,row-Y
//遍历
while (!ps.isEmpty()) {
//取出当前ps集合的第一个位置(点)
Point p = ps.remove(0);//每取出一个点,就从集合中删除这个点
//判断该点的位置是否走过,如果没有走过,就递归遍历
if (!visited[p.y * X + p.x]) {
//递归遍历
traversalChessBoard(chessBoard, p.y, p.x, step + 1);
}
}
//当退出while循环后,看看是否遍历成功,如果没有成功,就重置相应的值,然后进行回溯
if (step < X * Y && !finished) {
//重置
chessBoard[row][col] = 0;
visited[row * X + col] = false;
} else {
finished = true;
}
}
//编写方法,可以获取当前位置 可以走的下一步 的所有位置(Point表示x,y)
public static ArrayList<Point> next(Point curPoint) {//curPoint表示当前点
//先创建一个ArrayList
ArrayList<Point> ps = new ArrayList<>();
//创建一个Point对象,表示一个位置/点,准备放入到 ps集合中
Point p1 = new Point();
//判断在curPoint位置,是否可以走如下位置,如果可以走,就将该点(p1)放入到集合ps中
/**
* 马走日的话,每个点就有八个方向可以走,并且这八个方向对于当前坐标的相对坐标都是固定的,
* 通过当前坐标算出八个方向的相对坐标,然后排除掉那些可能会走出界的方向
*/
//判断是否可以走5位置
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y - 1) >= 0) {
ps.add(new Point(p1));//要创建一个新的点
}
//判断是否可以走6位置
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y - 2) >= 0) {
ps.add(new Point(p1));//要创建一个新的点
}
//判断是否可以走7位置
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y - 2) >= 0) {//注意索引的范围是:0到X-1
ps.add(new Point(p1));//要创建一个新的点
}
//判断是否可以走0位置
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y - 1) >= 0) {
ps.add(new Point(p1));//要创建一个新的点
}
//判断是否可以走1位置
if ((p1.x = curPoint.x + 2) < X && (p1.y = curPoint.y + 1) < Y) {
ps.add(new Point(p1));//要创建一个新的点
}
//判断是否可以走2位置
if ((p1.x = curPoint.x + 1) < X && (p1.y = curPoint.y + 2) < Y) {
ps.add(new Point(p1));//要创建一个新的点
}
//判断是否可以走3位置
if ((p1.x = curPoint.x - 1) >= 0 && (p1.y = curPoint.y + 2) < Y) {
ps.add(new Point(p1));//要创建一个新的点
}
//判断是否可以走4位置
if ((p1.x = curPoint.x - 2) >= 0 && (p1.y = curPoint.y + 1) < Y) {
ps.add(new Point(p1));//要创建一个新的点
}
return ps;
}
}
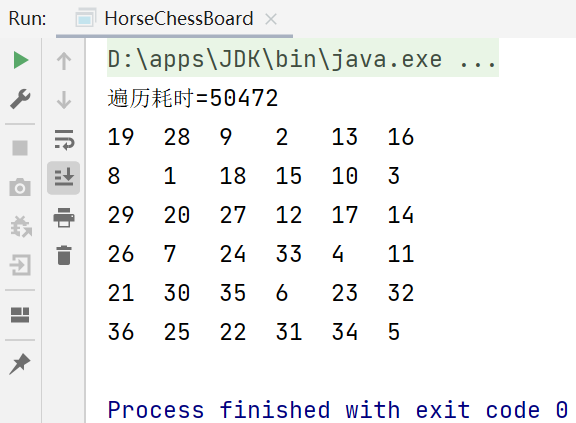
4.优化

- 根据上面的代码,当前点走的下一个位置,是按照我们的顺时针方向来挑选位置的,因此,所选择的点的下一个可以走的位置的个数是不确定的
- 优化的思路是:我们应该优先选择的下一个位置,这个位置的再下一个位置应该尽可能少,这样就可以减少回溯的次数
- 代码:对ps集合按照可以走的下一个位置的次数进行升序排序(从小到大排序)
修改:
- 编写方法
//写一个方法,对ps集合的各个位置,可以走的下一个位置的次数进行排序,把可能走的下一个位置从小到大进行排序
public static void sort(ArrayList<Point> ps){
ps.sort(new Comparator<Point>() {
@Override
public int compare(Point o1, Point o2) {
return next(o1).size()-next(o2).size();
}
});
}
- 在递归中调用该方法,对ps集合按照可以走的下一个位置的次数进行升序排序(从小到大排序)
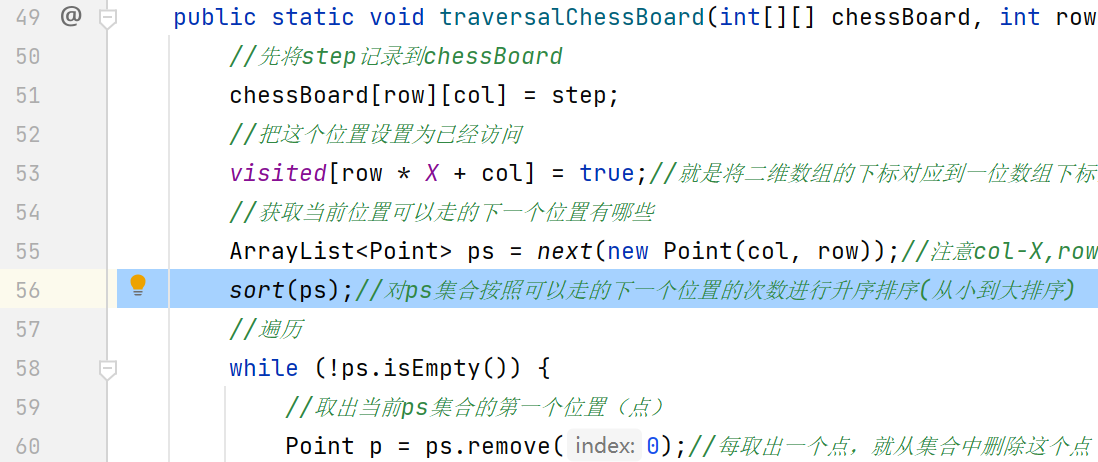
优化结果:
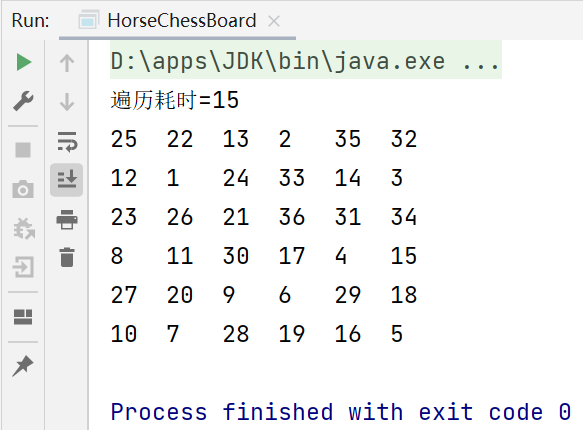
day53-马踏棋盘的更多相关文章
- 马踏棋盘问题-贪心(MATLAB&C++)
原创文章,转载请注明:马踏棋盘问题-贪心(MATLAB&C++) By Lucio.Yang 1.问题描述 将马随机放在国际象棋的Board[0-7][0-7]的某个方格中,马按走棋规则进行移 ...
- 剑指Offer_12_矩阵中的路径(参考问题:马踏棋盘)
题目描述 请设计一个函数,用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径.路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向左,向右,向上,向下移动一个格子.如果一条路径经过了矩阵 ...
- java实现马踏棋盘问题
1.问题描述: 在国际象棋中,马走日,用户输入棋盘的起始位置从x:0-4,y:0-3输出从这一点开始,马走完整个棋盘的各个方案,并输出方案数 2.输入样式: 请输入棋盘马起始位置: 0 0 3.输出样 ...
- C++代码审查---审查孙晓宁马踏棋盘谜题程序
与孙晓宁同学结对审查,其代码地址如下:https://github.com/brunnhilder/-1/blob/master/%E9%A9%AC%E8%B8%8F%E6%A3%8B%E7%9B%9 ...
- python 回溯法 子集树模板 系列 —— 18、马踏棋盘
问题 将马放到国际象棋的8*8棋盘board上的某个方格中,马按走棋规则进行移动,走遍棋盘上的64个方格,要求每个方格进入且只进入一次,找出一种可行的方案. 分析 说明:这个图是5*5的棋盘. 图片来 ...
- 马踏棋盘--dfs
[问题描述]关于马踏棋盘的基本过程:国际象棋的棋盘为 8*8 的方格棋盘.现将"马"放在任意指定的方格中,按照"马"走棋的规则将"马"进行移 ...
- 马踏棋盘算法递归+回溯法实现 C语言
r为矩阵的行,c为矩阵的列 将结果输出到当前目录下的results.txt. 结果将给出:1.是否存在路径使马可以按要求走遍所有的方格: 2.解的总数: 3.程序执行的时间: #include< ...
- F: Horse Pro 马走棋盘 BFS
F: Horse Pro 豆豆也已经开始学着玩象棋了,现在豆豆已经搞清楚马的走法了,但是豆豆不能确定能否在 100 步以内从一个点到达另一个点(假设棋盘无限大). Input 第一行输入两个整数 x1 ...
- 【面试题】TB
动态库与静态库区别: 堆栈区别,这样区分的意义: 不用第三个变量,交换两个变量的值: 链表公共节点: 判断链表是否有环: 常用排序算法,哪个可以链表实现: 哪科学的好,感兴趣: 项目介绍,遇到的最大问 ...
随机推荐
- DOM及DOM相关操作
DOM 概述: DOM 全称(document object model)文档对象模型(文档指定为对应html文档),对应的DOM就是操作HTML文档的(增删改查) DOM结构 document 文档 ...
- java数组---特点,边界
数组的四个基本特点 1.其长度是确定的.数组一旦被创建,它的大小就是不可以改变的. 2.其元素必须是相同类型,不允许出现混合类型. 3.数组中的元素可以是任何数据类型,包括基本类型和引用类型. 4.数 ...
- Think PHP框架基础安装6.0
第一步:点击基础安装tp框架composer create-project topthink/think tp 第二步:点击架构多应用模式 拓展composer require topthink/th ...
- 如何使用Postman快速简单的调用快递物流平台快递鸟API接口
前沿 快递鸟是一家聚合类的第三方快递物流平台,目前该平台提供的产品主要以API为主.由于API不能直观的看到产品效果,需要进行API对接联调成功后才能真实的看到产品的实际效果.但是如果一上来就写代码进 ...
- KingbaseES R6 手工创建主备流复制案例
数据库版本: TEST=# select version(); version ---------------------------------------------------------- ...
- KingbaseES 数据库删除功能组件
关键字: KingbaseES.卸载.删除功能 一.安装后检查 在安装完成后,可以通过以下几种方式进行安装正确性验证: 1. 查看安装日志,确认没有错误记录; 2. 查看开始菜单: 查看应用程 ...
- Base64加密、解密
#region Base64加密方法 /// <summary> /// Base64加密,采用utf8编码方式加密 /// </summary> /// <param ...
- C++ "链链"不忘@必有回响之单链表
1. 前言 数组和链表是数据结构的基石,是逻辑上可描述.物理结构真实存在的具体数据结构.其它的数据结构往往在此基础上赋予不同的数据操作语义,如栈先进后出,队列先进先出-- 数组中的所有数据存储在一片连 ...
- MyBatis标签之Select resultType和resultMap
摘要:介绍MyBatis 中Select标签的两个属性resultType和resultMap及其区别. 1 MyBatis动态SQL之if 语句 2 MyBatis动态sql之where标签|转 3 ...
- 将java的项目jar包打成镜像
一.镜像.容器相关知识的概述 Docker 镜像 docker镜像是一个特殊的文件系统,除了提供容器运行时所需的程序.库.资源.配置等文件外,还包含了一些为运行时准备的一些配置参数(如匿名卷.环境变量 ...
