Autobus 方法记录
[COCI2021-2022#4] Autobus
题目描述
在一个国家里有 \(n\) 座城市。这些城市由 \(m\) 条公交线路连接，其中第 \(i\) 条线路从城市 \(a_i\) 出发，到 \(b_i\) 停止，路程中耗时 \(t_i\) 分钟。
Ema 喜欢旅行，但她并不喜欢在公交线路之间换乘。在旅行过程中，她希望最多只需坐 \(k\) 个不同的公交线路。
Ema 想知道，从城市 \(c_i\) 到城市 \(d_i\) 的最短旅行时间是多少（最多坐 \(k\) 个不同的公交线路）。
输入格式
第一行包含两个整数 \(n,m\)，分别表示城市的数量和公交车线路的数量。
接下来 \(m\) 行，第 \(i+1\) 包含三个整数 \(a_i,b_i,t_i\)，分别表示第 \(i\) 条公交车线路的起点、终点和从起点到终点所需的时间。
接下来一行包含两个整数 \(k,q\)，最大坐的不同公交线路的个数和问题题的个数。
接下来 \(q\) 行，第 \(m+j+3\) 行包含两个整数 \(c_j,d_j\)，表示询问从城市 \(c_j\) 到城市 \(d_j\) 的最短旅行时间。
输出格式
输出包含 \(q\) 行，第 \(i\) 行包含一个整数，表示从城市 \(c_i\) 到城市 \(d_i\) 的最短旅行时间。
样例 #1
样例输入 #1
4 7
1 2 1
1 4 10
2 3 1
2 4 5
3 2 2
3 4 1
4 3 2
1 3
1 4
4 2
3 3
样例输出 #1
10
-1
0
样例 #2
样例输入 #2
4 7
1 2 1
1 4 10
2 3 1
2 4 5
3 2 2
3 4 1
4 3 2
2 3
1 4
4 2
3 3
样例输出 #2
6
4
0
样例 #3
样例输入 #3
4 7
1 2 1
1 4 10
2 3 1
2 4 5
3 2 2
3 4 1
4 3 2
3 3
1 4
4 2
3 3
样例输出 #3
3
4
0
提示
【样例解释】
每个样例中的答案都已经标记在图中。
【数据规模与约定】
本题采用子任务捆绑测试。
- Subtask 1（15 pts）：\(k ≤ n ≤ 7\)。
- Subtask 2（15 pts）：\(k ≤ 3\)。
- Subtask 3（25 pts）：\(k ≤ n\)。
- Subtask 4（15 pts）：没有额外限制。
对于 \(100\%\) 的数据，\(2\le n \le 70,1\le m,t_i\le 10^6,1\le a_i,b_i,c_j,d_j\le n,1\le k\le10^9,1\le q \le n^2\)。
【提示与说明】
本题分值按 COCI 原题设置，满分 \(70\)。
题目译自 COCI2021-2022 CONTEST #4 T2 Autobus。
题解
题目的要求是求全源最短路，而且\(n\)（图上总点数）非常小，和\(floyd\)的相性很好，所以首先考虑\(floyd\)算法。
本题的第一个难点在于“最多只需坐\(k\)个不同的公交线路”。但仔细观察数据范围，\(2\le n \le 70,1\le k \le10^9\)，可以见得在大部分情况下，\(k\)是比\(n\)大的。因为每个点至多到一次，所以一个点到该定点的线路也最多走一次，最复杂的旅行方案也只需要走\((n-1)\)条线路。而\(k\)比\(n\)大就意味着旅行不再受“最多只需坐\(k\)个不同的公交线路”的限制。
所以，对于这部分的数据，我们可以跑一个裸的\(floyed\)来处理出图上任意两个点之间的最短路。
if(k>=n)
{
for(int l=1;l<=n;l++)//l枚举断点
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)//floyd标志性的三层for循环
{
ans[i][j]=minn(ans[i][j],ans[i][l]+ans[l][j]);
//ans[i][j]根据floyd算法的定义，为i到j的最短路
}
}
}
}
那么剩下的问题就是处理会受\(k\)值限制的情况了。
既然有一个对经过路径条数限制的条件，那么我们不妨给记录最短路的数组再增加一个维度。
令\(dis[i][j][k]\)表示经过\(k\)条边的前提下，\(i\)到\(j\)的最短路。
再加入\(k\)限制之前，我们先来看看传统的\(floyd\)是如何工作的。
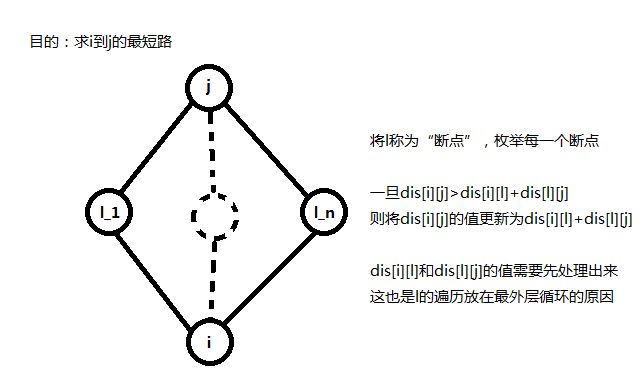
可以直观地看到，类似动态规划，\(dis[i][j]\)可能由\(dis[i][l]+dis[l][j]\)更新而来，或者由\(dis[i][j]\)直接继承。
那么考虑在这个更新的过程中加入\(k\)的限制。
若\(dis[i][j]\)是由\(dis[i][l]+dis[l][j]\)更新而来的，那么在这种情况下\(i\)到\(j\)的经过边数就是\(i\)到\(l\)的经过边数与\(l\)到\(j\)的经过边数的总和。
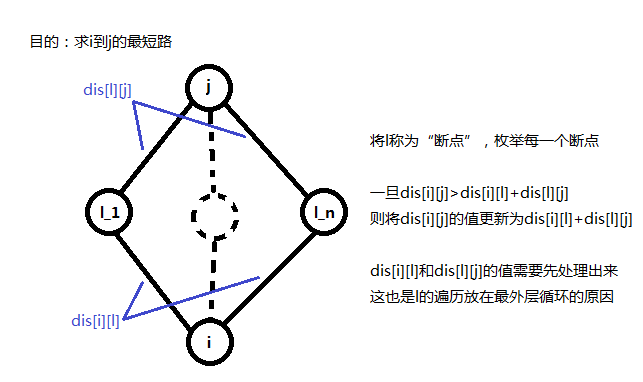
那\(i\)到\(j\)可能的经过的边数就可以通过\(i\)到\(l\)与\(l\)到\(j\)可能经过的边数更新。我们的方法是，外层循环从\(1\)到\(k\)枚举\(i\)到\(l\)可能经过的边数\(p1\)，内层循环从\(1\)枚举\(l\)到\(j\)可能经过的边数\(p2\)，且\(p1+p2<=k\).
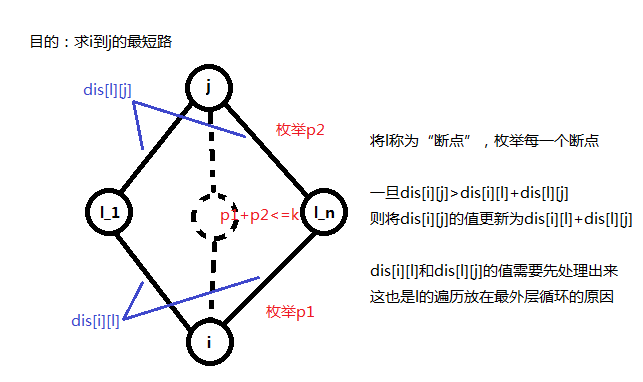
k=minn(k,n);
for(int l=1;l<=n;l++)//l枚举断点
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)//floyd标志性的三层for循环
{
for(int p1=1;p1<=k;p1++)//i到l可能的边数
{
for(int p2=1;p2<=k&&p1+p2<=k;p2++)//l到j可能的边数
{
dis[i][j][p1+p2]=minn(dis[i][j][p1+p2],dis[i][l][p1]+dis[l][j][p2]);
}
}
}
}
}
然后我们便得到了从点\(i\)到点\(j\)，经过\(1~k\)条边的最短路。然后我们再用\(ans[i][j]\)处理出这经过\(1~k\)条边的方案中最短的情况。（即最短路中的最短路）
综合以上两种情况，\(ans[i][j]\)就是最终的最短路了。
如果想用以下代码AC，需要做好常数优化，比如\(O2\),\(register\)...
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int inf=1e9;
const int N=75;
int n,m,a,b,t;
int k,q,c,d;
int dis[N][N][N];//dis[i][j][k]:经过k条边的前提下，i到j的最短路
int ans[N][N];
int minn(int a,int b)
{
return a<b?a:b;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int k=1;k<=n;k++)
dis[i][j][k]=1e9;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
ans[i][j]=1e9;
for(int i=1;i<=n;i++)
for(int k=1;k<=n;k++)
dis[i][i][k]=0;
for(int i=1;i<=n;i++)
ans[i][i]=0;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&a,&b,&t);
dis[a][b][1]=minn(dis[a][b][1],t);
ans[a][b]=minn(ans[a][b],t);
}
scanf("%d%d",&k,&q);
if(k>=n)
{
for(int l=1;l<=n;l++)//l枚举断点
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)//floyed标志性的三层for循环
{
ans[i][j]=minn(ans[i][j],ans[i][l]+ans[l][j]);
//ans[i][j]根据floyed算法的定义，为i到j的最短路
}
}
}
}
else
{
k=minn(k,n);
for(int l=1;l<=n;l++)//l枚举断点
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)//floyed标志性的三层for循环
{
for(int p1=1;p1<=k;p1++)//i到l可能的边数
{
for(int p2=1;p2<=k&&p1+p2<=k;p2++)//l到j可能的边数
{
dis[i][j][p1+p2]=minn(dis[i][j][p1+p2],dis[i][l][p1]+dis[l][j][p2]);
}
}
}
}
}
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
ans[i][j]=inf;
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
for(int l=1;l<=k;l++)
ans[i][j]=minn(ans[i][j],dis[i][j][k]);
}
for(int i=1;i<=q;i++)
{
scanf("%d%d",&c,&d);
if(c==d) puts("0");
else if(ans[c][d]==inf) puts("-1");
else printf("%d\n",ans[c][d]);
}
return 0;
}
继续考虑，若我们能优化掉一层循环，是不是就可以更安稳地A掉这道题了？
依然是以\(k\)作为突破口，有以下策略：“\(k\)越大，答案一定不会更差。”现在我们要利用这种策略，那么上文“令\(dis[i][j][k]\)表示经过\(k\)条边的前提下，\(i\)到\(j\)的最短路”的定义就不合适了。因为我们并不一定要把\(k\)条边走完，\(k\)只是我们做选择时的限制。\(k\)越大，说明限制越宽松。
那么我们的解法便初具雏形了。最外层从\(2\)到\(k\)枚举每一种最大经过的边限制，（为什么不从\(1\)开始枚举？因为最多经过一条边就是相邻两点间的距离了）在循环内跑一个\(floyd\)，总共四层循环。
剩下的问题就是，转移方程如何设计。首先我们需要明确一点：\(k\)越大，说明选择的面更广，所以每一次的答案，是从上一次的答案加上“新的选择”生成的。
b[i][j]=minn(b[i][j],a[i][l]+init[l][j]);
这就是核心转移方程，其中\(b\)数组记录下一次的答案，\(a\)数组记录这一次的答案，\(init\)数组是我们最开始输入的图，它正代表着“新的选择”。
为了维护这个转移方程，首先我们要把输入的图记录下来——\(init\)数组在后续是不会改变的；然后用\(a,b\)两个数组记录这次的结果和下次的结果。具体地讲，就是每轮循环开始时将\(a\)赋给\(b\)，跑完\(floyd\)后再将\(b\)赋给\(a\)，如此往复。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=75;
const int inf=1e9;
int n,m,u,v,t;
int k,q,c,d;
int init[N][N],a[N][N],b[N][N];
int minn(int a,int b)
{
return a<b?a:b;
}
int main()
{
scanf("%d%d",&n,&m);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
init[i][j]=inf;//init数组初始化为一个极大值
for(int i=1;i<=n;i++)
init[i][i]=0;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&t);
init[u][v]=minn(init[u][v],t);
}
scanf("%d%d",&k,&q);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=init[i][j];//a数组最开始的状态就是init
k=minn(k,n);//同理，每个点最多到一次，所以和n取最小
for(int p=2;p<=k;p++)
{
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
b[i][j]=a[i][j];//a赋给b
for(int l=1;l<=n;l++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
b[i][j]=minn(b[i][j],a[i][l]+init[l][j]);//核心：floyd
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
a[i][j]=b[i][j];//b赋给a
}
for(int i=1;i<=q;i++)
{
scanf("%d%d",&c,&d);
if(c==d) puts("0");
else if(a[c][d]==inf) puts("-1");
else printf("%d\n",a[c][d]);
}
return 0;
}
还可以更快吗？
注意到转移方程:
b[i][j]=minn(b[i][j],a[i][l]+init[l][j]);
因为该转移满足结合律，所以考虑用广义矩阵快速幂优化。再想，上个方法的最外层循环是不是在枚举\(k\)？那么，这个转移从本质上来讲就是求\(init[l][j]^k\).
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
using namespace std;
const int N=75;
const int inf=0x3f3f3f3f;//为了方便memset的使用，inf不可以开成1e9
int n,m,u,v,t;
int x,q,c,d;
int init[N][N];
int ans[N][N];
int minn(int x,int y)
{
return x<y?x:y;
}
void mul(int a[N][N],int b[N][N])//矩阵乘法，仔细观察会发现转移方程像极了floyd
{
int c[N][N];
memset(c,inf,sizeof(c));
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
c[i][j]=minn(c[i][j],a[i][k]+b[k][j]);
memcpy(a,c,sizeof(c));
}
int main()
{
scanf("%d%d",&n,&m);
memset(init,inf,sizeof(init));
for(int i=1;i<=n;i++) init[i][i]=0;
for(int i=1;i<=m;i++)
{
scanf("%d%d%d",&u,&v,&t);
init[u][v]=minn(init[u][v],t);
}
scanf("%d%d",&x,&q);
x=minn(x,n);
memset(ans,inf,sizeof(ans));
for(int i=1;i<=n;i++) ans[i][i]=0;
while(x)//矩阵快速幂
{
if(x&1) mul(ans,init);
mul(init,init);
x>>=1;
}
for(int i=1;i<=q;i++)
{
scanf("%d%d",&c,&d);
if(ans[c][d]==inf) puts("-1");
else printf("%d\n",ans[c][d]);
}
return 0;
}
Autobus 方法记录的更多相关文章
- EF里查看/修改实体的当前值、原始值和数据库值以及重写SaveChanges方法记录实体状态
本文目录 查看实体当前.原始和数据库值:DbEntityEntry 查看实体的某个属性值:GetValue<TValue>方法 拷贝DbPropertyValues到实体:ToObject ...
- 64位 SQL Server2008链接访问Oracle 过程汇总解决方法记录
64位 SQL Server2008链接访问Oracle 过程汇总解决方法记录 经过几天不停的网上找资料,实验,终于联通了. 环境:系统:win 2008 ,SqlServer2008 R2, 连接O ...
- js实用方法记录-js动态加载css、js脚本文件
js实用方法记录-动态加载css/js 附送一个加载iframe,h5打开app代码 1. 动态加载js文件到head标签并执行回调 方法调用:dynamicLoadJs('http://www.yi ...
- js实用方法记录-简单cookie操作
js实用方法记录-简单cookie操作 设置cookie:setCookie(名称,值,保存时间,保存域); 获取cookie:setCookie(名称); 移除cookie:setCookie(名称 ...
- js实用方法记录-指不定哪天就会用到的js方法
js实用方法记录-指不定哪天就会用到的js方法 常用或者不常用都有 判断是否在微信浏览器中 测试代码:isWeiXin()==false /** * 是否在微信中 */ function isWeix ...
- Java给各个方法记录执行时间
Java给各个方法记录执行时间 long startTime = System.currentTimeMillis();...//要测试时间的方法LoggerFactory.getLogger(Bas ...
- make menuconfig error 解决方法记录
新建的一个虚拟机,发现make menuconfig 后会出错,查了一下是缺少一些库. 这个错误已经错了两次了,我不希望第三次出现了还想不起来,所以特此记录. # 错误信息: make[2]: *** ...
- 简单一键CENTOS6 安装PPTP VPN方法记录
申明:我们使用PPTP VPN仅仅只能用在查阅资料等正规渠道,不要用在不良用途上.方法收集于网上,这里我用在搬瓦工VPS(VPS方案直达),采用的是CENTOS6 64位系统.我们需要预先将VPS服务 ...
- ASP.NET页面优化性能提升方法记录
今天与大家分享:一种优化页面执行速度的方法.采用这个方法,可以使用页面的执行速度获得[8倍]的提升效果. 为了让您对优化的效果有个直观的了解,我准备了下面的测试结果截图: 测试环境:1. Window ...
随机推荐
- 学习nginx的一点记录
一.nginx定义 Nginx是一款轻量级的.高性能的,具备HTTP.反向代理.负载均衡的web服务器,同时还提供IMAP/POP3/SMTP服务,其特点是占用内存少,并发能力强. 二.nginx基本 ...
- Spring 请求方法的调用原理（Controller）和请求参数的获取的原理
1.请求映射原理 所有的请求都会经过DispatcherServlet这个类,先了解它的继承树 本质还是httpServlet 原理图 测试 request请求携带的参数 从requestMapp ...
- [题解]Balance
1.题目 POJ-1837 2.题目大意 一个天平上有一些钩子,现在有一些砝码.给出每个钩子到原点(姑且这么叫吧)的距离(-15 ~ 15,负数代表在左边,正数相反)以及砝码的重量(1 ~ 20),求 ...
- java-引用数组、继承、super关键字
1.引用类型数组: 1) Cell[] cells = new Cell[4]; cells[0] = new Cell(2,5); cells[1] = new Cell(2,6); cel ...
- Jenkins初始化界面一直显示Please wait while Jenkins is getting ready to work ...
第一次访问jenkins时,会提示如下界面: 注:如果这个界面初始化的时间过长,则需要修改相关配置文件. 原因:因为访问官网太慢.我们只需要换一个源,不使用官网的源即可. 1.找到 jenkins工 ...
- scratch制作彩虹猫病毒模拟器
scratch制作彩虹猫病毒模拟器 hello,大家好. 编程慢慢更加接近生活,甚至小孩也开始学了,比如scratch编程,小编今天就带了一件作品(彩虹猫病毒模拟器) 我们先看一下效果| 做的还可以, ...
- java基础———break，continue
break通常用在循环语句之中用来跳出循环: continue终止某次循环过程,跳过尚未执行的语句:接着执行下次是否执行循环的判定:
- 快速生成组件语法模板的插件:Auto Close Tag
好家伙, 这是一个"标签闭合"插件 Auto Close Tag的安装: 来到VScode的拓展 安装后, 在其中输入一个左标签符号"<",随后会出现提示 ...
- 百度松果菁英班OJ【连载】
第十六周 2 的 n 次幂 高精度乘法 #include<bits/stdc++.h> using namespace std; vector<int> mul(vector& ...
- Python中None作为索引的作用
None的作用主要是在使用None的位置新增一个维度. a = np.arange(25).reshape(5,5) print(a) ''' [[ 0 1 2 3 4] [ 5 6 7 8 9] [ ...