CTFshow——funnyrsa2

题目如下：

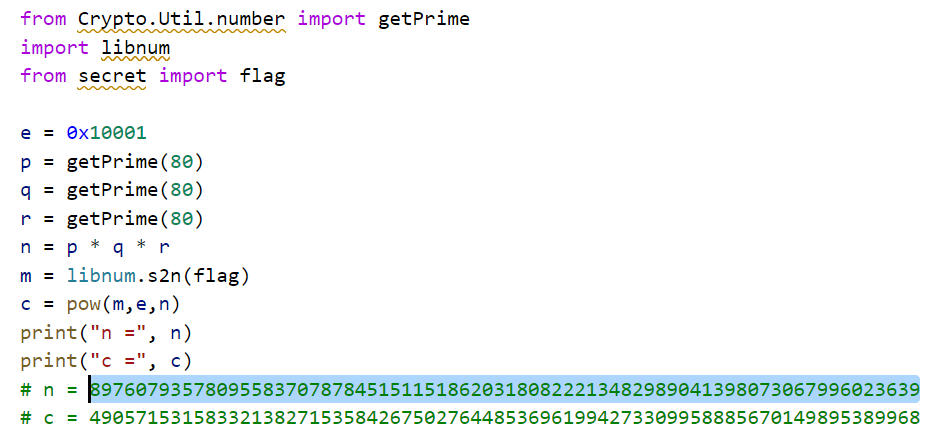
题目分析：

发现n很小，可以考虑yafu分解n，或者使用在线网站，例如：http://factordb.com/。即得p，q，r。因为常规rsa只有p和q，则phi = (p -1) * (q - 1)，而现在有3个因子，所以phi = (p - 1) * (q - 1) * (r - 1)。

phi = (p - 1) * (q - 1) * (r - 1)的原因：

根据欧拉函数，如果存在n可以分解成两个互质的整数之积，即

　　n = p1 * q1

则存在这样的关系：

　　phi(n) = phi(p1*q1) = phi(p1) * phi(q1) = （p1 - 1）* (q1 - 1)

举个例子：

n = 56，则phi(56) = phi(8 * 7) = phi(8) * phi(7) = 4 * 6 =24

求解phi(8) 即是求1到8之中有多少个与8互质的数？分别为1,3,5,7。同理得到phi(7)=6，即1,2,3,4,5,6都与7互质。

根据以上即知原因

脚本编写：

from Cryptodome.Util.number import *
import gmpy2

n = 897607935780955837078784515115186203180822213482989041398073067996023639
c = 490571531583321382715358426750276448536961994273309958885670149895389968
e = 0x10001
p = 876391552113414716726089
q = 932470255754103340237147
r = 1098382268985762240184333

phi = (p - 1) * (q - 1) * (r - 1)
t = gmpy2.gcd(e, phi)
#print(t)
d = gmpy2.invert(e, phi)
#print(d)
m = pow(c, d, n)
#print(m)
print(long_to_bytes(m))

总结：

n分解出的因子大于2个的情况下的解法