Cesium中各种坐标以及相互转换(七)

2023-01-11

1.坐标系

Cartesian3

笛卡尔坐标，又叫世界坐标，是一个三维空间中的点，具有xyz，类似：(-1314910.6675027965, 5328726.846411945, 3238183.748823095)，单位为米

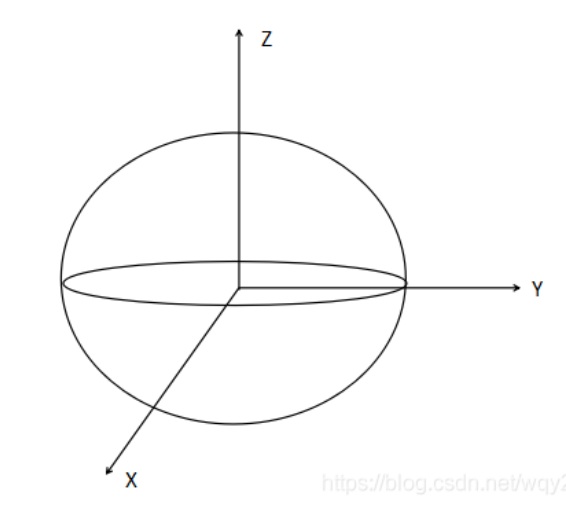
原点在椭球中心

Cartesian2

是二维空间中的点，通常是屏幕坐标

console.log(`鼠标点击位置为:${click.position}`);

鼠标点击位置为:(372.79998779296875, 213.7999997138977)

屏幕左上角为原点，向右为x正方向，向下为y正方向

cartographic

和Cartesian3一样是三维空间中的点，但是单位是弧度，通常也叫椭球坐标

当世界坐标为:(-1315009.0349616667, 5329125.484381694, 3238427.62747913)，

此时对应的cartographic为:(1.8127222052449903, 0.5359692831389684, 492.5617098962376)

第三个参数是海拔，单位为米。

经纬度

Cesuim中没有具体的经纬度对象，要得到经纬度首先需要计算为弧度，再进行转换。

2.坐标转换

2.1 转换为经纬度

其实在实际应用中最常用的就是经纬度，我们先将如何转换为经纬度

2.1.1 cartographic 转经纬度（弧度转经纬度）

这是最简单的，弧度和经纬度是可以直接按照数学公式计算的。

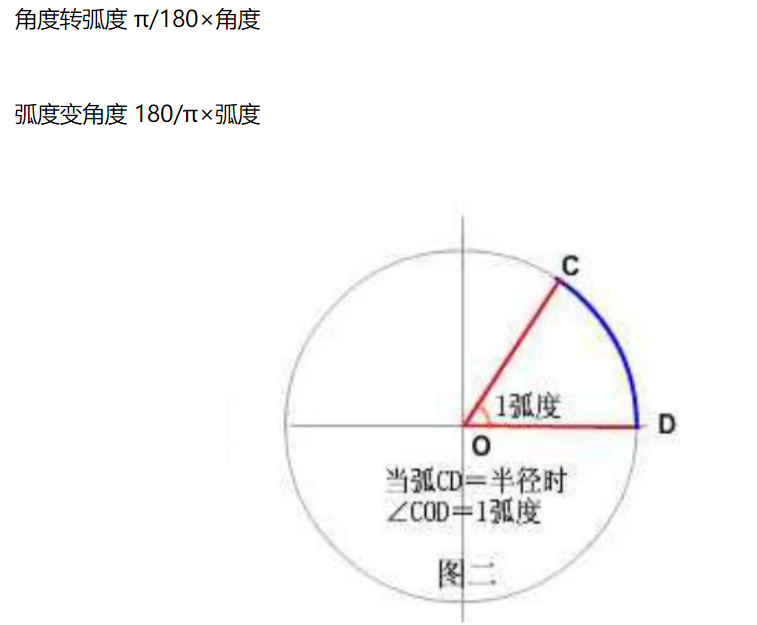
Cesium的Math库也提供了函数进行计算：

          // 弧度转换为经纬度

          var lon = Cesium.Math.toDegrees(cartographic.longitude);  // 经度

          var lat = Cesium.Math.toDegrees(cartographic.latitude);   // 纬度

          console.log(`经度：${lon},纬度:${lat}`);

2.1.2 Cartesian3转经纬度（世界坐标/笛卡尔坐标转经纬度）

由于已经知道如果有弧度的话就可以计算得到经纬度，所以问题转换为如何将世界坐标转换为椭球坐标。

找到了如下方法

可以直接用Cartesian3创建一个弧度坐标。

          var x = Cesium.Cartographic.fromCartesian(new Cesium.Cartesian3.fromDegrees(100,30,500))

          console.log(`100,30,500对应的弧度:${x}`);

100,30,500对应的弧度:(1.7453292519943295, 0.5235987755982987, 499.9999999999014)

2.1.3 屏幕坐标转经纬度

在camera里有这么一个方法

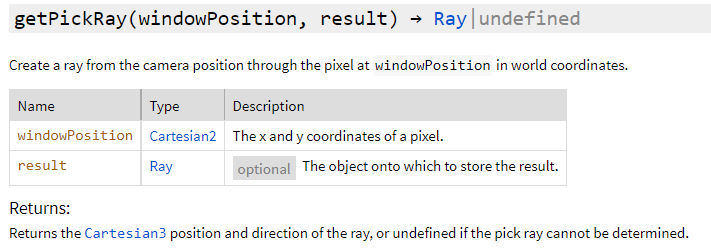
返回一个Cartesian3也就是笛卡尔坐标系下的点

click是点击事件，这里不用管

          console.log(`鼠标点击位置为:${click.position}`);

          var cartesian = that.viewer.scene.globe.pick(that.viewer.camera.getPickRay(click.position),that.viewer.scene);

          console.log(`世界坐标:${cartesian}`);

鼠标点击位置为:(367.20001220703125, 233.00003337860107)

世界坐标:(-1296852.0512911458, 5257755.129365052, 3210992.6158761424)

Cartesian3怎么转经纬度不用说了吧

           //转换为弧度

          var x = Cesium.Cartographic.fromCartesian(cartesian);

          console.log(x);

          //弧度转经纬度

          var lon = Cesium.Math.toDegrees(cartographic.longitude);  // 经度

          var lat = Cesium.Math.toDegrees(cartographic.latitude);   // 纬度

          console.log(`经度：${lon},纬度:${lat}`);

2.2 经纬度转换为其他

2.2.1 经纬度转换为弧度

          //经纬度转弧度

          var cartographic=Cesium.Cartographic.fromDegrees(lon,lat,height);

          console.log(cartographic);

2.2.2 经纬度转换为世界坐标

Cesium.Cartesian3.fromDegrees(longitude, latitude, height, ellipsoid, result);

很明显，fromDegrees这个方法就是从经纬度转换为某某坐标系下的方法

2.2.3 经纬度转换为屏幕坐标

          var c3 = Cesium.Cartesian3.fromDegrees(new Cesium.Cartesian3(100,30,500));

          //笛卡尔坐标转屏幕坐标

          var c2 = Cesium.SceneTransforms.wgs84ToWindowCoordinates(that.viewer.scene, c3);

          console.log(c2);

原点是viewer的原点

3. 总结

我们可以画一条线

Cartesian2 -> Cartesian3 -> cartographic -> 经纬度

这条线往返转换的方法都讲了，依次转换就可以了

中间应该还有一些跳步骤的方法，比如Cesium.Cartesian3.fromDegrees(longitude, latitude, height, ellipsoid, result)，经纬度直接转换为世界坐标

后面再更新