【Note】（坑）一些组合恒等式的实际意义理解（和待填坑的组合数学知识）

- 排列组合
- 恒等式
(1) $C_n^m=C_n^{n-m}$
(2) $A_n^m+mA_n^{m-1}=A_{n+1}^m$
(3) $C_n^{m-1}+C_n^{m}=C_{n+1}^m \ or \ C_{n-1}^{m-1}+C_{n-1}^m=C_n^m$
(3*) $\sum_{i=m}^nC_i^m=C_m^m+C_{m+1}^m+C_{m+2}^m+\cdots+C_{n-1}^m+C_n^m=C_{n+1}^{m+1}$
(4) $C_n^{m-1}+2C_n^m+C_n^{m+1}=C_{n+2}^{m+1}$
(5) $C_a^b \times C_b^c=C_a^c \times C_{a-c}^{b-c}=C_a^c \times C_{a-c}^{a-b}$
(6) $\sum_{i=0}^{a}C_n^iC_m^{a-i}=C_n^0C_m^a+C_n^1C_m^{a-1}+\cdots+C_n^{a-1}C_m^1+C_n^aC_m^0=C_{n+m}^a$

排列组合

\[{n \choose m} = \frac{n!}{(n-m)!m!}
\]

\[A_n^m=\frac{n!}{(n-m)!}
\]

\[C_n^m=\frac{A_n^m}{A_m^m}=\frac{n!}{(n-m)!m!}
\]

恒等式

(1) $C_n^m=C_n^{n-m}$

从$n$个元素选择$m$个，等价于$n$个元素中不选$n-m$个。

(2) $A_n^m+mA_n^{m-1}=A_{n+1}^m$

在$n+1$个元素中选择$m$个元素排成一排，等价于考虑第$n+1$个元素：

不在该排列中：$A_n^m$
存在该排列中：$mA_n^{m-1}$，$m$表示该元素有$m$种放置位置。

(3) $C_n^{m-1}+C_n^{m}=C_{n+1}^m \ or \ C_{n-1}^{m-1}+C_{n-1}^m=C_n^m$

在$n+1$个元素中选出$m$个元素，等价于考虑第$n+1$个元素：

不在该组合中：$C_n^m$
存在该组合中：$C_n^{m-1}$

(3*) $\sum_{i=m}^nC_i^m=C_m^m+C_{m+1}^m+C_{m+2}^m+\cdots+C_{n-1}^m+C_n^m=C_{n+1}^{m+1}$

可由式$(3)$推导而出。

$C_{m+1}^{m+1}=1=C_{m}^{m}$

$C_{m}^{m}+C_{m+1}^{m}=C_{m+1}^{m+1}+C_{m+1}^m=C_{m+2}^{m+1}$

$C_{m+2}^{m+1}+C_{m+2}^m=C_{m+3}^{m+1}$

$\cdots$

$C_{n}^{m+1}+C_n^m=C_{n+1}^{m+1}$

得证。

事实上式$(3)$可以认为是在杨辉三角上的递推。所以该式也可以由杨辉三角进行理解（如图）。

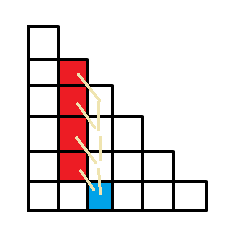
事实上很多恒等式都可以直接利用杨辉三角进行（眼睛上的）理解推导（）

(4) $C_n^{m-1}+2C_n^m+C_n^{m+1}=C_{n+2}^{m+1}$

从$n+2$个元素中选出$m+1$个元素，考虑第$n+1$个元素和第$n+2$个元素：

两元素都不在该组合中：$C_n^{m+1}$
两元素都在该组合中：$C_n^{m-1}$
两元素有一个在该组合中：$2C_n^m$

(5) $C_a^b \times C_b^c=C_a^c \times C_{a-c}^{b-c}=C_a^c \times C_{a-c}^{a-b}$

考虑在集合$A'$，$|A'|=a$中，求构造集合$C' \subseteq B' \subseteq A'$，$|C'|=c,|B'|=b$的方案数。

先从$A'$中$a$个元素中取出$b$个元素放入$B'$，再从$B'$中取出$c$个元素放入$C'$：$C_a^b \times C_b^c$
先从$A'$中$a$个元素中取出$c$个元素放入$C'$（当然同时也放进了$B '$），再从剩下的$a-c$个元素中取出$b-c$个元素放入$\complement_{B'}C'$中：$C_a^c \times C_{a-c}^{b-c}$

(6) $\sum_{i=0}^{a}C_n^iC_m^{a-i}=C_n^0C_m^a+C_n^1C_m^{a-1}+\cdots+C_n^{a-1}C_m^1+C_n^aC_m^0=C_{n+m}^a$

在$n+m$个元素中选出$a$个元素：

前$n$个元素中选择了$i$个元素，后$m$个元素中选择了$a-i$个元素：$C_n^iC_m^{a-i}$

特别地，当$m=n$时：

$\sum_{i=0}^aC_n^iC_n^{a-i}=C_{2n}^a$

又根据$C_n^i=C_n^{n-i}$，当$a=n$时：

$\sum_{i=0}^n(C_n^i)^2=C_{2n}^n$

多重集合（全）排列数

设可重集$S=\{n_1 \cdot a_1,\cdots,n_k \cdot a_k \}$

$S$的全排列数为：

$$\frac{n!}{n_1! \cdots n_k!}$$

将$m$个相同物品放入$n$个相同盒子 || 将正整数$m$划分成$n$个正整数的和

1.当作容量为$n$，物品大小为$1 \dots m$的完全背包。

2.设$f_{i,j}$表示将正整数$i$划分为$j$个正整数之和的方案数：$f_{i,j}=f_{i-1,j-1}+f_{i,j-i}$

Catalan数

一些等价的Catalan数相关问题例：

入栈序列为$1 \dots n$的出栈序列种数；
（基本模型）将$n$个$0$和$n$个$1$排成任意前缀$0$的个数不少于$1$的个数的序列数量；
$n$个左括号和$n$个右括号组成的合法括号序列个数；
$n$个节点构成的不同二叉树数量；
平面直角坐标系中从原点$(0,0)$出发到$(2n,0)$，每一步可以向正右上或正右下移动，并且路径不经过第四象限的方案数
$\dots$

使用例$(3)$来说明，对$n$个节点构成二叉树数量的一种$(0)$的理解：入栈后继续入栈为左儿子，直接出栈为没有左儿子；出栈后入栈为右儿子，直接出栈为没有右儿子。

其实这个问题的原本理解是：已知先序遍历，求构造中序遍历的方案数。

当然也可以理解为一个递推：设$Cat_i$表示$i$个节点构成二叉树的数量，那么有$Cat_i=\sum_{j=0}^i Cat_j \times Cat_{i-j}$

现在用例$(4)$来说明：

平面直角坐标系中从原点$(0,0)$出发到$(2n,0)$，每一步可以向正右上或正右下移动，并且路径不经过第四象限的方案数

也即有$n$个向右上的操作，$n$个向右下的操作。

可以考虑用所有的方案（$C_{2n}^n$）减去不合法的（经过第四象限的方案）

每个不合法的方案必定经过直线$y=-1$。将这样每个方案第一个与该直线相交的点之后的整段路径，会得到唯一对应的一条终点为$(2n,-2)$的路径。

也就是从$(0,0)$到$(2n,-2)$的每一条路径都对应了一条原问题不合法的路径。

所以答案即$Cat_n=C_{2n}^n-C_{2n}^{n-1}$

zzx：另外还有$Cat_n=\frac{C^{n}_{2n}}{n+1}$