Codeforces Round #801 (Div. 2) and EPIC Institute of Technology Round

C - Zero Path

在这道题目中，不可以真正地进行寻找必须另想办法。

  1. 考虑到只能向右面还有下面走，所以对于一个点，它只可能有已经走过的点转移过来，这让我想起来动态规划。
  2. 动态规划考虑最优解，这里所需要求的是0，不可以直接考虑是否与0相接近，需要考虑其他解法。
  3. 最大值以及最小值是唯一的，所以可以通过动态规划，最终求出目的地的最大数字以及最小数字。
  4. 证明题目结论的充分必要条件。
  5. 如果最小值都大于0 || 最大值都小于0，那么就不行。
  6. 如果m+n-1（即所有要走过的1或者-1的个数），如果m+n-1 是奇数，那么就肯定不可能加起来等于0
  7. 如果m+n-1是偶数，并且最小值小于等于0，最大值大于等于0。
  8. 根据7中的m+n-1是偶数，得知最大值以最小值一定是偶数（不妨设路径上全部都是1，那么最大值一定是偶数，考虑替换其中的1为-1，同样也是偶数）。

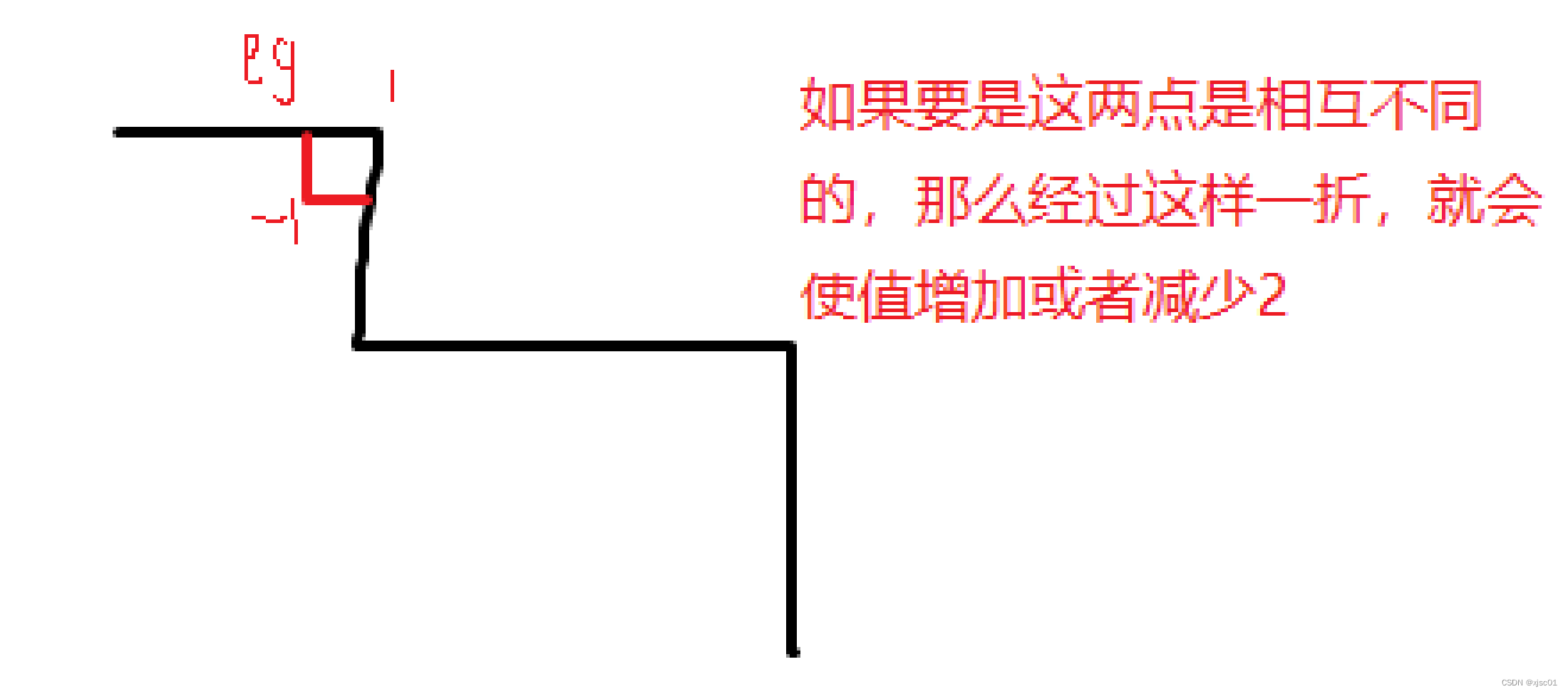
  9. 10.最后的到的值最大的路以及值最小的路的路径总可以通过一点一点变化2达到对方。故一定有一条路可以使路径上的值相加为0.

D2-Tree Queries (Hard Version)

D1和D2除了数据之外，没有什么不同

Codeforces Round #801 (Div. 2) and EPIC Institute of Technology Round（C，D题解）的更多相关文章

  1. Codeforces Round #801 (Div. 2) C(规律证明)

    Codeforces Round #801 (Div. 2) C(规律证明) 题目链接: 传送门QAQ 题意: 给定一个\(n * m\)的矩阵,矩阵的每个单元的值为1或-1,问从\((1,1)\)开 ...

  2. Codeforces Round #517 (Div. 2, based on Technocup 2019 Elimination Round 2)

    Codeforces Round #517 (Div. 2, based on Technocup 2019 Elimination Round 2) #include <bits/stdc++ ...

  3. Codeforces Round #801 (Div. 2)

    题集链接 A Subrectangle Guess 代码 #include <bits/stdc++.h> #define endl "\n" using namesp ...

  4. (AB)Codeforces Round #528 (Div. 2, based on Technocup 2019 Elimination Round

    A. Right-Left Cipher time limit per test 1 second memory limit per test 256 megabytes input standard ...

  5. Codeforces Round #596 (Div. 2, based on Technocup 2020 Elimination Round 2)

    A - Forgetting Things 题意:给 \(a,b\) 两个数字的开头数字(1~9),求使得等式 \(a=b-1\) 成立的一组 \(a,b\) ,无解输出-1. 题解:很显然只有 \( ...

  6. Codeforces Round #434 (Div. 2, based on Technocup 2018 Elimination Round 1)&&Codeforces 861C Did you mean...【字符串枚举，暴力】

    C. Did you mean... time limit per test:1 second memory limit per test:256 megabytes input:standard i ...

  7. Codeforces Round #434 (Div. 2, based on Technocup 2018 Elimination Round 1)&&Codeforces 861B Which floor?【枚举，暴力】

    B. Which floor? time limit per test:1 second memory limit per test:256 megabytes input:standard inpu ...

  8. Codeforces Round #434 (Div. 2, based on Technocup 2018 Elimination Round 1)&&Codeforces 861A k-rounding【暴力】

    A. k-rounding time limit per test:1 second memory limit per test:256 megabytes input:standard input ...

  9. Codeforces Round #543 (Div. 2, based on Technocup 2019 Final Round)

    A. Technogoblet of Fire 题意:n个人分别属于m个不同的学校 每个学校的最强者能够选中 黑客要使 k个他选中的可以稳被选 所以就为这k个人伪造学校 问最小需要伪造多少个 思路:记 ...

随机推荐

  1. 一文带你速懂虚拟化KVM和XEN

    来源 :蛋蛋团 前言 "云计算"这个技术经过十余年的普及到如今已经可以称得上是家喻户晓了,基于云计算平台,在多个领域内创造了一个又一个的记录:电子商务里亿万人同时在线抢购的的&qu ...

  2. git提交代码到GitHub操作-简易版（后续完善）

    一.git上传代码到GitHub 1.远程仓库GitHub创建好一个新仓库注意仓库名 2.本地建一个目录写代码,目录名与仓库命名一致 3.在目录下右键 git Bash here 打开git终端命令行 ...

  3. 你不知道的JS 中——yield

    <!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...

  4. HCNP Routing&Switching之RSTP

    前文我们了解了vlan优化,vlan聚合技术super vlan相关话题,回顾请参考https://www.cnblogs.com/qiuhom-1874/p/16208997.html:今天我们来聊 ...

  5. EditText简单登陆界面制作

  6. 【FineBI】增量数据更新语句

    SELECT * FROM t_abike_user WHERE AddUserTime BETWEEN '2016-11-17 10:49:04' AND '2021-07-31 23:59:59'

  7. 【FineBI】FineBI连接阿里云mysql教程

    因为某些原因需要查看数据信息,之前连接成功一次,今天软件更新了以后发现连接信息丢. 又重新折腾了一下. 主要有2个地方: 1.查看阿里云数据库外网连接地址:打开云数据库RDS-实例列表-管理-数据库连 ...

  8. 利用 Onekey Theater 改善屏幕显示效果

    介绍 Onekey Theater(一键影音),它是联想笔记本带的一键影音功能,使用它能够更改笔记本的显示效果和音效,以此模仿电影院的效果,为用户带来更好是视听效果及享受. 作用 之前的联想笔记本自带 ...

  9. 记一次Tomcat卡死在 Deploying web application 步骤的问题

    公司有一个历史的遗留项目是传统的MVC架构的前后不分离的项目,一开始使用JDK1.7写的,后来前一阵老板说想在这个远古项目上加点功能,顺带换换皮,于是乎一帮程序员们就用JDK1.8重新翻新了一遍项目顺 ...

  10. 什么事JAVA

    1.什么是Java Java是一门面向对象的高级编程语言,不仅吸收了C++语言的各种优点,比如继承了C++语言面向对象的 技术核心.还摒弃了C++里难以理解的多继承.指针等概念,,同时也增加了垃圾回收 ...