P/NP问题

目录

　　P

　　NP

　　NPC

　　NPH

写在开头

　　1、多项式

　　　　如公式：y = axⁿ-bx^n-1+c。Ο(log₂n)、Ο(n)、 Ο(nlog₂n)、Ο(n²)和Ο(n³)称为多项式时间。Ο(2ⁿ)和Ο(n!)称为指数时间。

　　2、时间复杂度

　　　　度量程序随问题规模n的变化而变化所消耗的时间。

P

　　P：polynominal，多项式。存在多项式时间算法的问题。

NP

　　NP：Nondeterministic polynominal，非确定性多项式。能在多项式时间内验证得出一个正确解的问题。上面指数时间的算法可以看成NP问题。

　　P类问题是NP问题的子集，因为存在多项式时间解法的问题，总能在多项式时间内验证他。

　　问题：是否 NP类问题=P类问题？

　　答案：不确定，有的是，有的不是。

NPC

　　NPC：NP complete又叫NP完全问题。如果该np问题都能在多项式时间内转化为NPC，则称该np问题为npc问题。

　　NPC问题是NP问题的子集。

　　当然，很多时候NPC问题是找不到一个多项式时间算法的，更多时候他是一个指数级的算法。

NPH

　　NPH：NP hard问题。它不是一个NP问题，然后所有的NPC问题都可以在多项式时间内转化为NPH的话，我们就叫他NPH（hard）问题。

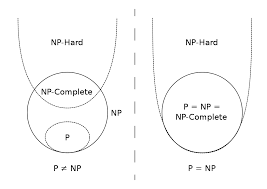
四者关系：如图