tensorflow中一个矩阵和一个向量相加
import tensorflow as tf x=tf.constant([[1,2],[3,4]])
y=tf.constant([[1],[1]])#列向量
z=tf.constant([1,1])#行向量 u=x+y
v=x+z print(u)
print(v)
tensorflow中矩阵可以和矢量相加,
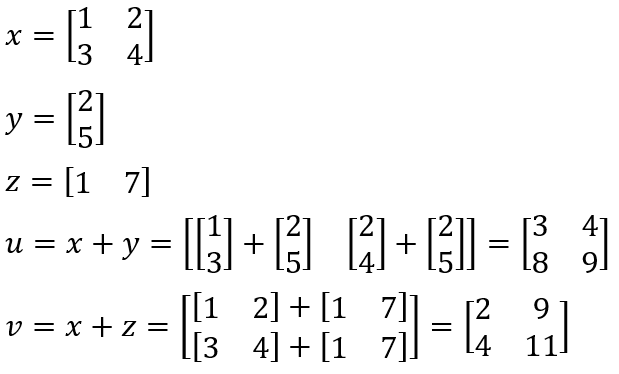
输出结果:
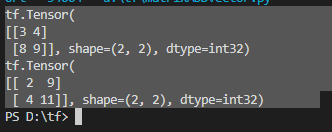
tensorflow中一个矩阵和一个向量相加的更多相关文章
- TensorFlow中的并行执行引擎——StreamExecutor框架
背景 [作者:DeepLearningStack,阿里巴巴算法工程师,开源TensorFlow Contributor] 在前一篇文章中,我们梳理了TensorFlow中各种异构Device的添加和注 ...
- TensorFlow 中的卷积网络
TensorFlow 中的卷积网络 是时候看一下 TensorFlow 中的卷积神经网络的例子了. 网络的结构跟经典的 CNNs 结构一样,是卷积层,最大池化层和全链接层的混合. 这里你看到的代码与你 ...
- IT公司100题-35- 求一个矩阵中最大的二维矩阵(元素和最大)
问题描述: 求一个矩阵中最大的二维矩阵(元素和最大).如: 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 中最大的是: 4 5 9 10 分析: 2*2子数组的最大和.遍历求和,时 ...
- 【TensorFlow随笔】关于一个矩阵与多个矩阵相乘的问题
问题描述: Specifically, I want to do matmul(A,B) where 'A' has shape (m,n) 'B' has shape (k,n,p) and t ...
- py-统计一个矩阵中每一列的非0数的个数
1.文件类型类似于这样: 不过数据量比这个要更大一点. 2.对应上述数据的运行结果: import matplotlib.pyplot as plt with open('test.txt') as ...
- python/numpy/tensorflow中,对矩阵行列操作,下标是怎么回事儿?
Python中的list/tuple,numpy中的ndarrray与tensorflow中的tensor. 用python中list/tuple理解,仅仅是从内存角度理解一个序列数据,而非数学中标量 ...
- Eigen中的矩阵及向量运算
Eigen中的矩阵及向量运算 ,[+,+=,-,-=] ,[\*,\*=] ,[.transpose()] ,[.dot(),.cross(),.adjoint()] ,针对矩阵元素进行的操作[.su ...
- Opencv Surf算子中keyPoints,描述子Mat矩阵,配对向量DMatch里都包含了哪些好玩的东东?
Surf算法是一把牛刀,我们可以很轻易的从网上或各种Opencv教程里找到Surf的用例,把例程中的代码或贴或敲过来,满心期待的按下F5,当屏幕终于被满屏花花绿绿的小圆点或者N多道连接线条霸占时,内心 ...
- LeetCode竞赛题:笨阶乘(我们设计了一个笨阶乘 clumsy:在整数的递减序列中,我们以一个固定顺序的操作符序列来依次替换原有的乘法操作符:乘法(*),除法(/),加法(+)和减法(-)。)
通常,正整数 n 的阶乘是所有小于或等于 n 的正整数的乘积.例如,factorial(10) = 10 * 9 * 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1.相反,我们设计了一个笨 ...
随机推荐
- Spring Cloud(O)服务的注册与发现(Eureka)
一.微服务架构 1.1什么是分布式 不同模块部署在不同服务器上 作用:分布式解决网站高并发带来问题 1.2什么是集群 多台服务器部署相同应用构成一个集群 作用:通过负载均衡设备共同对外提供服务 1.3 ...
- jumperver源码理解以及部分修改
一 admin后台处理以及展示修改 jumpserver 默认不开放admin后台(获取是我没用使用正确的打开方式,) 打开方式 找到程序的入口 urls.py 修改,另外主要看下settin ...
- hadoop中hive的属性
1.在hive中是可以删除文件的: hive> dfs -rm -R /u2.txt > ; Deleted /u2.txt 2.hive 中的default数据库 <propert ...
- 【Distributed】分布式Session一致性问题
一.概述 1.1 什么是Session 1.2 Session实现原理 1.3 Session常见问题 Session 保证在那里? 关闭浏览器Session会失效吗 服务器集群之后,Session产 ...
- 前端基础(五):jQuery
jQuery介绍 jQuery是一个轻量级的.兼容多浏览器的JavaScript库. jQuery使用户能够更方便地处理HTML Document.Events.实现动画效果.方便地进行Ajax交互, ...
- 01_Redis简述
一:关系型数据库和非关系型数据库的区别: 1:关系型数据库(SQL):数据和数据之间,表和字段之间,表和表之间是存在关系的: 优点:数据之间有关系,进行数据的增删改查时非常方便的:关系型数据库有事务操 ...
- JSONObject fromObject() 需要引入的包
1. maven项目 在pom.xml中添加以下依赖: <dependency> <groupId>net.sf.json-lib</groupId> <ar ...
- CentOS7 基于 subversion 配置 SVN server
由于 Window Server 环境下,VisualSVN Server Community 版本只支持 15 个同时在线用户,所以彻底放弃 Windows Server,在 Linux Serve ...
- zabbix内存溢出解决方法
1406:20180802:183248.783 __mem_malloc: skipped 0 asked 48 skip_min 4294967295 skip_max 0 1406:201808 ...
- CF827D Best Edge Weight[最小生成树+树剖/LCT/(可并堆/set启发式合并+倍增)]
题意:一张图求每条边边权最多改成多少可以让所有MST都包含这条边. 这题还是要考察Kruskal的贪心过程. 先跑一棵MST出来.然后考虑每条边. 如果他是非树边,要让他Kruskal的时候被选入,必 ...
