广义线性模型 R--glm函数

R语言glm函数学习： 

【转载时请注明来源】：http://www.cnblogs.com/runner-ljt/

Ljt

作为一个初学者，水平有限，欢迎交流指正。

glm函数介绍：

glm(formula, family=family.generator, data,control = list(...))

family：每一种响应分布（指数分布族）允许各种关联函数将均值和线性预测器关联起来。

常用的family：

binomal(link='logit')         ----响应变量服从二项分布，连接函数为logit，即logistic回归

binomal(link='probit')       ----响应变量服从二项分布，连接函数为probit

poisson(link='identity')     ----响应变量服从泊松分布，即泊松回归

control:控制算法误差和最大迭代次数

glm.control(epsilon = 1e-8, maxit = 25, trace = FALSE)

-----maxit:算法最大迭代次数，改变最大迭代次数：control=list(maxit=100)

glm函数使用：

>
> data<-iris[1:100,]
> samp<-sample(100,80)
> names(data)<-c('sl','sw','pl','pw','species')
> testdata<-data[samp,]
> traindata<-data[-samp,]
>
> lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata)
Warning messages:
1: glm.fit:算法没有聚合
2: glm.fit:拟合機率算出来是数值零或一
> summary(lgst)

Call:
glm(formula = testdata$species ~ pl, family = binomial(link = "logit"),
    data = testdata)

Deviance Residuals:
       Min          1Q      Median          3Q         Max
-1.836e-05  -2.110e-08  -2.110e-08   2.110e-08   1.915e-05  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)   -83.47   88795.25  -0.001    0.999
pl             32.09   32635.99   0.001    0.999

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1.1085e+02  on 79  degrees of freedom
Residual deviance: 1.4102e-09  on 78  degrees of freedom
AIC: 4

Number of Fisher Scoring iterations: 25

>

　　

注意在使用glm函数就行logistic回归时，出现警告：

Warning messages:
1: glm.fit:算法没有聚合
2: glm.fit:拟合機率算出来是数值零或一

同时也可以发现两个系数的P值都为0.999，说明回归系数不显著。

第一个警告：算法不收敛。
     由于在进行logistic回归时，依照极大似然估计原则进行迭代求解回归系数，glm函数默认的最大迭代次数 maxit=25，当数据不太好时，经过25次迭代可能算法 还不收敛，所以可以通过增大迭代次数尝试解决算法不收敛的问题。但是当增大迭代次数后算法仍然不收敛，此时数据就是真的不好了，需要对数据进行奇异值检验等进一步的处理。

>
> lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata,control=list(maxit=100))
Warning message:
glm.fit:拟合機率算出来是数值零或一
> summary(lgst)

Call:
glm(formula = testdata$species ~ pl, family = binomial(link = "logit"),
    data = testdata, control = list(maxit = 100))

Deviance Residuals:
       Min          1Q      Median          3Q         Max
-1.114e-05  -2.110e-08  -2.110e-08   2.110e-08   1.162e-05  

Coefficients:
             Estimate Std. Error z value Pr(>|z|)
(Intercept)    -87.18  146399.32  -0.001        1
pl              33.52   53808.49   0.001        1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 1.1085e+02  on 79  degrees of freedom
Residual deviance: 5.1817e-10  on 78  degrees of freedom
AIC: 4

Number of Fisher Scoring iterations: 26

>

　　

如上，通过增加迭代次数，解决了第一个警告，此时算法收敛。

但是第二个警告仍然存在，且回归系数P=1，仍然不显著。

第二个警告：拟合概率算出来的概率为0或1

首先，这个警告是什么意思？
我们先来看看训练样本的logist回归结果，拟合出的每个样本属于'setosa'类的概率为多少？

>
>lgst<-glm(testdata$species~pl,binomial(link='logit'),data=testdata,control=list(maxit=100))
>p<-predict(lgst,type='response')
>plot(seq(-2,2,length=80),sort(p),col='blue')
>

　                                        

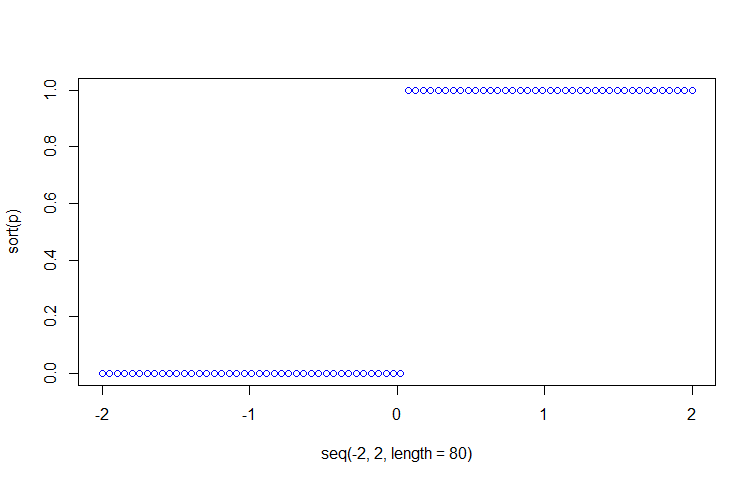
可以看出训练样本为'setosa'类的概率不是几乎为0，就是几乎为1，并不是我们预想中的logistic模型的S型曲线，这就是第二个警告的意思。

那么问题来了，为什么会出现这种情况？
 （以下内容只是本人参考一些解释的个人理解）

这种情况的出现可以理解为一种过拟合，由于数据的原因，在回归系数的优化搜索过程中，使得分类的种类属于某一种类（y=1)的线性拟合值趋于大，分类种类为另一   类(y=0)的线性拟合值趋于小。

由于在求解回归系数时，使用的是极大似然估计的原理，即回归系数在搜索过程中使得似然函数极大化：

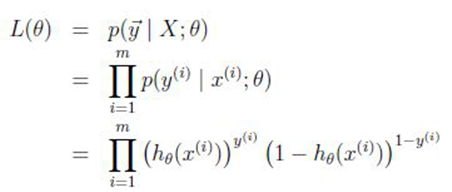
所以在搜索过程中偏向于使得y=1的h(x)趋向于大，而使得y=0的h(x)趋向于小。

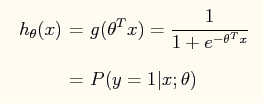
即系数Θ使得 Y=1类的 -Θ^TX 趋向于大，使得Y=0类的 -Θ^TX 趋向于小。而这样的结果就会导致P(y=1|x;Θ)-->1  ； P(y=0|x;Θ)-->0  .

那么问题又来了，什么样的数据会导致这样的过拟合产生呢？

先来看看上述logistic回归中种类为setosa和versicolor的样本pl值的情况。（横轴代表pl值，为了避免样本pl数据点叠加在一起，增加了一个无关的y值使样本点展开）

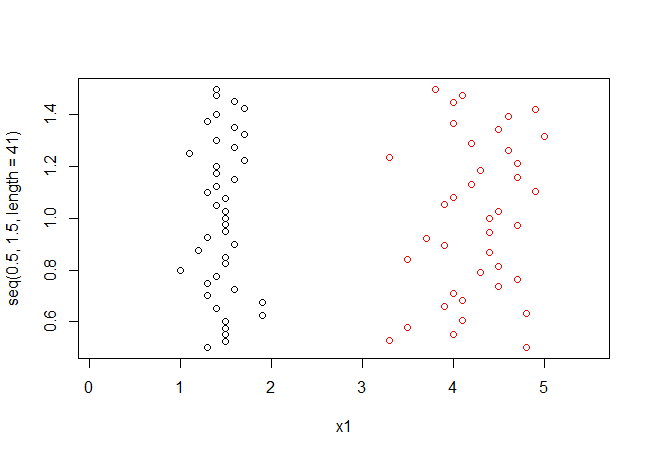
可以看出两类数据明显的完全线性可分。

故在回归系数搜索过程中只要使得一元线性函数h(x)的斜率的绝对值偏大，就可以实现y=1类的h(x)趋向大，y=0类的h(x)趋向小。

所以当样本数据完全可分时，logistic回归往往会导致过拟合的问题，即出现第二个警告：拟合概率算出来的概率为0或1。

出现了第二个警告后的logistic模型进行预测时往往是不适用的，对于这种线性可分的样本数据，其实直接使用规则判断的方法则简单且适用（如当pl<2.5时则直接判断为setosa类，pl>2.5时判断为versicolor类）。

以下，对于不完全可分的二维训练数据展示logistic回归过程。

>
> data<-iris[51:150,]
> samp<-sample(100,80)
> names(data)<-c('sl','sw','pl','pw','species')
> testdata<-data[samp,]
> traindata<-data[-samp,]
>
> lgst<-glm(testdata$species~sw+pw,binomial(link='logit'),data=testdata)
> summary(lgst)

Call:
glm(formula = testdata$species ~ sw + pw, family = binomial(link = "logit"),
    data = testdata)

Deviance Residuals:
     Min        1Q    Median        3Q       Max
-1.82733  -0.16423   0.00429   0.11512   2.12846  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)
(Intercept)  -12.915      5.021  -2.572   0.0101 *
sw            -3.796      1.760  -2.156   0.0310 *
pw            14.735      3.642   4.046 5.21e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 110.85  on 79  degrees of freedom
Residual deviance:  24.40  on 77  degrees of freedom
AIC: 30.4

Number of Fisher Scoring iterations: 7

>#画拟合概率曲线图
> p<-predict(lgst,type='response')
> plot(seq(-2,2,length=80),sort(p),col='blue')
>
>#画训练样本数据散点图
>a<-testdata$species=='versicolor'
> x1<-testdata[a,'sw']
> y1<-testdata[a,'pw']
> x2<-testdata[!a,'sw']
> y2<-testdata[!a,'pw']
> summary(testdata$sw)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  2.000   2.700   2.900   2.881   3.100   3.800
> summary(testdata$pw)
   Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
  1.000   1.300   1.600   1.672   2.000   2.500
>
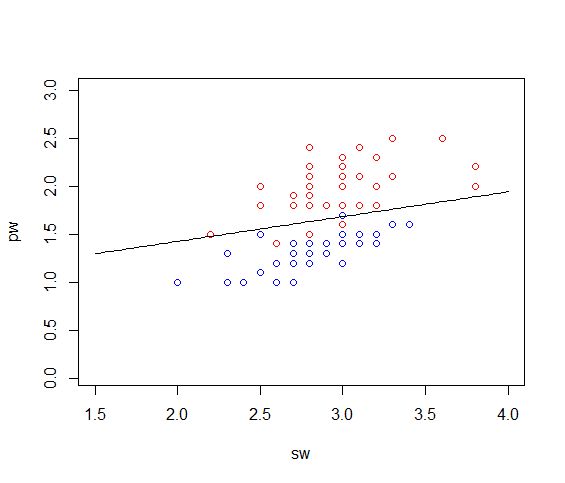
> plot(x1,y1,xlim=c(1.5,4),ylim=c(.05,3),xlab='sw',ylab='pw',col='blue')
> points(x2,y2,col='red')
>
> #画分类边界图，即画h(x)=0.5的图像
> x3<-seq(1.5,4,length=100)
> y3<-(3.796/14.735)*x3+13.415/14.735
> lines(x3,y3)

　　

拟合概率曲线图：

（基本上符合logistic模型的S型曲线）

训练样本散点图及分类边界：

（画logistic回归的分类边界即画曲线h(x)=0.5）