UI相关

Runtime

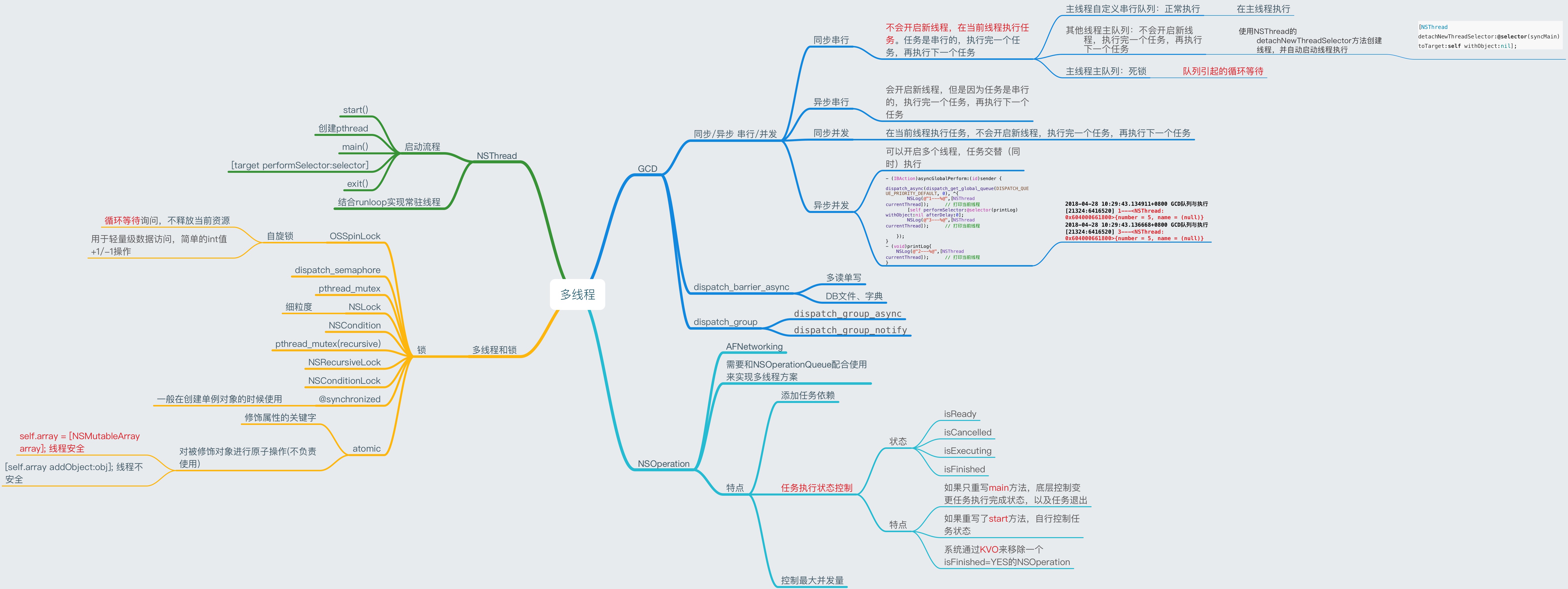
OC特性

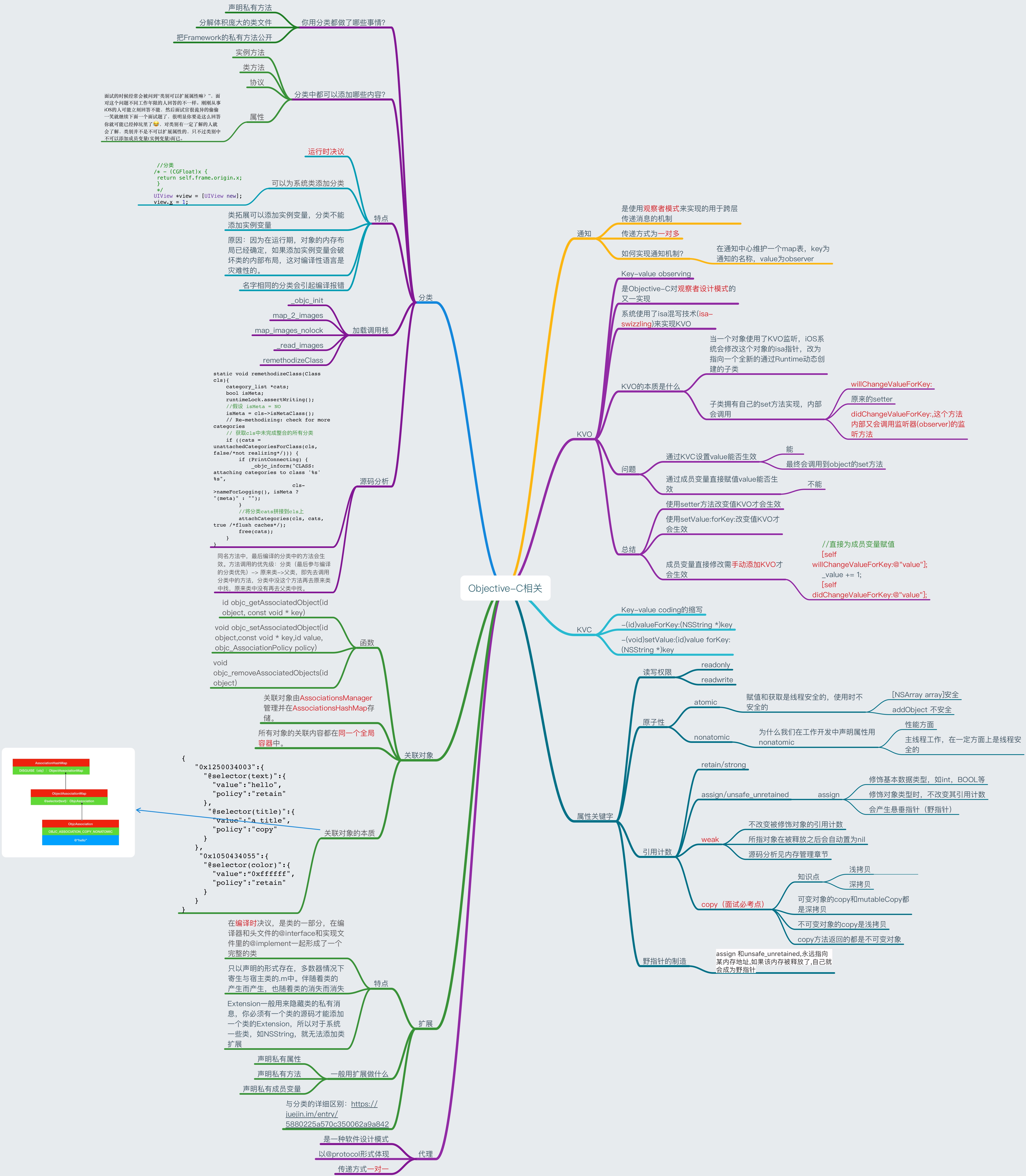
内存管理

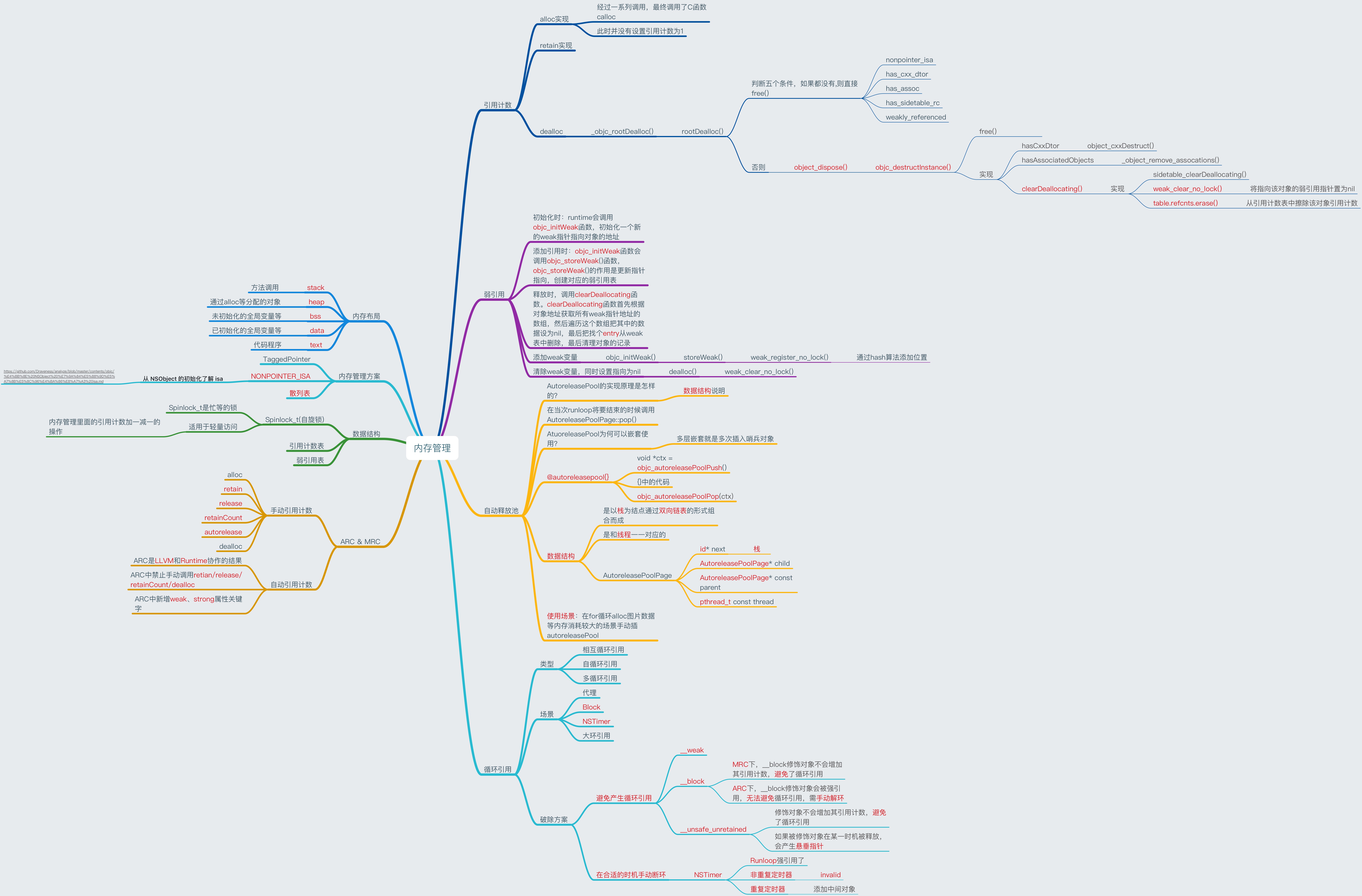
Block

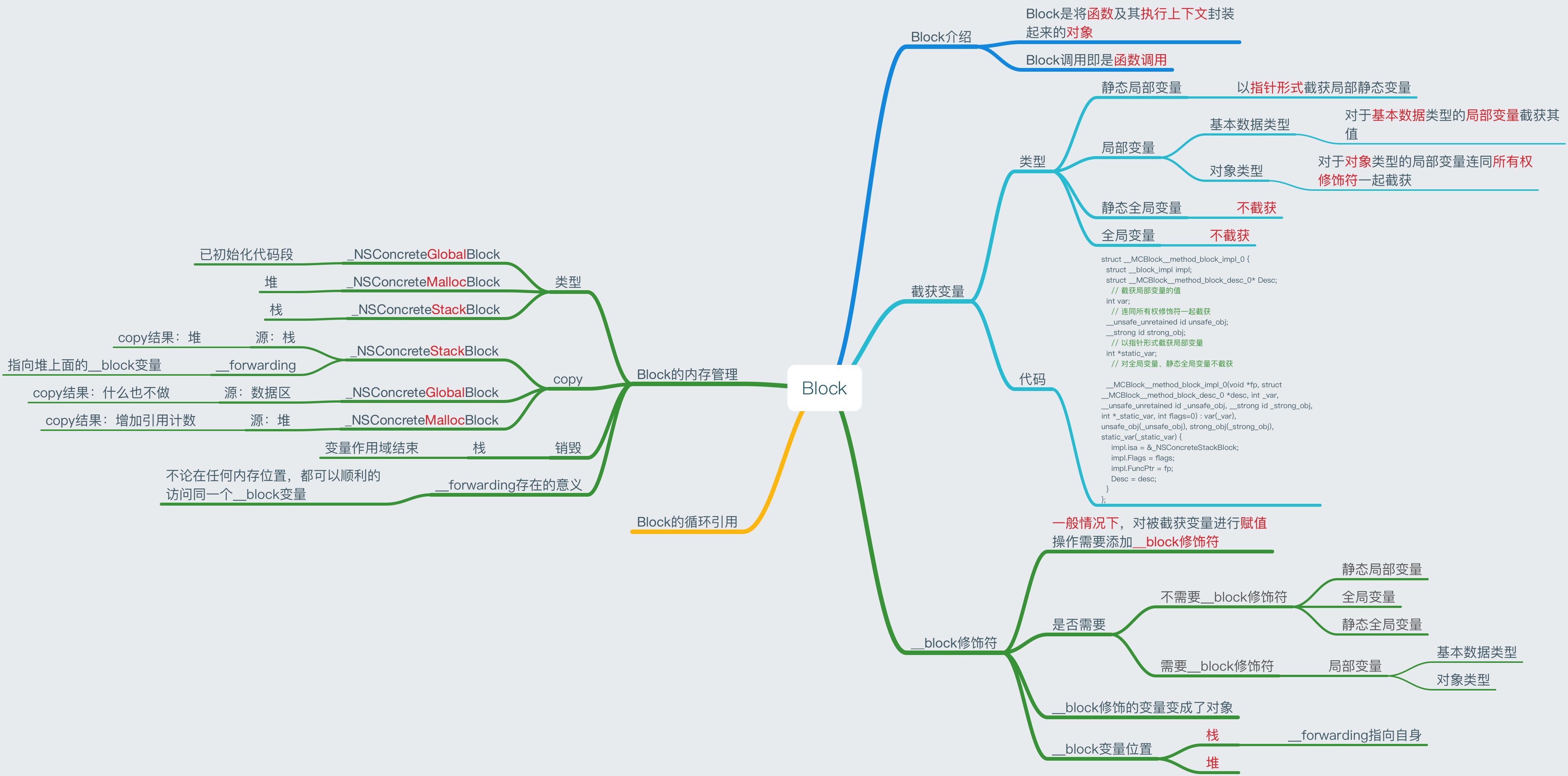
多线程

Runloop

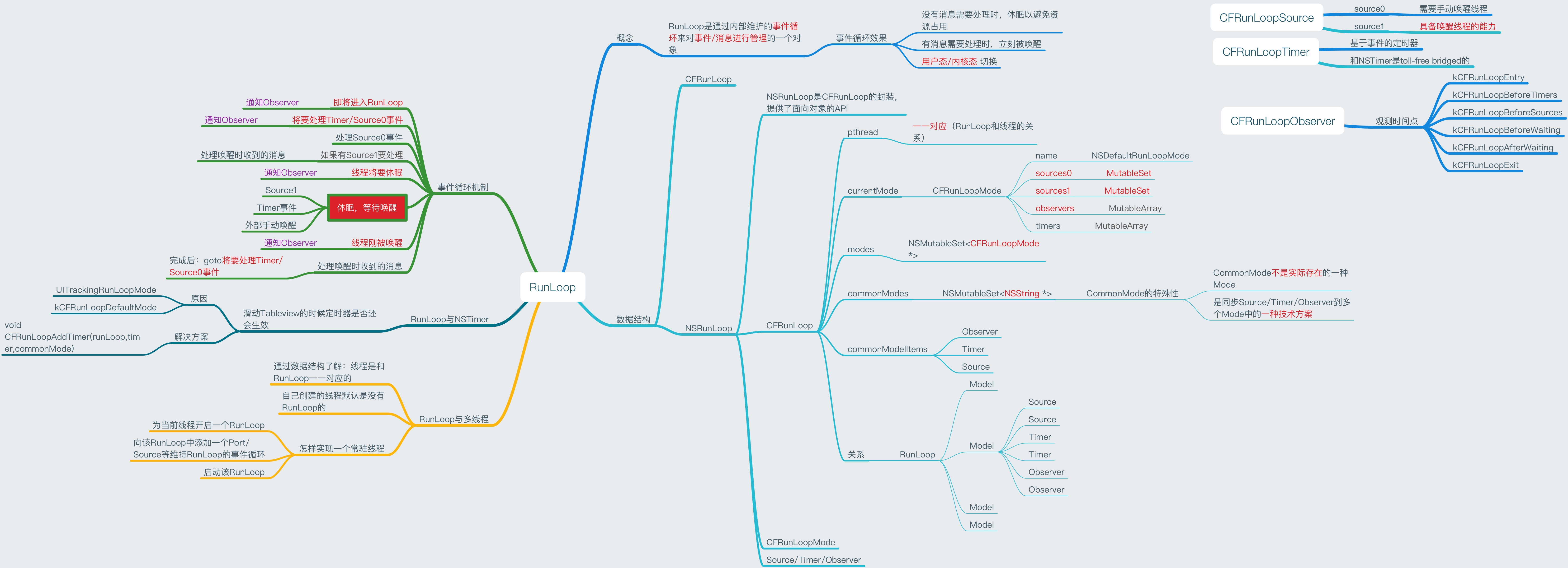
网络相关

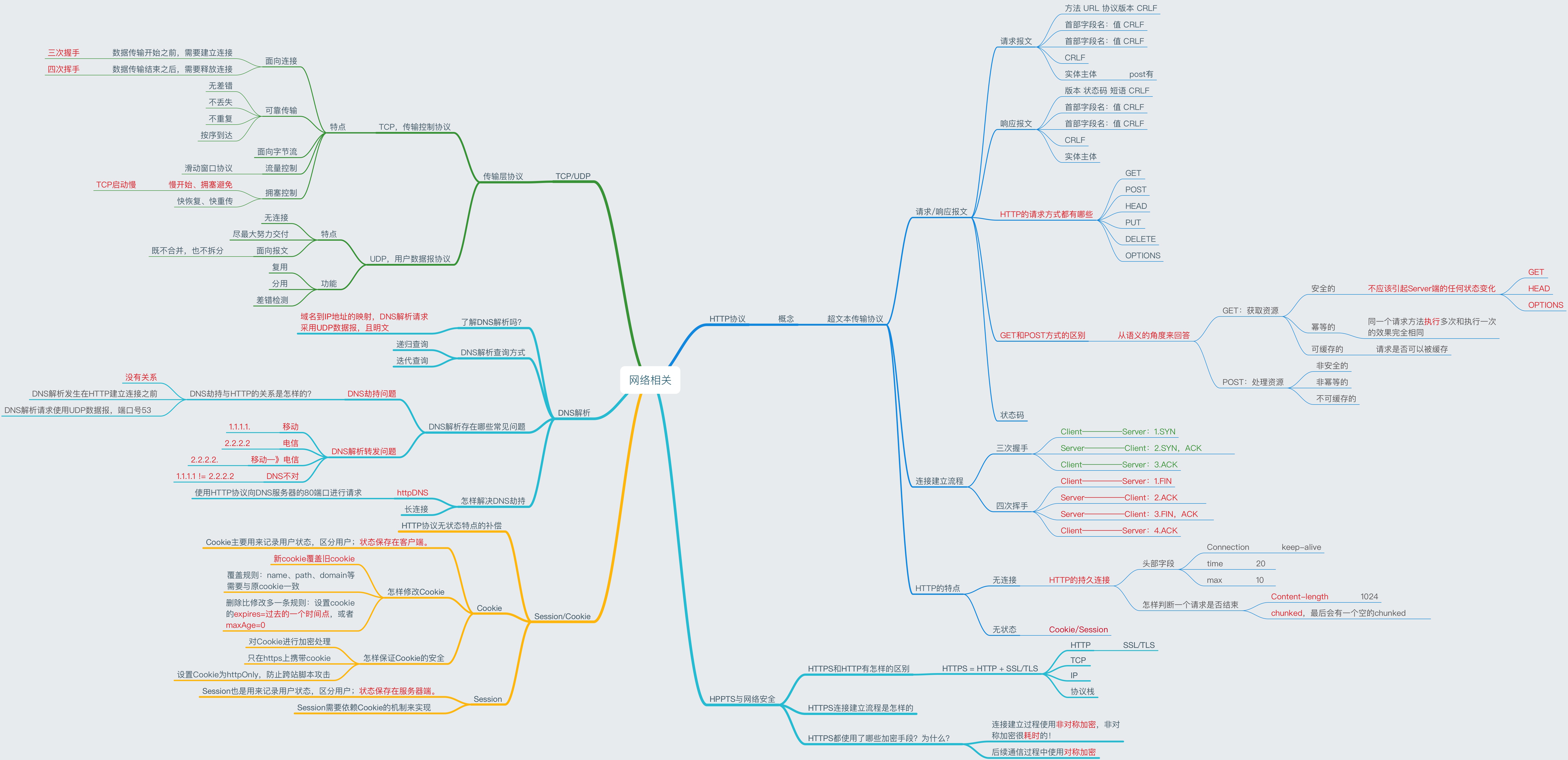
设计模式

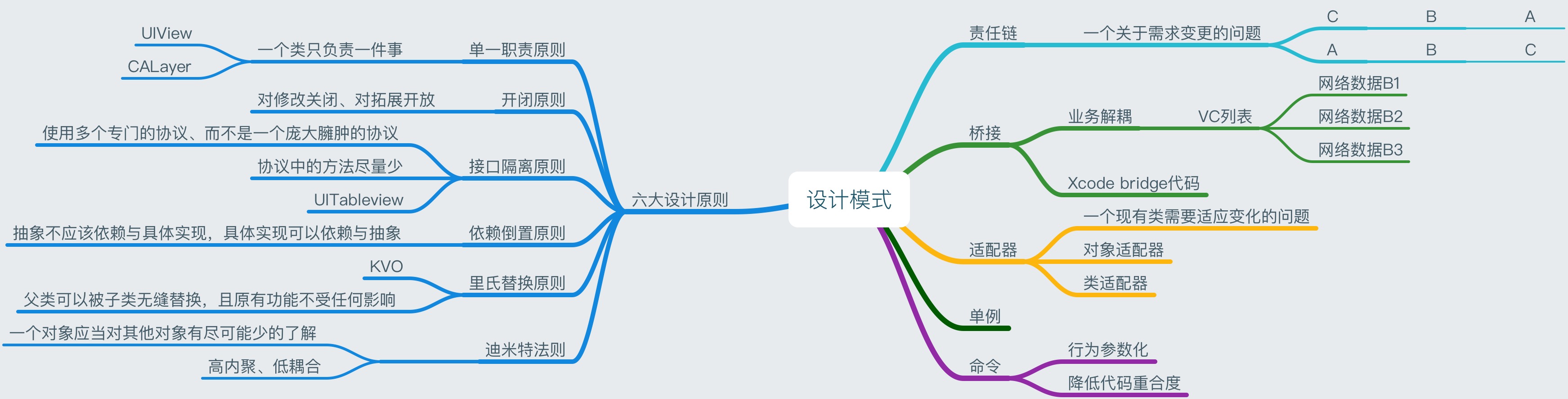
架构

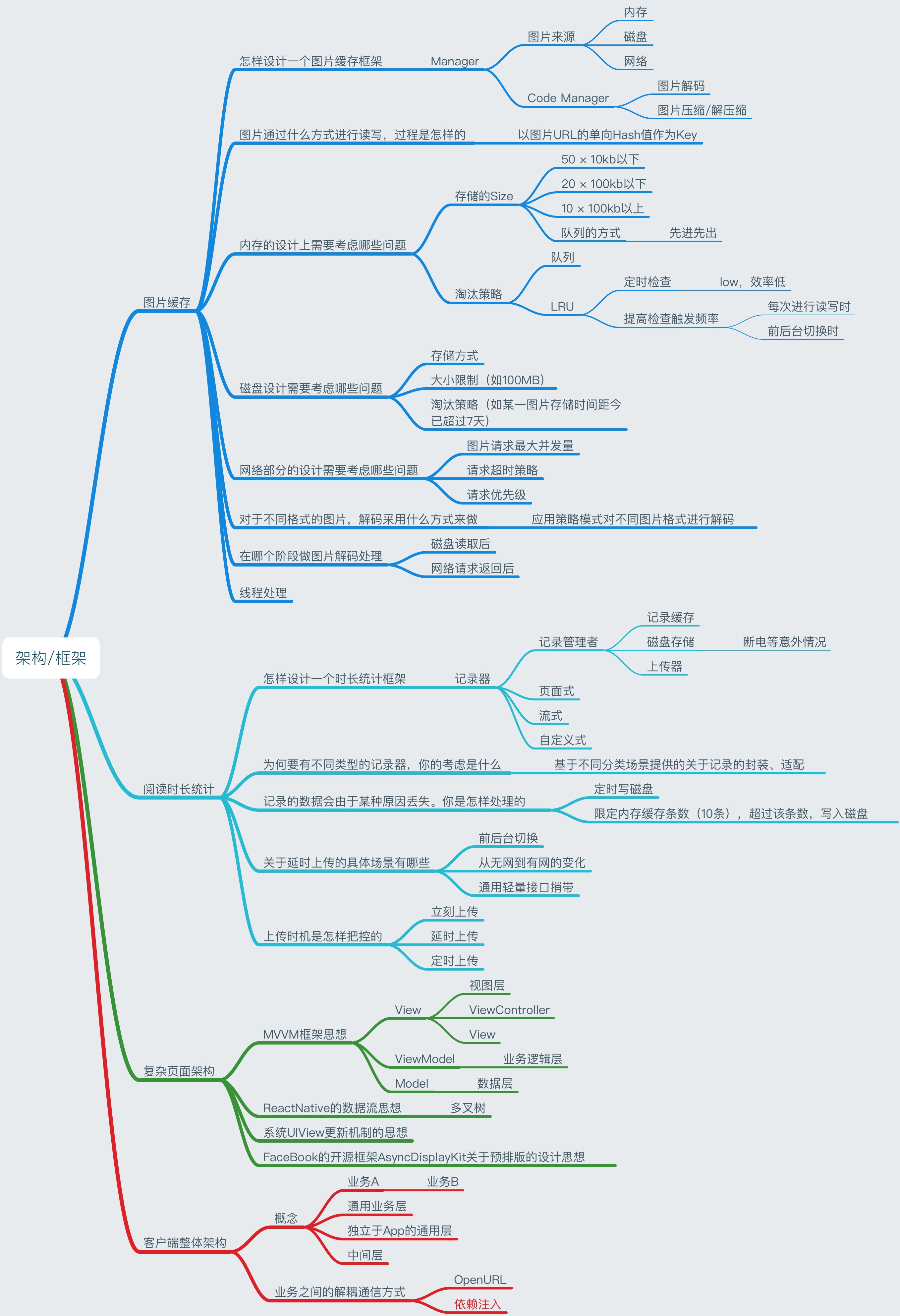
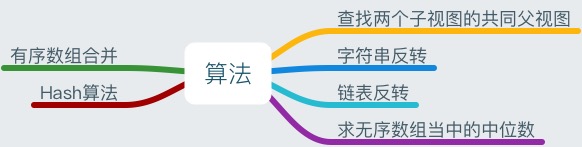
算法

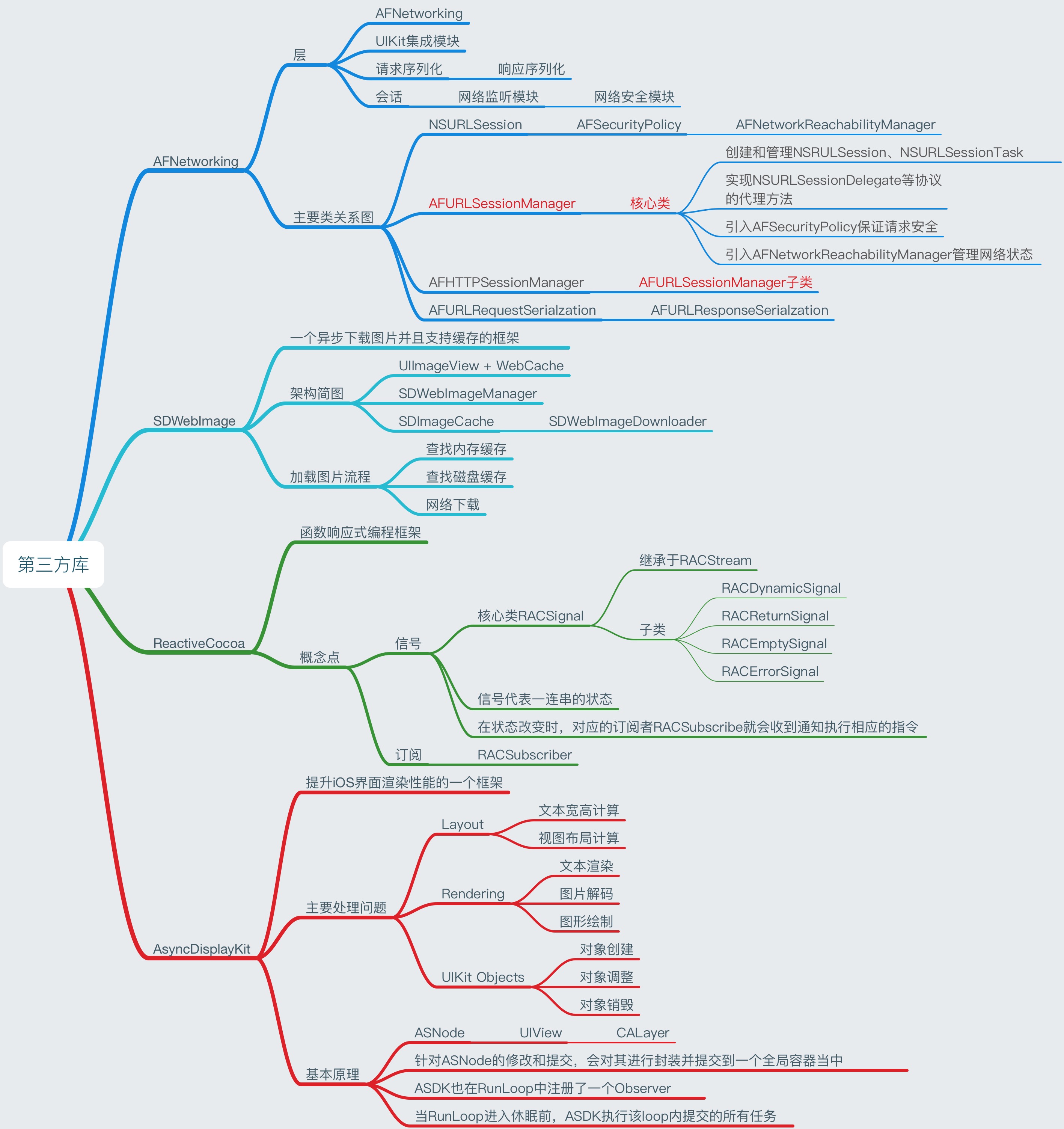
第三方库

iOS----------学习路线思维导图的更多相关文章

  1. Java学习路线思维导图

  2. javascript学习的思维导图

    今天逛师父的博客园,发现了好东西~~~~我给偷过来了~~~那就是javascript学习的思维导图,比自己整理更快速. 思维导图小tips: 思维导图又叫心智图,是表达发射性思维的有效的图形思维工具 ...

  3. C#学习笔记思维导图 一本书22张图

    阅读的书是<21天学通C#>博客中有下载 看看总结之后的模块 全部文件 初步展示 数据存储 继承模块 暂时就这些吧 全部思维导图22张打包下载

  4. LOVO学习之思维导图和文档编辑器

    思维导图——是一种图示笔记方法,一种图示笔记工具,一个思考的利器.能将放射性思考具体化,帮助人们理解和记忆事物. 思维导图绘制规则:1,在纸的正中央用一个彩色图像或者符号开始画思维导图. 2,把所有主 ...

  5. python学习之思维导图

    思维导图——牛刀小试 刚刚学完了python的网络编程,在复习整理知识点的过程中,了解到思维导图是一种强大的工具. 思维导图又叫心智导图,是表达发散性思维的有效图形思维工具 ,它简单却又很有效,是一种 ...

  6. sql server 数据库基础学习心得 思维导图

  7. SQL学习总结-思维导图

  8. Python 学习思路 思维导图 Xmind

    如果需要,请在评论区留下邮箱,我看到后会一次发送.

  9. web前端开发初学者必看的学习路线（附思维导图）

    很多同学想学习WEB前端开发,虽然互联网有很多的教程.网站.书籍,可是却又不知从何开始如何选取.看完网友高等游民白乌鸦无私分享的原标题为<写给同事的前端学习路线>这篇文章,相信你会有所收获 ...

随机推荐

  1. Centos下安装Python的问题汇总

    Python下载地址(https://www.python.org/ftp/python/) 一.工具安装 1.Python的安装 tar vxf Python-2.7.13.tgz cd Pytho ...

  2. PAT1040:Longest Symmetric String

    1040. Longest Symmetric String (25) 时间限制 400 ms 内存限制 65536 kB 代码长度限制 16000 B 判题程序 Standard 作者 CHEN, ...

  3. 3.python元类编程

     1.1.propety动态属性 在面向对象编程中,我们一般把名词性的东西映射成属性,动词性的东西映射成方法.在python中他们对应的分别是属性self.xxx和类方法.但有时我们需要的属性需要根据 ...

  4. SSM-Spring-14：Spring中默认自动代理DefaultAdvisorAutoProxyCreator

    ------------吾亦无他,唯手熟尔,谦卑若愚,好学若饥------------- 默认自动代理DefaultAdvisorAutoProxyCreator 本处没有什么要讲的,放原代码 ISo ...

  5. Java公开课-05.log4j

    log4j 一,log4j简介 1.如果程序中出现异常,我们怎么解决? 01.使用异常处理机制===>异常 (但是使用原则是,能不用异常处理机制,最好不用,怎么办?) 02.通过debug调试 ...

  6. ZooKeeper的使用---命令端

    一.进入命令行 ./bin/zkCli.sh   二.常用命令   命令  作用 范例 备注 connect host:port 连接其他zookeeper客户端 connect hadoop2:21 ...

  7. Mabits简单应用 2017.8.3

    http://www.cnblogs.com/wushiqi54719880/archive/2011/07/26/2117601.html

  8. Java 开发， volatile 你必须了解一下

    上一篇文章说了 CAS 原理,其中说到了 Atomic* 类,他们实现原子操作的机制就依靠了 volatile 的内存可见性特性.如果还不了解 CAS 和 Atomic*,建议看一下我们说的 CAS ...

  9. 关于crontab命令

    crontab命令 crontab命令常见于Unix和类Unix的操作系统之中,用于设置周期性被执行的指令.该命令从标准输入设备读取指令,并将其存放于"crontab"文件中,以供 ...

  10. search_request.go

    package types type SearchRequest struct {     // 搜索的短语(必须是UTF-8格式),会被分词     // 当值为空字符串时关键词会从下面的Token ...