数据库原理剖析 - 序列1

本文节选自《软件架构设计：大型网站技术架构与业务架构融合之道》第6.3章节。
作者微信公众号：架构之道与术。进入后，可以加入书友群，与作者和其他读者进行深入讨论。也可以在京东、天猫上购买纸质书。

关系型数据库在查询方面有一些重要特性，是KV型的数据库或者缓存所不具备的，比如：
（1）范围查询。
（2）前缀匹配模糊查询。
（3）排序和分页。
这些特性的支持，要归功于B+树这种数据结构。下面来分析B+树是如何支持这些查询特性的。

6.3.1 B+树逻辑结构

图6-1展示了数据库的主键对应的B+树的逻辑结构，这个结构有几个关键特征：
（1）在叶子节点一层，所有记录的主键按照从小到大的顺序排列，并且形成了一个双向链表。叶子节点的每一个Key指向一条记录。
（2）非叶子节点取的是叶子节点里面Key的最小值。这意味着所有非叶子节点的Key都是冗余的叶子节点。同一层的非叶子节点也互相串联，形成了一个双向链表。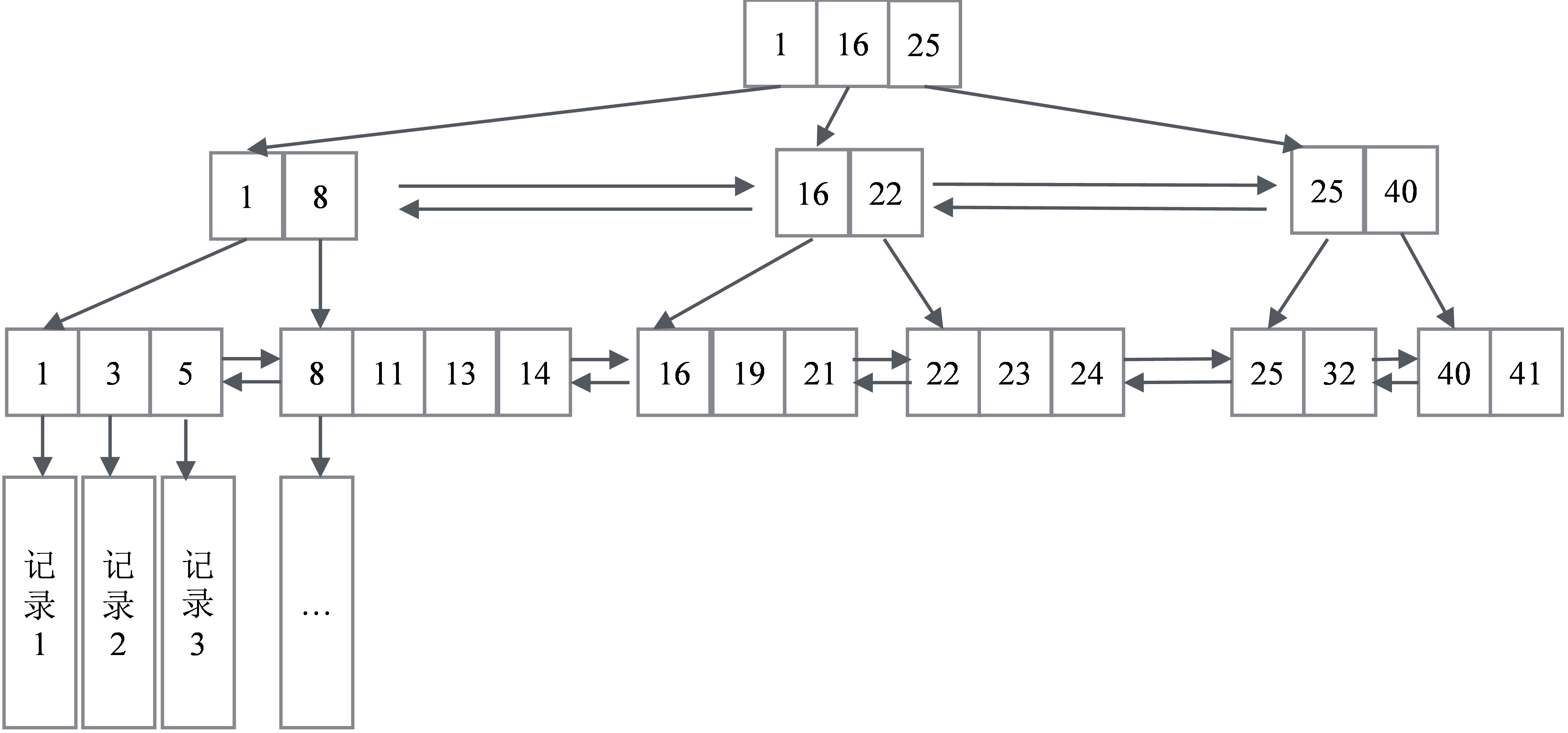

图6-1 数据库的主键对应的B+树的逻辑结构

基于这样一个数据结构，要实现上面的几个特性就很容易了：
 （1）范围查询：比如要查主键在[1,17]之间的记录。二次查询，先查找1所在的叶子节点的记录位置，再查找17所在的叶子节点记录的位置（就是16所处的位置），然后顺序地从1遍历链表直到16所在的位置。
 （2）前缀匹配模糊查询。假设主键是一个字符串类型，要查询where Key like abc%，其实可以转化成一个范围查询Key in [abc,abcz]。当然，如果是后缀匹配模糊查询，或者诸如where Key like %abc%这样的中间匹配，则没有办法转化成范围查询，只能挨个遍历。
 （3）排序与分页。叶子节点天然是排序好的，支持排序和分页。

另外，基于B+树的特性，会发现对于offset这种特性，其实是用不到索引的。比如每页显示10条数据，要展示第101页，通常会写成select xxx where xxx limit 1000, 10，从offset = 1000的位置开始取10条。
虽然只取了10条数据，但实际上数据库要把前面的1000条数据都遍历才能知道offset = 1000的位置在哪。对于这种情况，合理的办法是不要用offset，而是把offset = 1000的位置换算成某个max_id，然后用where语句实现，就变成了select xxx where xxx and id > max_id limit 10，这样就可以利用B+树的特性，快速定位到max_id所在的位置，即是offset=1000所在的位置。

6.3.2 B+树物理结构

上面的树只是一个逻辑结构，最终要存储到磁盘上。下面就以MySQL中最常用的InnoDB引擎为例，看一下如何实现B+树的存储。
对于磁盘来说，不可能一条条地读写，而都是以“块”为单位进行读写的。InnoDB默认定义的块大小是16KB，通过innodb_page_size参数指定。这里所说的“块”，是一个逻辑单位，而不是指磁盘扇区的物理块。块是InnoDB读写磁盘的基本单位，InnoDB每一次磁盘I/O，读取的都是16KB的整数倍的数据。无论叶子节点，还是非叶子节点，都会装在Page里。InnoDB为每个Page赋予一个全局的32位的编号，所以InnoDB的存储容量的上限是64TB（2316KB）。

16KB是一个什么概念呢？如果用来装非叶子节点，一个Page大概可以装1000个Key（16K，假设Key是64位整数，8个字节，再加上各种其他字段），意味着B+树有1000个分叉；如果用来装叶子节点，一个Page大概可以装200条记录（记录和索引放在一起存储，假设一条记录大概100个字节）。基于这种估算，一个三层的B+树可以存储多少数据量呢？如图6-2所示。
第一层：一个节点是一个Page，里面存放了1000个Key，对应1000个分叉。
第二层：1000个节点，1000个Page，每个Page里面装1000个Key。
第三层：10001000个节点（Page），每个Page里面装200条记录，即是10001000200 = 2亿条记录，总容量是16KB10001000，约16GB。
把第一层和第二层的索引全装入内存里，即（1+1000）16KB，也即约16MB的内存。三层B+树就可以支撑2亿条记录，并且一次基于主键的等值查询，只需要一次I/O（读取叶子节点）。由此可见B+树的强大！
基于Page，最终整个B+树的物理存储类似图6-3所示。
Page与Page之间组成双向链表，每一个Page头部有两个关键字段：前一个Page的编号，后一个Page的编号。Page里面存储一条条的记录，记录之间用单向链表串联，最终所有的记录形成图6-1所示的双向链表的逻辑结构。对于记录来说，定位到了Page，也就定位到了Page里面的记录。因为Page会一次性读入内存，同一个Page里面的记录可以在内存中顺序查找。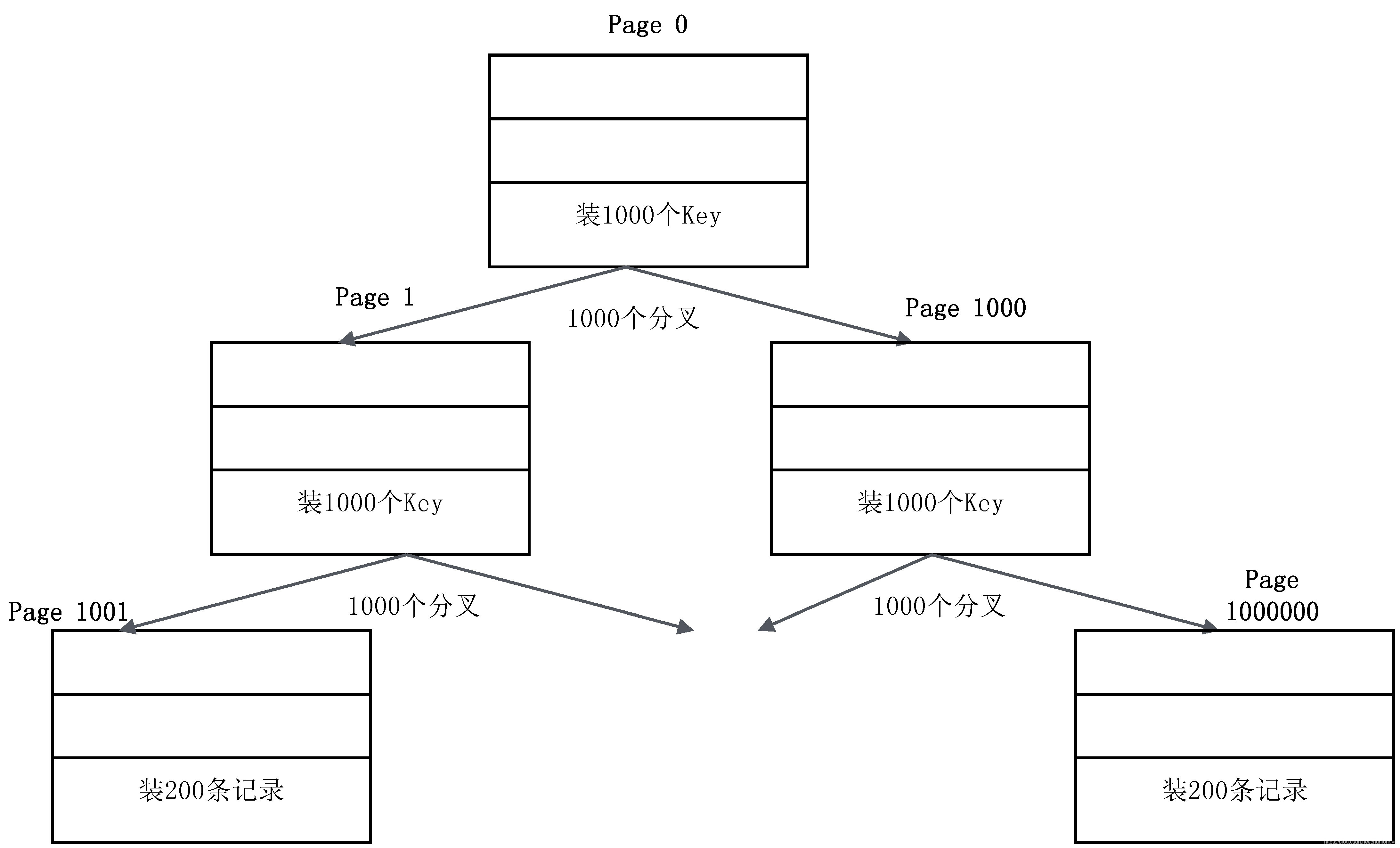

图6-2 三层的磁盘B+树示意图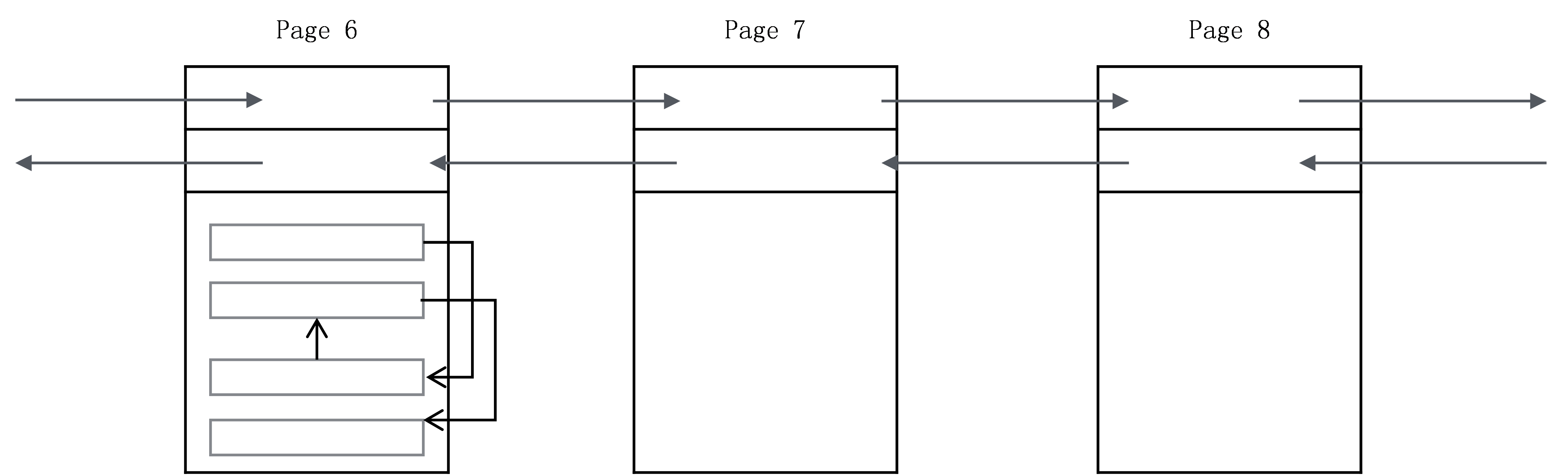

图6-3 B+树物理存储示意图

在InnoDB的实践里面，其中一个建议是按主键的自增顺序插入记录，就是为了避免Page Split问题。比如一个Page里依次装入了Key为（1，3，5，9）四条记录，并且假设这个Page满了。接下来如果插入一个Key = 4的记录，就不得不建一个新的Page，同时把（1，3，5，9）分成两半，前一半（1，3，4）还在旧的Page中，后一半（5，9）拷贝到新的Page里，并且要调整Page前后的双向链表的指针关系，这显然会影响插入速度。但如果插入的是Key = 10的记录，就不需要做Page Split，只需要建一个新的Page，把Key = 10的记录放进去，然后让整个链表的最后一个Page指向这个新的Page即可。
另外一个点，如果只是插入而不硬删除记录（只是软删除），也会避免某个Page的记录数减少进而发生相邻的Page合并的问题。

6.3.3 非主键索引

对于非主键索引，同上面类似的结构，每一个非主键索引对应一颗B+树。在InnoDB中，非主键索引的叶子节点存储的不是记录的指针，而是主键的值。所以，对于非主键索引的查询，会查询两棵B+树，先在非主键索引的B+树上定位主键，再用主键去主键索引的B+树上找到最终记录。
有一点需要特别说明：对于主键索引，一个Key只会对应一条记录；但对于非主键索引，值可以重复。所以一个Key可能对应多条记录，如表6-2所示。假设对于字段1建立索引（字段1是一个字符类型），一个A会对应1，5，7三条记录，C对应8、12两条记录。这反映在B+树的数据结构上面就是其叶子节点、非叶子节点的存储结构，会和主键索引的存储结构稍有不同。
表6-2 非主键索引字段值重复

如图6-4所示，首先，每个叶子节点存储了主键的值；对于非叶子节点，不仅存储了索引字段的值，同时也存储了对应的主键的最小值。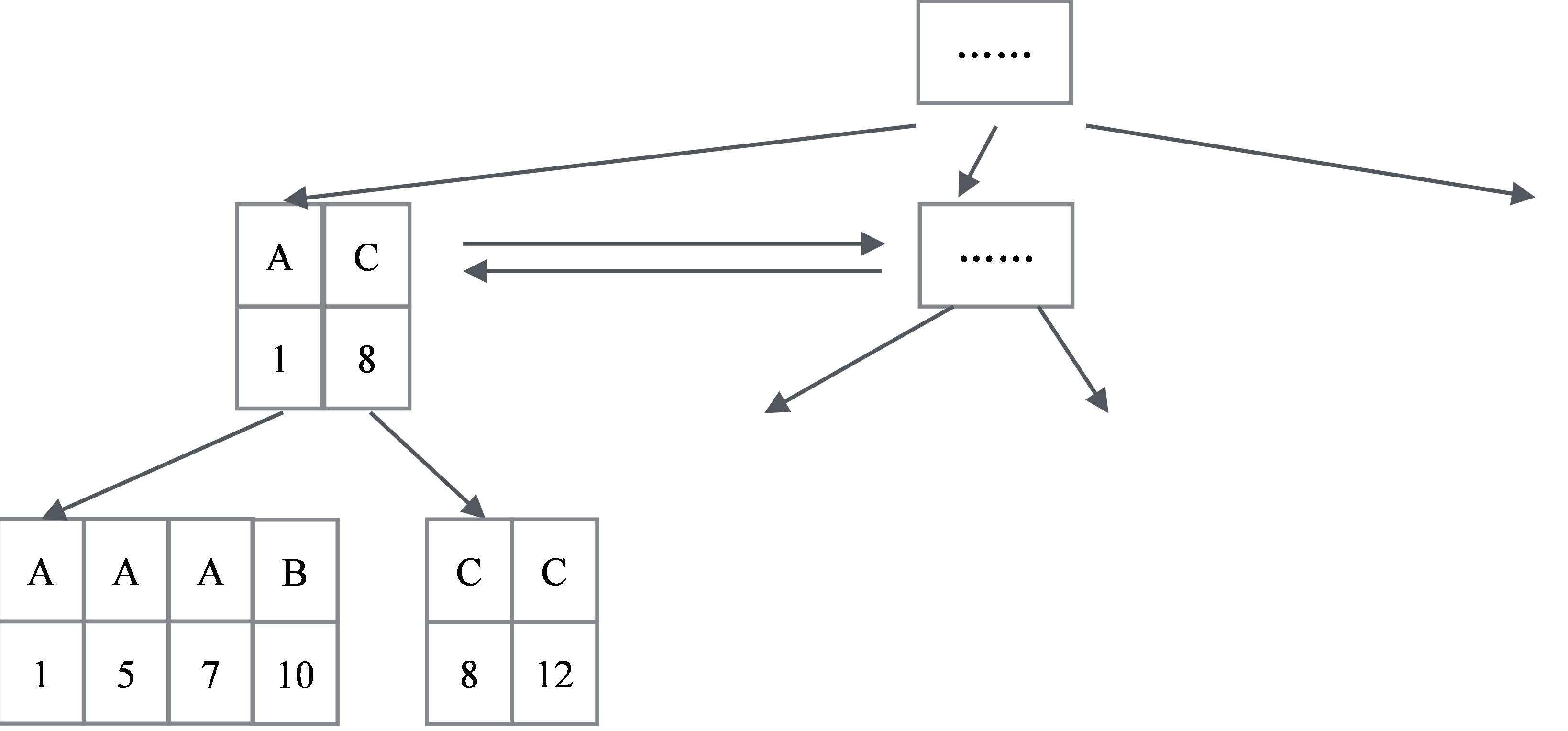

图6-4 非主键索引B+树示意图