Coursera-AndrewNg(吴恩达)机器学习笔记——第三周

一.逻辑回归问题（分类问题）

1. 生活中存在着许多分类问题，如判断邮件是否为垃圾邮件；判断肿瘤是恶性还是良性等。机器学习中逻辑回归便是解决分类问题的一种方法。
   二分类：通常表示为yϵ{0,1}，0：“Negative Class”，1：“Possitive Class”。
2. 逻辑回归的预测函数表达式h_θ(x)（h_θ(x)>=0 && h_θ(x)<=1）：
   

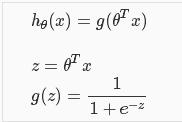
   其中g(z)被称为逻辑函数或者Sigmiod函数，其函数图形如下：
   

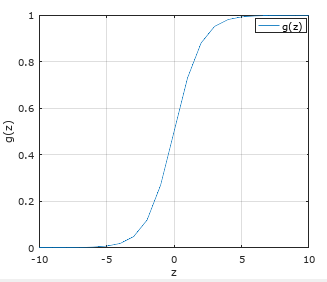
   理解预测函数h_θ(x)的意义：其实函数h_θ(x)的值是系统认为样本值Y为1的概率大小，可表示为h_θ(x)=P(y=1|x;θ)=1-P(y=0|x;θ).

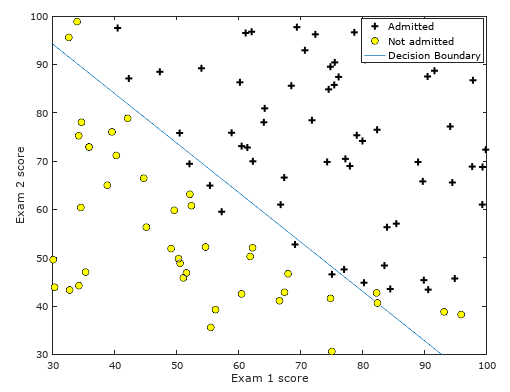
3. 决策边界（Decision boundary）：y=0和y=1的分界线，由逻辑函数图形可知，当y=1时，g(z)>=0.5，z>=0，也就是说θ^TX>=0，这样我们就可以通过以x_i为坐标轴，作出θ^TX=0这条直线，这条直线便是决策边界。如下图所示：
   

4. 代价函数（Cost Function）J(θ)：一定要是一个凸函数（Convex Function），这样经过梯度下降方便找到全局最优 。
   
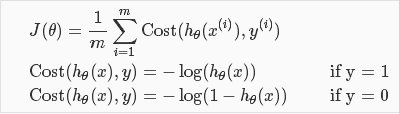
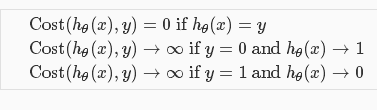
   根据以上两幅图我们可以看出，当预测值h_θ(x)和实际值结果y相同时，代价值为0；当预测值h_θ(x)和实际结果y不同时，代价值无穷大。组合在一起可以写为：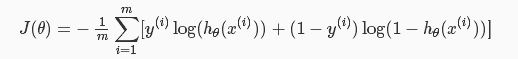
   
   向量化后可写为：
   

5. 梯度下降算法：和线性回归中使用的一样
   
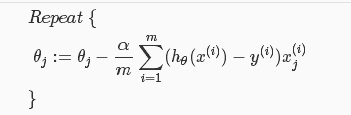
   向量化：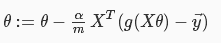
   
6. 高级优化方法（用来代替梯度下降选择参数θ）：Conjugate gradient（共轭梯度法）、BFGS、L-BFGS，只需要掌握用法即可，不需了解原理。
   优点：不需要手动选择学习速率α，收敛速度比梯度下降快，更复杂。

   %首先写一个函数用来计算代价函数和代价函数的梯度
   function [jVal, gradient] = costFunction(theta)
     jVal = [...code to compute J(theta)...];
     gradient = [...code to compute derivative of J(theta)...];
   end
   
   %然后在命令行中通过调用fminunc()函数来计算参数θ

   options = optimset('GradObj', 'on', 'MaxIter', 100);
   initialTheta = zeros(2,1);
   [optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

7. 多分类问题：可以转化为n+1个二分类问题看待，如下：
   

   通过这种形式，我们可以预测出结果最接近哪个y值。

二.过拟合问题和解决方法

1. Underfit：欠拟合问题具有高偏差；Overfit：过拟合问题具有高方差。

2. 过拟合的定义：如果训练集中有过多的特征项，训练函数过于复杂，而训练数据又非常少。我们学到的算法可能会完美的适应训练集，也就是说代价会接近与0。但是却没有对新样本的泛化能力。

3. 解决方法：手动的选择合适的特征；或者使用模型选择算法（用来选取特征变量）。

4. 正规化（Regularization）：正则化中我们将保留所有的特征变量，但是会减小特征变量的数量级（参数数值的大小θ(j)），相当于减少参数θ(j)所对应的多项式对整个预测函数的影响。以下内容以线性回归为例。
   正规化代价函数：其中λ过大会导致欠拟合。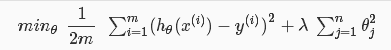
   

   正规化梯度下降：θ₀不需要

   

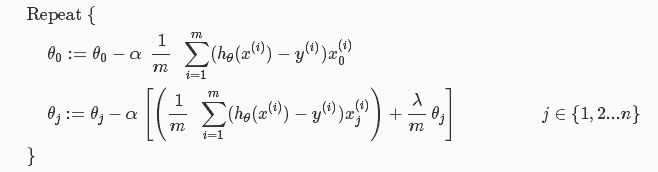
   其中当参数Θ不为θ₀时，梯度下降形式又可以改写为：
   

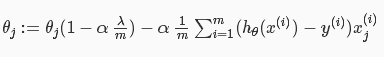
   正规化正规方程：其中L为(n+1)*(n+1)维矩阵。
   

5. 正规化逻辑回归：

   代价函数：
   

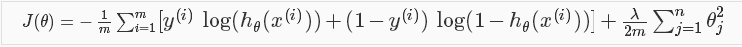
   梯度下降形式和线性回归相同。

6. 正规化逻辑回归中高级的求解参数θ方法：
    
   
   

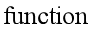
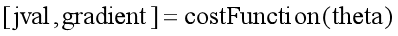
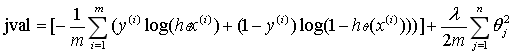
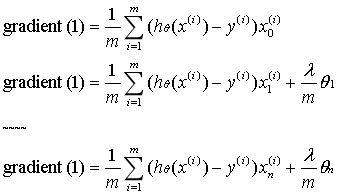
   无~~~~