[LeetCode] Pascal's Triangle II 杨辉三角之二
Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal's triangle.
Note that the row index starts from 0.

In Pascal's triangle, each number is the sum of the two numbers directly above it.
Example:
Input: 3
Output: [1,3,3,1]
Follow up:
Could you optimize your algorithm to use only O(k) extra space?
杨辉三角想必大家并不陌生,应该最早出现在初高中的数学中,其实就是二项式系数的一种写法。
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
杨辉三角形第n层(顶层称第0层,第1行,第n层即第 n+1 行,此处n为包含0在内的自然数)正好对应于二项式 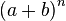 展开的系数。例如第二层 1 2 1 是幂指数为2的二项式
展开的系数。例如第二层 1 2 1 是幂指数为2的二项式 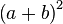 展开形式
展开形式 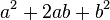 的系数。
的系数。
杨辉三角主要有下列五条性质:
- 杨辉三角以正整数构成,数字左右对称,每行由1开始逐渐变大,然后变小,回到1。
- 第
 行的数字个数为
行的数字个数为 个。
个。 - 第
 行的第
行的第 个数字为组合数
个数字为组合数 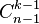 。
。 - 第
 行数字和为
行数字和为 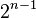 。
。 - 除每行最左侧与最右侧的数字以外,每个数字等于它的左上方与右上方两个数字之和(也就是说,第
 行第
行第 个数字等于第
个数字等于第  行的第
行的第  个数字与第
个数字与第 个数字的和)。这是因为有组合恒等式:
个数字的和)。这是因为有组合恒等式: 。可用此性质写出整个杨辉三角形。
。可用此性质写出整个杨辉三角形。
由于题目有额外限制条件,程序只能使用 O(k) 的额外空间,那么这样就不能把每行都算出来,而是要用其他的方法, 我最先考虑用的是第三条性质,算出每个组合数来生成第n行系数,代码请参见评论区一楼。本地调试输出前十行,没啥问题,拿到 OJ 上测试,程序在第 18 行跪了,中间有个系数不正确。那么问题出在哪了呢,仔细找找,原来出在计算组合数那里,由于算组合数时需要算连乘,而整型数 int 的数值范围只有 -32768 到 32768 之间,那么一旦n值过大,连乘肯定无法计算。而丧心病狂的 OJ 肯定会测试到成百上千行,所以这个方法不行。那么我们再来考虑利用第五条性质,除了第一个和最后一个数字之外,其他的数字都是上一行左右两个值之和。那么我们只需要两个 for 循环,除了第一个数为1之外,后面的数都是上一次循环的数值加上它前面位置的数值之和,不停地更新每一个位置的值,便可以得到第n行的数字,具体实现代码如下:
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<int> res(rowIndex + );
res[] = ;
for (int i = ; i <= rowIndex; ++i) {
for (int j = i; j >= ; --j) {
res[j] += res[j - ];
}
}
return res;
}
};
Github 同步地址:
https://github.com/grandyang/leetcode/issues/119
类似题目:
参考资料:
https://leetcode.com/problems/pascals-triangle-ii/
https://leetcode.com/problems/pascals-triangle-ii/discuss/38420/Here-is-my-brief-O(k)-solution
LeetCode All in One 题目讲解汇总(持续更新中...)
[LeetCode] Pascal's Triangle II 杨辉三角之二的更多相关文章
- [LeetCode] 119. Pascal's Triangle II 杨辉三角之二
Given a non-negative index k where k ≤ 33, return the kth index row of the Pascal's triangle. Note t ...
- [LeetCode] 119. Pascal's Triangle II 杨辉三角 II
Given an index k, return the kth row of the Pascal's triangle. For example, given k = 3,Return [1,3, ...
- Leetcode#118. Pascal's Triangle(杨辉三角)
题目描述 给定一个非负整数 numRows,生成杨辉三角的前 numRows 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 5 输出: [ [1], [1,1], [1,2, ...
- LeetCode 118. Pascal's Triangle (杨辉三角)
Given numRows, generate the first numRows of Pascal's triangle. For example, given numRows = 5,Retur ...
- 每天一道LeetCode--118. Pascal's Triangle(杨辉三角)
Given numRows, generate the first numRows of Pascal's triangle. For example, given numRows = 5,Retur ...
- LeetCode Pascal's Triangle II (杨辉三角)
题意:给出杨辉三角的层数k,返回最后一层.k=0时就是只有一个数字1. 思路:滚动数组计算前一半出来,返回时再复制另一半.简单但是每一句都挺长的. 0ms的版本: class Solution { p ...
- LeetCode(119):杨辉三角 II
Easy! 题目描述: 给定一个非负索引 k,其中 k ≤ 33,返回杨辉三角的第 k 行. 在杨辉三角中,每个数是它左上方和右上方的数的和. 示例: 输入: 3 输出: [1,3,3,1] 进阶: ...
- LeetCode: Pascal's Triangle II 解题报告
Pascal's Triangle II Total Accepted: 19384 Total Submissions: 63446 My Submissions Question Solution ...
- 学会从后往前遍历,例 [LeetCode] Pascal's Triangle II,剑指Offer 题4
当我们需要改变数组的值时,如果从前往后遍历,有时会带来很多麻烦,比如需要插入值,导致数组平移,或者新的值覆盖了旧有的值,但旧有的值依然需要被使用.这种情况下,有时仅仅改变一下数组的遍历方向,就会避免这 ...
随机推荐
- 匹夫细说C#:从园友留言到动手实现C#虚函数机制
前言 上一篇文章匹夫通过CIL代码简析了一下C#函数调用的话题.虽然点击进来的童鞋并不如匹夫预料的那么多,但也还是有一些挺有质量的来自园友的回复.这不,就有一个园友提出了这样一个代码,这段代码如果被编 ...
- 提升用户体验的最佳免费 jQuery 表单插件
网页表单是一个老生常谈的话题.出于这样或那样的目的,一些示例中都会包括用户注册,电子商务结算,用户设置甚至联系人表格.而输入栏是非常容易用现代的CSS3技术来应用样式.但是到底什么决定整体用户体验? ...
- 从.NET和Java之争谈IT这个行业
一.有些事情难以回头 开篇我得表名自己的立场:.NET JAVA同时使用者,但更加偏爱.NET.原因很简单 1.NET语言更具开放性,从开源协议和规范可以看出; 2.语言更具优势严谨; 3.开发工具V ...
- MahApps.Metro使用
# MahApps.Metro使用 # ## 下载MahApps.Metro ## PM> Install-Package MahApps.Metro ## MainWindow.xaml中添加 ...
- 在公有云AZURE上部署私有云AZUREPACK以及WEBSITE CLOUD(二)
前言 (二)建立虚拟网络环境,以及域控和DNS服务器 1搭建虚拟网络环境 在Azure上创建虚拟网络.本例选择的是东南亚数据中心.后面在创建虚机的时候,也选择这个数据中心. VNet Name: ...
- discuz模板语法
Discuz! X 模板的解析主要是 ./source/class/class_template.php 文件解析处理的,如果需要深入了解请可以看看这个文件! 模板嵌套语法 将被嵌套模板内容解析为 P ...
- POI读取EXCEL(2007以上)
import java.io.FileInputStream; import java.io.FileNotFoundException; import java.io.InputStream; im ...
- Socket简单使用
客户端代码: import java.io.*; import java.net.*; public class DailyAdviceClient { public void go(){ try{ ...
- (转)配置Log4j(很详细)
来自:http://blog.csdn.net/yttcjj/article/details/37957317 Log4J的配置文件(Configuration File)就是用来设置记录器的级别.存 ...
- bootstrap(关于栅格布局)
栅格系统是通过行(.row)与列(column)的组合一起来创建页面布局的,所以只有列(column)可以作为行(row)的直接子元素,我们所要写的内容可以放在列里(column),不过在行的外层还需 ...
