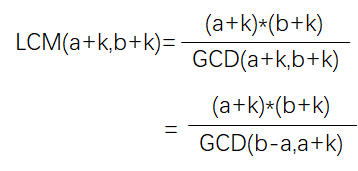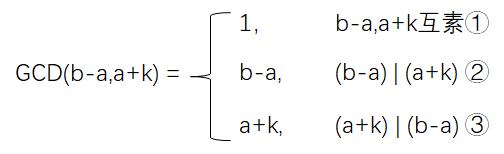Codeforces Round #554 (Div. 2) C. Neko does Maths(数学+GCD)
•题意
给出两个正整数 a,b;
求解 k ,使得 LCM(a+k,b+k) 最小,如果有多个 k 使得 LCM() 最小,输出最小的k;
•思路
刚开始推了好半天公式,一顿xjb乱操作;
后来,看了一下题解,看到一个引理:
GCD(a,b) = GCD(a,b-a) = GCD(b,b-a);
假设GCD(a,b) = c;
a%c = ;
b%c = ;
那么(b-a)%c = ;
这证明了a和(b-a),b和(b-a)有公约数c;
假设GCD(a,b-a)=c' > c;
那么,a%c' = 0;
(b-a)%c' = 0;
(b-a)%c' = b%c'-a%c';
所以 b%c' = 0;
那么GCD(a,b) = c' > c,与假设矛盾;
GCD(b,b-a)同理;
故命题得证;简单证明
有了这个引理后,解题思路变得异常清晰;
首先,令 b > a;
将 LCM(a+k,b+k) 转化一下:
情况①,如果 a 与 b-a 不互素,那么 a+1 与 b-a 一定互素;
情况②,a+k = x·(b-a),其中 x·(b-a) 是大于等于 a 的最小的 (b-a) 的倍数;
情况③,枚举 b-a 的约数;
•Code
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
#define ll long long ll a,b; ll GCD(ll a,ll b)
{
return a == ? b:GCD(b%a,a);
}
ll LCM(ll a,ll b)
{
return a/GCD(a,b)*b;
}
ll F(ll k)
{
return (a+k)*(b+k)/GCD(a+k,b+k);
}
bool isSat(int i,ll k)//判断k是否可以更新为i-a
{
ll curK=i-a;
if(curK < || F(curK) != LCM(a+curK,b+curK))
return false;
if(F(curK) < F(k) || F(curK) == F(k) && curK < k)
return true;
return false;
}
ll Solve()
{
if(a > b)
swap(a,b);
int d=b-a;
if(d == )
return ; ll k=;
for(;GCD(d,a+k) != ;k++);///情况①
for(int i=;i*i <= d;++i)///情况③
{
if(d%i != )
continue;
if(isSat(i,k))///a+k=i
k=i-a;
if(isSat(d/i,k))///a+k=d/i
k=d/i-a;
}
///情况②,GCD()为定值,k越小LCM()就越小
ll x=(a/d+(a%d == ? :))*d;///a+k=k*d(k*d:>=a的最小的d的倍数)
if(isSat(x,k))
k=x-a; return k;
}
int main()
{
scanf("%lld%lld",&a,&b);
printf("%lld\n",Solve()); return ;
}
分割线:2019.7.23
•新想法
GCD(b-a , a+k) = f(b-a);
f(b-a) 表示 b-a 的约数;
当 GCD(b-a,a+k) 确定后,k 越小则 LCM(a+k,b+k) 就越小;
假设 GCD(b-a,a+k) = f;
①如果 a 本身就为 f 的倍数,且 GCD(b-a,a) = f;
那么 k = 0 是满足当前条件下,使得 LCM(a+k,b+k) 最小的最优解;
②反之,如果 a 不为 f 的倍数,那么,找到 ≥ a 的最小的 x·f,并判断 GCD(b-a,x·f) ?= f;
1)如果 GCD(b-a,x·f) = f;
那么 k = x·f-a 是满足当前条件下,使得 LCM(a+k,b+k) 最小的最优解;
2)如果 GCD(b-a,x·f) ≠ f;
那么 GCD(b-a,(x+1)·f)一定等于 f;
GCD(b-a,x·f) = GCD(y·f,x·f) = f·GCD(x,y);
判断 GCD(b-a,x·f) ?= f ⇔ 判断 GCD(y,x) ?= 1;
如果 GCD(y,x) ≠ 1,那么一定有 GCD(y,x+1) = 1;
•Code
#include<bits/stdc++.h>
using namespace std;
#define GCD(a,b) __gcd(a,b)
#define ll long long ll a,b; ll g(ll k)
{
return (a+k)/GCD(a+k,b+k)*(b+k);
}
void update(ll f,ll &k)
{
ll x=a/f+(a%f != );///找到使得x·f ≥ a的最小的x
ll y=(b-a)/f; if(GCD(x,y) != )
x++; ///判断是否更新k
ll cur=x*f-a;
if(k == - || g(k) > g(cur))
k=cur;
else if(g(k) == g(cur))
k=min(k,cur);
}
ll Solve()
{
if(a == b)
return ;
if(b < a)
swap(a,b); ll k=-; for(ll i=;i*i <= b-a;++i)
{
if((b-a)%i != )
continue; update(i,k);
update((b-a)/i,k);
} return k;
}
int main()
{
scanf("%lld%lld",&a,&b);
printf("%lld\n",Solve()); return ;
}
Codeforces Round #554 (Div. 2) C. Neko does Maths(数学+GCD)的更多相关文章
- Codeforces Round #554 (Div. 2) C. Neko does Maths (简单推导)
题目:http://codeforces.com/contest/1152/problem/C 题意:给你a,b, 你可以找任意一个k 算出a+k,b+k的最小公倍数,让最小公倍数尽量小,求出 ...
- Codeforces Round #554 (Div. 2) C.Neko does Maths (gcd的运用)
题目链接:https://codeforces.com/contest/1152/problem/C 题目大意:给定两个正整数a,b,其中(1<=a,b<=1e9),求一个正整数k(0&l ...
- Codeforces Round #554 (Div. 2) C. Neko does Maths (数论 GCD(a,b) = GCD(a,b-a))
传送门 •题意 给出两个正整数 a,b: 求解 k ,使得 LCM(a+k,b+k) 最小,如果有多个 k 使得 LCM() 最小,输出最小的k: •思路 时隔很久,又重新做这个题 温故果然可以知新❤ ...
- Codeforces Round #554 (Div. 2) 1152B. Neko Performs Cat Furrier Transform
学了这么久,来打一次CF看看自己学的怎么样吧 too young too simple 1152B. Neko Performs Cat Furrier Transform 题目链接:"ht ...
- Codeforces Round #554 (Div. 2) 1152A - Neko Finds Grapes
学了这么久,来打一次CF看看自己学的怎么样吧 too young too simple 1152A - Neko Finds Grapes 题目链接:"https://codeforces. ...
- Codeforces Round #554 (Div. 2) B. Neko Performs Cat Furrier Transform(思维题+log2求解二进制位数的小技巧)
传送门 题意: 给出一个数x,有两个操作: ①:x ^= 2k-1; ②:x++; 每次操作都是从①开始,紧接着是② ①②操作循环进行,问经过多少步操作后,x可以变为2p-1的格式? 最多操作40次, ...
- Codeforces Round #554 (Div. 2) E Neko and Flashback (欧拉路径 邻接表实现(当前弧优化..))
就是一欧拉路径 贴出邻接表欧拉路径 CODE #include <bits/stdc++.h> using namespace std; const int MAXN = 100005; ...
- Codeforces Round #554 (Div. 2) F2. Neko Rules the Catniverse (Large Version) (矩阵快速幂 状压DP)
题意 有nnn个点,每个点只能走到编号在[1,min(n+m,1)][1,min(n+m,1)][1,min(n+m,1)]范围内的点.求路径长度恰好为kkk的简单路径(一个点最多走一次)数. 1≤n ...
- Codeforce Round #554 Div.2 C - Neko does Maths
数论 gcd 看到这个题其实知道应该是和(a+k)(b+k)/gcd(a+k,b+k)有关,但是之后推了半天,思路全无. 然而..有一个引理: gcd(a, b) = gcd(a, b - a) = ...
随机推荐
- MySQL中SELECT语句简单使用
最近开始复习mysql,查漏补缺吧. 关于mysql 1.MySQL不区分大小写,但是在MySQL 4.1及之前的版本中,数据库名.表名.列名这些标识符默认是区分大小写的:在之后的版本中默认不区分大小 ...
- vue学习之vuex
1 首先还是安装 npm install vuex --save. 2 在src这种创建目录为store 创建 index.js (getters.js ,actions.js ,mutation ...
- Django 无名参数与有名参数
无名参数 配置 urls ,我们需要导入 url 模块,以()定义一个无名的变量 from django.contrib import admin from django.urls import pa ...
- Kotlin 扩展——省略findViewById
现在 Kotlin 安卓扩展插件能够提供与这些开源库功能相同的体验,不需要添加任何额外代码. import kotlinx.android.synthetic.main.activity_main.* ...
- 【SpringBoot笔记】SpringBoot如何正确关闭应用
关闭Spring Boot应用程序,我们可以通过OS命令kill -9 进程ID 实现将进程杀死.但是,有没有一种更好的方式,比如通过REST请求实现?Spring Boot Actoator提供了实 ...
- Redis 安装总结记录 附送redis-desktop-manager工具
使用redis已几年有余,之前写过Redis关于master-slave(主从)同步原理的文章.这里介绍下安装过程,因为前前后后有些命令也记不住了,所以此篇文章和之前文章一样起个备注记录作用,也供屏幕 ...
- Unity NPOI 无法读取xlsx
遇到问题 在做编辑器开发时,需要在Unity Editor下直接读取Excel源文件,首先想到的是通过npoi去读取,但是遇到无法读取xlsx格式,只能读取xls格式的问题. 我的环境 unity 2 ...
- SQL server 2017使用教程
1.安装: 从https://www.microsoft.com/en-us/sql-server/sql-server-downloads官网下载sql server2017试用版 180天 安装完 ...
- windows10安装mysql-8.0.13(zip安装)
安装环境说明 系统版本:windows10 mysql版本:mysql-8.0.13-winx64.zip 下载地址:http://mirrors.163.com/mysql/Downloads/My ...
- RobotFramework第二篇之web自动化
(1)安装seleniumLibrary库: pip install --upgrade --pre robotframework-seleniumlibrary 使用第三方库关键字: (1)sett ...