[POI2007]对称轴osi

Description

FGD小朋友——一个闻名遐迩的年轻数学家——有一个小MM，yours。FGD小朋友非常喜欢他的MM，所以他很乐意帮助他的MM做数学作业。但是，就像所有科学的容器一样，FGD的大脑拒绝不停地重复思考同样的问题。不幸的是，yours是一个十分用功的学生，所以她不停地让FGD帮助她检查她的作业。一个阳光明媚的周末，yours的数学老师布置了非常多的寻找多边形的对称轴的题，足够她做相当长的一段时间了。在此之前FGD已经决定去海边度过这个难得的假期，不过他还是觉得应该帮助他的MM对付可爱的数学作业。很快地，他找到了解决方案，最好写一个程序来帮助yours检查她的数学作业。因为FGD并非一个计算机科学家，所以他找到了他的好朋友你，请你帮助他完成这个任务。请写一个程序：读入多边形的描述计算出每个多边形的对称轴数将计算的结果输出

Input

输入的第一行包含一个正整数t(1<=t<=10)，为多边形的边数。接下来，为t个多边形的描述，每个描述的第一行为一个正整数n(3<=n<=100000)，表示了多边形的点数。然后在后面n行每行两个整数x和y(?100000000<=x, y<=100000000)，依次表示多边形的顶点坐标。多边形不一定是凸的，但是不自交——任何两条边都只有最多一个公共点——他们的公共端点。此外，没有两条连续的边平行。

Output

你的程序应该输出正好t行，第k行包含了一个整数nk——表示第k个多边形有多少个对称轴。

Sample Input

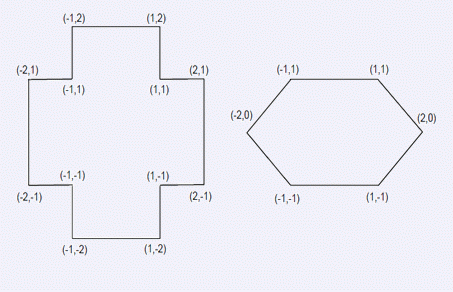
2

12

1 -1

2 -1

2 1

1 1

1 2

-1 2

-1 1

-2 1

-2 -1

-1 -1

-1 -2

1 -2

6

-1 1

-2 0

-1 -1

1 -1

2 0

1 1

Sample Output

4

2

HINT

---

首先这个题目把我吓到了……计算几何毒瘤题，完全不费……

然后看看别人的代码长度，好像又不毒瘤的样子？？？

实在不会的本蒟蒻只好去看看题解，看完之后跪%题解，居然是字符串！

把多边形用类似字符串的形式存下来，然后倍长，跑一遍Manacher即可。答案记得除2，因为对称轴会被算两次

/*program from Wolfycz*/
#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define inf 0x7f7f7f7f
#define sqr(x) ((x)*(x))
using namespace std;
typedef long long ll;
typedef unsigned int ui;
typedef unsigned long long ull;
inline int read(){
	int x=0,f=1;char ch=getchar();
	for (;ch<'0'||ch>'9';ch=getchar())	if (ch=='-')    f=-1;
	for (;ch>='0'&&ch<='9';ch=getchar())	x=(x<<1)+(x<<3)+ch-'0';
	return x*f;
}
inline void print(int x){
	if (x>=10)     print(x/10);
	putchar(x%10+'0');
}
const int N=1e5;
struct S1{int x,y;}A[N+10];
int s[(N<<2)+10],p[(N<<2)+10];
int dis(int x,int y){return sqr(A[x].x-A[y].x)+sqr(A[x].y-A[y].y);}
int cro(int x,int y,int z){return (A[y].x-A[x].x)*(A[z].y-A[x].y)-(A[z].x-A[x].x)*(A[y].y-A[x].y);}
int main(){
	for (int Data=read();Data;Data--){
		int n=read();
		for (int i=0;i<n;i++)	A[i].x=read(),A[i].y=read();
		for (int i=0;i<n;i++)	s[i<<1|1]=dis(i,(i+1)%n);
		for (int i=0;i<n;i++)	s[i<<1]=cro(i,(i-1+n)%n,(i+1)%n);
		for (int i=0;i<n<<1;i++)	s[i+(n<<1)]=s[i];
		int Ans=0,Max=0,ID=0;
		for (int i=0;i<n<<2;i++){
			p[i]=Max>i?min(p[ID*2-i],Max-i):1;
			while (i-p[i]>=0&&i+p[i]<n<<2&&s[i+p[i]]==s[i-p[i]])	p[i]++;
			if (Max<i+p[i])	Max=p[ID=i]+i;
			if (p[i]>n)	Ans++;
		}
		printf("%d\n",Ans>>1);
	}
	return 0;
}