算法导论 第八章 线性时间排序（python）

比较排序：各元素的次序依赖于它们之间的比较{插入排序O(n**2) 归并排序O(nlgn) 堆排序O(nlgn)快速排序O(n**2)平均O(nlgn)}

本章主要介绍几个线性时间排序：（运算排序非比较排序）计数排序O(k+n)基数排序O()

第一节：用决策树分析比较排序的下界

决策树：倒数第二层满，第一层可能满的二叉树，它用来表示所有元素的比较操作{于此来分析下界}，忽略控制，移动操作

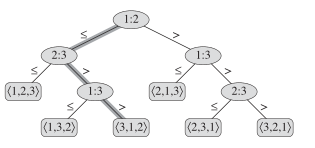
1:2 #A[1]和A[2]比 <= 走左边 >走右边

<3,1,2> 最后的结果 下标对应排序顺序

如A=[5,6,4]-->1:2 <=  -->2:3 > -->1:3 > ---><3,1,2>[4,5,6]

看图可知有6钟可能的对比3!（也就是n!）

高度是他要对比的次数h = Ω(n lg n)

n! <= 2**h#数据结构内容

推出8.2：堆排序和归并排序都是渐进最优的比较排序算法

二计数排序

基本思想：对于每个元素x，确定小于x的元素个数

适用范围：小范围 x的跨度比较小的整数排序#跨度过大如0-1000辅助函数C[1000]

稳定性：稳定

时间复杂度：Θ(k+n)

实现：

def COUNTING_SORT(A,B,k):
    #A要排序的函数
    #B保存排序后的结果
    #k A中x的最大值 [0,k]
 
    C = list() #临时保存记录x前面的个数
    for i in range(k+1):#[0,k]
        C.append(0)
 
    for j in range(len(A)):
        C[A[j]] += 1 #记录A[j] == i C[i]记一个数 这是一个转换 似于hash的思想
 
    for i in range(1,k+1):
        C[i] = C[i] + C[i-1] #计算小于x的元素个数
 
    for j in range(len(A)-1,-1,-1): # 从后想前借B排序[0,len(A))
        #print(C[A[j]])
        B[C[A[j]]-1] = A[j] #B下标从0开始
        C[A[j]] -= 1
 
if __name__ == "__main__":
    A = [2,5,3,0,2,3,0,3]
    B = list()
    for i in range(len(A)): #B初始化？还有没有别的方法
        B.append(0)
    COUNTING_SORT(A,B,5)
    print(B)
 
'''
>>>
============= RESTART: F:/python/algorithms/8_2_counting_sort.py =============
[0, 0, 2, 2, 3, 3, 3, 5]
 
win7 python3.5.1
'''

8.3基数排序（radix sort）

基本思想：按关键字的各个值来排序

排序方式：LSD 由右向左排; MSD 由左向右排

稳定性：稳定

基数：在数学上，基数或势，即集合中包含的元素的“个数”

基数：计算的基数就是基本的单元数。比如10进制的基数就是10，二进制的基数就2，八进制的基数是8等等

基数排序：一位一位的对比排序（msd）

arr = list()
res = list()
hash = list()
n = int()
 
def maxbit():
    _max = 0
    temp = list()
    for i in arr:
        temp.append(i)
 
    for i in range(n):
        tt = 1
        while (temp[i] //10) >0:
            tt += 1
            temp[i] //= 10
        if _max < tt:
            _max = tt
 
    print("最大%d位"%_max)
    return _max
 
def radixSort():
    for i in range(n):
        res.append(0)#初始化为0
    nbit = maxbit() #最大的数有多少位
    radix = 1
    #计数排序
    for j in range(10):
            hash.append(0)
 
    for i in range(1,nbit+1):#[1,3]
        for j in range(10):
            hash[j] = 0
        for j in range(n):
            tmp = (arr[j]//radix) % 10
            hash[tmp] += 1
        for j in range(1,10):
            hash[j] += hash[j-1]
        for j in range(n-1,-1,-1):
            tmp = (arr[j]//radix) %10
            hash[tmp] -= 1
            #print(hash[tmp])
            res[hash[tmp]] = arr[j]
 
        for  j in range(n):
            arr[j] = res[j]
        print(arr)
        radix *= 10;
 
if __name__ == "__main__":
    n = int(input("输入元素个数:"))
    print("输入%d个元素"%n)
    for i in range(n):
        arr.append(int(input("第"+str(i+1)+'个:')))
    radixSort()
    print("排序后",arr)
'''
============== RESTART: F:/python/algorithms/8_3_radix_sort.py ==============
输入元素个数:5
输入5个元素
第1个:54321
第2个:1
第3个:4321
第4个:21
第5个:321
最大5位
[54321, 1, 4321, 21, 321]
[1, 54321, 4321, 21, 321]
[1, 21, 54321, 4321, 321]
[1, 21, 321, 54321, 4321]
[1, 21, 321, 4321, 54321]
排序后 [1, 21, 321, 4321, 54321]
>>> 
 
环境：win7 + python3.5.1
'''

8.4桶排序

思想：同hash = n //x

稳定性：

def bucketSort(a,max):
    #a 待排序list
    #数组中的最大值的范围
    if len(a) == 0 and max <1 :
        return
    buckets = list() #建立容纳max个数的list
    for i in range(max):
        buckets.append(0) #初始化
 
    #计数
    for i in range(len(a)):
        buckets[a[i]] += 1
 
    #排序
    j = 0
    for i in range(max):
        while buckets[i] >0:
            buckets[i] -= 1
            a[j] = i
            j += 1
 
if __name__ == "__main__":
    a = [8,2,3,4,3,6,6,3,9]
    print("排序前a:",a)
    bucketSort(a,10) #桶排序
    print("排序后a:",a)
 
'''
============== RESTART: F:/python/algorithms/8_4_bucket_sort.py ==============
排序前a: [8, 2, 3, 4, 3, 6, 6, 3, 9]
排序后a: [2, 3, 3, 3, 4, 6, 6, 8, 9]
>>> 
 
win7 + python3.5.1
'''

参考引用：

http://www.wutianqi.com/?p=2378

https://zh.wikipedia.org/wiki/%E5%9F%BA%E6%95%B0_(%E6%95%B0%E5%AD%A6)

http://www.cnblogs.com/skywang12345/p/3602737.html#a32