BSGS算法 （小步大步 Baby Step Gaint Step）

当你要求满足：

$$ A^x \equiv B \ (\bmod \ P) $$

的最小非负整数 x （gcd(A,P)==1）就可以用到 BSGS 了

设 $ m=\sqrt{P} $ 向上取整

处理一下那个式子：

$$ A^{i \times m-j} \equiv B \ (\bmod \ P) $$
$$ A^{i \times m} \equiv B \times A^j \ (\bmod \ P) $$

枚举 j（0到m），将 B*A^j 存入hash表里面
枚举 i（1到m），从hash表中找第一个满足上面这条式子的 j
x=i*m-j 即为所求 （感性理解）

模板题： 【xsy 1754】 离散对数

Description

给定B,N,P，求最小的满足B^L=N(mod P)的非负正数L。保证gcd(B,P)=1。

Input

        多组数据，每行三个空格隔开的整数P,B,N。

Output

        对于每组数据，输出答案。如无解，则输出"no solution"

CODE：

 #include<iostream>
 #include<cmath>
 #include<cstdio>
 #include<unordered_map>
 using namespace std;

 int p,a,b;

 int qpow(int x,int y){
     int ans=;
     while(y){
         if(y&)ans=1LL*ans*x%p;
         y>>=,x=1LL*x*x%p;
     }
     return ans;
 }

 int BSGS(){
     unordered_map<int,int> mp;
     int m=ceil(sqrt(p)),tmp;
     tmp=b;
     for(int j=;j<=m;j++)
         mp[tmp]=j,tmp=1LL*tmp*a%p;
     tmp=a=qpow(a,m);
     for(int i=;i<=m;i++){
         if(mp.count(tmp))
             return i*m-mp[tmp];
         tmp=1LL*tmp*a%p;
     }
     return -;
 }

 int main(){
     while(~scanf("%d%d%d",&p,&a,&b)){
         int ans=BSGS();
         if(~ans)printf("%d\n",ans);
         else printf("no solution\n");
     }
 }

证明：

有这样一条式子：

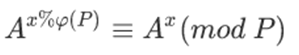
证明了这个就搞定了

处理一下这个式子：

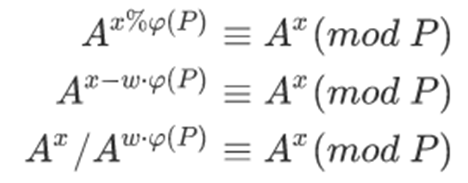
手头上的条件：gcd(A,P)=1
欧拉定理：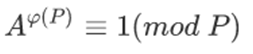

证完了OvO