SciTech-Mathmatics - Matrix Analysis(矩阵分析)-重要结论 + 特征值分解 + Matrix视为 Linear Space的 变换 与 运算 + 任两个Vectors可通过Matrix变换互相转化 + 方阵(满秩)不改变向量维数

SciTech-Mathmatics - Matrix Analysis:矩阵分析

Matrix Analysis 重要结论

\(\large \text{ Matrix Transformation }\)(矩阵变换) 亦为 \(\large \text{ Linear Transformation }\)(线性变换).

1. 要严格区分 Transformation(变换) 与 Function(函数):
   
   Functions(函数) 与 Transformation(变换)
2. Matrix视为"Linear Space"的"Transformation(变换)与Operation(运算)";
3. 同LinearSpace(线性空间)的"任意两个非零Vectors可通过"Matrix变换"互相转化;
4. "方阵(满秩)"不改变变换前后的两非零Vectors的"Dimensions(维数)"
5. "非方阵"变换改变(升或降)前后两非零Vectors的"Dimensions(维数)"

Linear Space + Vector + Matrix 视角

1. \(\large \text{Linear Space } \bf{K^n}\)上, 任一 \(\large \text{ Vector } \bf{ V_{a_{ n \times 1 }} }\) 通过 \(\large \text{ Matrix Transformation }\)后的 \(\large \text{ Vector } \bf{ V_{b_{n \times 1}} }\) 仍在同一 \(\large \bf{K^n}\)

2. \(\large \text{Linear Space } \bf{K^n}\)上, 任何两个 \(\large \text{ Vector } \bf{ V_{a_{n \times 1}} \neq 0 } \text{ 与 } \bf{ V_{b_{n \times 1}} \neq 0 }\) 都能通过一组合适的 \(\large \text{Fundamental Transformation } A_{n \times n}\) (基本线性变换) 实现互相转化, 即 \(\large \exists A_{n \times n} \in \bf{K^n} , \ 使\ A_{n \times n} \bf{ V_{a_{n \times 1}} } = \bf{ V_{b_{n \times 1}} }\) 。
   
   例如在 \(\large \text{Linear Space } \bf{R^2}(2D空间)\)上的 \(\large \text{Fundamental Transformation }\)(基本线性变换)只有 \(\large \bf{\text{ Rotation(旋转) } }\) 与 \(\large \bf{\text{ Scale(伸缩)} }\) 两种(后文有独立章节).

3. 任一\(\large \text{ Matrix Transformation }\) 都能
   
   分解为一组 \(\large \text{Fundamental Linear Transformation }\)(基本线性变换).

4. 两大类 \(\large \text{ Matrix Transformation }\)(矩阵变换)

   • 方阵(满秩) 这种特殊的 \(\large \text{ Matrix Transformation }\) 不改变变换前后 两个Vector的“Dimensions(维数)”。
     
     
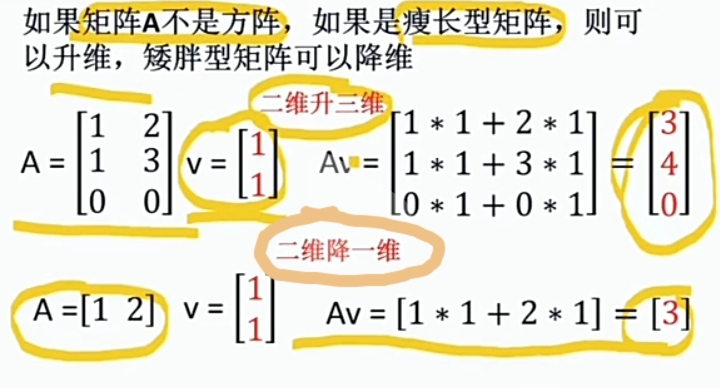
   • 非方阵 种类 \(\large \text{ Matrix Transformation }\) 升或降 Vector的Dimensions(维数)
     
     

方阵 的 Matrix Transformation

注意:

"非方阵"变换改变(升或降)前后两非零Vectors的"Dimensions(维数)".

\(\large \text{Fundamental Transformation }\)(基本的 线性变换):

1. \(\large \bf{ \text{Scale(伸缩)} }\) : \(\large Av = \lambda v = \lambda \bf{I} v\)
   
   \(\large (\bf{ \lambda I } - A) V = 0 \bf{\text{ 是 Eigenvalue Decomposition 的核心公式 } }\)
2. \(\large \bf{\text{ Rotation(旋转) } }\) : \(\large A^x v = \lambda v\)
   
   \(\large Vector\ V \text{ 作 } x \text{ 次 } Matrix \ Transformation\ A \text{ 就可能 } 与\ V\ \bf{方向重合}\)
   
   如$ x \text{ 依序取 } (1,2,\cdots, n)$ 时 $\large (\lambda \bf{I} - A^x) v $ 就可能趋近或等于 0。

\(\large \text{Possible Transformation }\)(可能的 线性变换):

\(\large \text{Linear Space } \bf{K^n}\)上, \(\large \bf{\text{ 方阵 A } }\) 对 任何一个 \(\large \text{ Vector } \bf{V}\), \(\large \bf{ 只有 } \text{ 三种线性变换的可能 }\):

• \(\large \text{Fundamental Transformation }\):
  
  \(\large \bf{ \text{Scale(伸缩)} }\) : \(\large Av = \lambda v = \lambda \bf{I} v\) 或 \(\large \bf{\text{ Rotation(旋转) } }\)
• \(\large \bf{\text{ Rotation(伸缩) } }\) 并且 \(\large \bf{\text{ Rotation(旋转) } }\)

\(\large \bf{ K^{n} } \text{ 的通用 } \bf{Scale} 及 Example(\bf{R^{2}})\)

\(\large \bf{K^{n}} \text{ 特征值分解 } 的 \bf{推导}\):

\(\large \begin{array}{ll} \because & A_{scale} V = \bf{ \lambda I } V = \bf{ \lambda } V \\ \therefore & \begin{cases} (\bf{ \lambda I } - A) V = 0, \ \text{ the } Characteristic\ Polynomial \text{ for matrix } A \\ |\bf{ \lambda I } - A| = 0 \end{cases} \end{array}\)

\(\large \begin{array}{ll} \\ \bf{注} & V = \begin{bmatrix} v_1 \\ \vdots \\ v_n \end{bmatrix} \bf{ \neq 0 } , where\ v_i \in K, \ i \in [1, n]. \\ & 即\ \bf{ V }\ 是 \text{非零} 的 \text{ 列向量 } \end{array}\)

\(\large \bf{K^{n}} \text{ 特征值分解 } 的 \bf{策略}\):

\(\large \begin{array}{ll} 1. & |\bf{ \lambda I } - A|=0 \Leftarrow \text{ 可先解出 } A \text{ 的所有 } Eigenvalues, \end{array}\)

\(\large \begin{array}{ll} 2. & (\bf{ \lambda I } - A) V = 0 \Leftarrow \text{ 一一代入 }Eigenvalue \text{ 得其所有 } Eigenvectors \end{array}\)

\(\large \bf{R^{2}} 的Example :\) 求 \(\large \begin{bmatrix} 1 & 2 \\ -1 & 4 \end{bmatrix}\) 全部 特征值和特征向量

\(\large \begin{array}{ll} \because & 0 = |\bf{ \lambda I } - A| = \begin{vmatrix} \lambda - 1 & 0-2 \\ 0-(-1) & \lambda - 4 \end{vmatrix} \\ & \ = \lambda^{2} -5\lambda + 6 = (\lambda-2)(\lambda -3) = 0 \\ \therefore & \bf{ \lambda = 2 \ or \ \lambda = 3 } \end{array}\)

\(\large \begin{array}{ll} let & V= \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} \bf{ \neq 0 }, \{v_i | v_i \in K, i \in \{1,2\}\}, \ 因为\text{ V 是非零列向量. } \end{array}\)

\(\large for \ Eigenvalue\ \lambda = 2 :\)

\(\large \begin{array}{ll} \because & (\bf{ \lambda I } - A) V = (\bf{ 2 I } - A) V = \begin{bmatrix} \lambda - 1 & 0-2 \\ 0-(-1) & \lambda - 4 \end{bmatrix} V \\ & = \begin{bmatrix} 1 & -2 \\ 1 & -2 \end{bmatrix} V = \begin{bmatrix} 1 & -2 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} v_1 - 2v_2 \\ 0 \end{bmatrix} = 0 \\ & \Rightarrow v_1 - 2v_2 = 0 , or \ v_1 = 2v_2, \text{ where } v_2 \text{ is a freedom variable } \\ & let \ V_{base} = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \\ \therefore & \text{All Eigenvectors for } \lambda = 2 \text{ are } \\ & \bf{ \{ V | V=k V_{base}, k \in K, k \neq 0, V_{base} = \begin{bmatrix} 2 \\ 1 \end{bmatrix} \} } \end{array}\)

\(\large for \ Eigenvalue\ \lambda = 3, \ Similarly:\)

\(\large \begin{array}{ll} \because & (\bf{ \lambda I } - A) V = (\bf{ 3 I } - A) V = \begin{bmatrix} \lambda - 1 & 0-2 \\ 0-(-1) & \lambda - 4 \end{bmatrix} V \\ & = \begin{bmatrix} 2 & -2 \\ 1 & -1 \end{bmatrix} V = \begin{bmatrix} 1 & -1 \\ 0 & 0 \end{bmatrix} \begin{bmatrix} v_1 \\ v_2 \end{bmatrix} = \begin{bmatrix} v_1 - v_2 \\ 0 \end{bmatrix} = 0 \\ & \Rightarrow v_1 - v_2 = 0 , or \ v_1 = v_2, \text{ where } v_2 \text{ is a freedom variable } \\ & let \ V_{base} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \\ \therefore & \text{All Eigenvectors for } \lambda = 3 \text{ are } \\ & \bf{ \{ V | V=k V_{base}, k \in K, k \neq 0 , V_{base} = \begin{bmatrix} 1 \\ 1 \end{bmatrix} \} } \end{array}\)

\(\large \bf{R^{2}} \text{ 的 } \bf{Fundamental\ Transformation }\)

$\large \ \bf{Scale(伸缩)} 及 \bf{Rotation(旋转)} $

例如在 \(\large \text{Linear Space } \bf{R^2}(2D空间)\)上, 任意一个\(\large \text{ Matrix Transformation }\)(矩阵线性变换)`都可分解为一组两种 \(\large \text{Fundamental Transformation }\)(基本线性变换):

• \(\large \bf{\text{向量 }} \Leftrightarrow \bf{\text{ 坐标 : } } let \ V = \begin{bmatrix} x \\ y \end{bmatrix} = \begin{bmatrix} r \ cos \alpha \\ r \ sin \alpha \end{bmatrix}\)

• \(\large \bf{\text{ Rotation(旋转) } }\)
  
  \(\large A_{rotate} = \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix}\),
  
  \(\large \begin{array}{lll} \\ \because & cos (\alpha + \theta) =& cos \alpha \ cos \theta - \ sin \alpha \ sin \theta \\ & sin(\alpha + \theta) =& sin \alpha \ cos \theta + \ cos \alpha \ sin \theta \end{array}\)
  
  \(\large \begin{array}{lll} \therefore & A_{rotate} V =& \begin{bmatrix} r \ cos (\alpha + \theta) \\ r \ sin(\alpha + \theta) \end{bmatrix} =& \begin{bmatrix} cos \theta & -sin \theta \\ sin \theta & cos \theta \end{bmatrix} \begin{bmatrix} r \ cos \alpha \\ r \ sin \alpha \end{bmatrix} \end{array}\)

• \(\large \bf{\text{ Scale(伸缩)} }\)
  
  \(\large A_{scale} = \bf{ \lambda } \begin{bmatrix} cos 0 & -sin 0 \\ sin 0 & cos 0 \end{bmatrix} = \bf{ \lambda I } = \bf{ \lambda } \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)

Matrix Analysis(矩阵分析学)

合成任意的目标 "Matrix Transformation(矩阵变换)"

目标函数\(\large \bf{ M_{n \times n} }\) 用Mathematical Analysis(数学分析)思想: 合成任意的目标 "Function(函数) 或Transformation(变换)". 以下都在 \(\large \text{Linear Space } \bf{K^n}\)上,

1. 因为 同LinearSpace(线性空间)的"任意两个非零Vectors可通过"Matrix变换"互相转化;
   • 设任意两个非零 \(\large \text{ Vectors } \bf{ V_{a_{n \times 1}} \neq 0 } \text{ 与 } \bf{ V_{b_{n \times 1}} \neq 0 }\),
     
     then, 存在目标 Matrix Transformation(矩阵变换) \(\large \bf{M_{n \times n}}\) 使得 \(\large \bf{ V_{b_{n \times 1}} = M_{n \times n} V_{ a_{n \times 1} } }\)
   • but, \(\large \text{Fundamental Transformation }\)(基本线性变换) 只有三种:
     
     \(\large \bf{ \text{Scale(伸缩)} }\), \(\large \bf{\text{ Rotation(旋转) } }\) 和 \(\large \bf{\text{ Scale }} \text{ and } \bf{ \text{ Rotation } }\)
   • 因此, 有必要用 \(\large \text{Fundamental Transformation }\) 合成任意的存在目标 Matrix Transformation(矩阵变换) \(\large \bf{M_{n \times n}}\).
     
     即，合成任意的\(\large \bf{ \text{Scale(伸缩)} }\), \(\large \bf{\text{ Rotation(旋转) } }\) 和 \(\large \bf{\text{ Rotation(伸缩) } }\) 并且 \(\large \bf{\text{ Rotation(旋转) } }\)
   • 分析函数式“合成”:
     
     既然，目标 Matrix Transformation(矩阵变换) \(\large \bf{ M_{n \times n} }\) 使得 \(\large \bf{ V_{b_{n \times 1}} = M_{n \times n} V_{a_{n \times 1}} }\)
     
     设 \(\large \bf{ A, \ shape 为(n \times n) }\) 代表一个 "基本矩阵(函数 或 变换)",
     
     则, 目标 Matrix Transformation(矩阵变换) \(\large \bf{ M, \ shape 为 (n \times n) }\) 可用 $ \bf{A} $ 的 Operations(运算) 合成(Approximation):
     
     例如，用“幂函数”(Operation为Multiplication)形式:
     
     假设，$\large \bf{M} = A^x $, 那e么 \(\large V_{b} = \bf{M} V_{a} = \bf{A^x} V_{a}\)
     
     

\(\large 图示 \bf{R^{2}} 的 \bf{Scale(伸缩)} ( \bf{特征值分解} )\)