Ice_cream's world I（并查集成环）

Problem Description

ice_cream's world is a rich country, it has many fertile lands. Today, the queen of ice_cream wants award land to diligent ACMers. So there are some watchtowers are set up, and wall between watchtowers be build, in order to partition the ice_cream’s world. But how many ACMers at most can be awarded by the queen is a big problem. One wall-surrounded land must be given to only one ACMer and no walls are crossed, if you can help the queen solve this problem, you will be get a land.

 

Input

In the case, first two integers N, M (N<=1000, M<=10000) is represent the number of watchtower and the number of wall. The watchtower numbered from 0 to N-1. Next following M lines, every line contain two integers A, B mean between A and B has a wall(A and B are distinct). Terminate by end of file.

 

Output

Output the maximum number of ACMers who will be awarded.
One answer one line.

 

Sample Input

8 10
0 1
1 2
1 3
2 4
3 4
0 5
5 6
6 7
3 6
4 7

 

Sample Output

3

 

Source

HDU 2007-10 Programming Contest_WarmUp

分析：并查集成环问题。。关于并查集理解了为什么能判断成环，首先并查集我们知道能够判断两个点是否属于同一个集合，并且将不属于同一个集合中的点归纳到同一个集合中去。。。

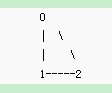
这个图有环是已知的吧，但是要用代码来判断，就很复杂，首先我们把每个点看成独立的集合{0} ，{1}， {2}, 然后规定如果两个点之间有边相连，如果这两个点不属于同一个集合，那就将他们所属的结合合并，看边0-1，直接将这两个点代表的集合合并{0， 1}, 其中让1来当父节点， 看边1-2， 它们分别属于不同的集合，合并集合之后是{1， 2}，让2来当父节点，依照这种逻辑关系，0的祖先节点就是2， 然后在看边0-2，他们属于一个集合，因为他们有着共同的祖先2，
这就说明0-2之间在没有0-2这条边之前已经连通了，如果在加上这条边的话那从0到2就有两条路径可达，就说明存在一个环了。。。这就是并查集所谓的成环的实质。。。

 // /*并查集*/
 // int prev[1000];

 // int find(int x){//查找我的掌门
 //     int r=x;    //委托r去找掌门
 //     while(prev[r]!=r){//如果r的上级不是自己（也就是说他找到的大侠不是掌门）
 //         r=prev[r];//r就接着找他的掌门，直到到掌门为止
 //     }
 //     return r;//掌门驾到~~~~
 // }

 // void join(int x,int y){//联通
 //     int fx=find(x);
 //     int fy=find(y);

 //     if(fx!=fy){
 //         prev[fx]=fy;
 //     }

 // }
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 using namespace std;

 const int maxn = 1e3+;
 int pre[maxn];
 int cnt=;

 int Find(int x){
     int u=x;
     while(u!=pre[u]){
         u=pre[u];
     }
     int i=x,j;
     while(pre[i]!=u){/*压缩路径*/
         j=pre[i];
         pre[i]=u;
         i=j;
     }
     return u;
 }

 void mix(int u,int v){
     int fu=Find(u);
     int fv=Find(v);
     if(fu!=fv){
         pre[fu]=fv;
     }
     else{
         cnt++;
     }
 }

 int main(int argc, char const *argv[])
 {
     int n,m;
      while(~scanf("%d %d",&n,&m)){
          cnt=;
         for( int i=; i<n; i++ ){/*初始化*/
             pre[i]=i;
         }
         for( int i=; i<m; i++ ){
             int a,b;
             cin>>a>>b;
             mix(a,b);
         }
         cout<<cnt<<endl;
     }
     return ;
 }