sklearn LDA降维算法
sklearn LDA降维算法
LDA(Linear Discriminant Analysis)线性判断别分析,可以用于降维和分类。其基本思想是类内散度尽可能小,类间散度尽可能大,是一种经典的监督式降维/分类技术。
sklearn代码实现
#coding=utf-8
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn import datasets
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
import numpy as np
def main():
iris = datasets.load_iris() #典型分类数据模型
#这里我们数据统一用pandas处理
data = pd.DataFrame(iris.data, columns=iris.feature_names)
data['class'] = iris.target
#这里只取两类
# data = data[data['class']!=2]
#为了可视化方便,这里取两个属性为例
X = data[data.columns.drop('class')]
Y = data['class']
#划分数据集
X_train, X_test, Y_train, Y_test =train_test_split(X, Y)
lda = LinearDiscriminantAnalysis(n_components=2)
lda.fit(X_train, Y_train)
#显示训练结果
print lda.means_ #中心点
print lda.score(X_test, Y_test) #score是指分类的正确率
print lda.scalings_ #score是指分类的正确率
X_2d = lda.transform(X) #现在已经降到二维X_2d=np.dot(X-lda.xbar_,lda.scalings_)
#对于二维数据,我们做个可视化
#区域划分
lda.fit(X_2d,Y)
h = 0.02
x_min, x_max = X_2d[:, 0].min() - 1, X_2d[:, 0].max() + 1
y_min, y_max = X_2d[:, 1].min() - 1, X_2d[:, 1].max() + 1
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
Z = lda.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.Paired)
#做出原来的散点图
class1_x = X_2d[Y==0,0]
class1_y = X_2d[Y==0,1]
l1 = plt.scatter(class1_x,class1_y,color='b',label=iris.target_names[0])
class1_x = X_2d[Y==1,0]
class1_y = X_2d[Y==1,1]
l2 = plt.scatter(class1_x,class1_y,color='y',label=iris.target_names[1])
class1_x = X_2d[Y==2,0]
class1_y = X_2d[Y==2,1]
l3 = plt.scatter(class1_x,class1_y,color='r',label=iris.target_names[2])
plt.legend(handles = [l1, l2, l3], loc = 'best')
plt.grid(True)
plt.show()
if __name__ == '__main__':
main()
测试结果
Means: #各类的中心点
[[ 5.00810811 3.41891892 1.44594595 0.23513514]
[ 6.06410256 2.80769231 4.32564103 1.33589744]
[ 6.61666667 2.97222222 5.63055556 2.02777778]]
Score: #对于测试集的正确率
0.973684210526
Scalings:
[[ 1.19870893 0.76465114]
[ 1.20339741 -2.46937995]
[-2.55937543 0.42562073]
[-2.77824826 -2.4470865 ]]
Xbar:
[ 5.89285714 3.0625 3.79375 1.19464286]
#X'=np.dot(X-lda.xbar_,lda.scalings_)默认的线性变化方程
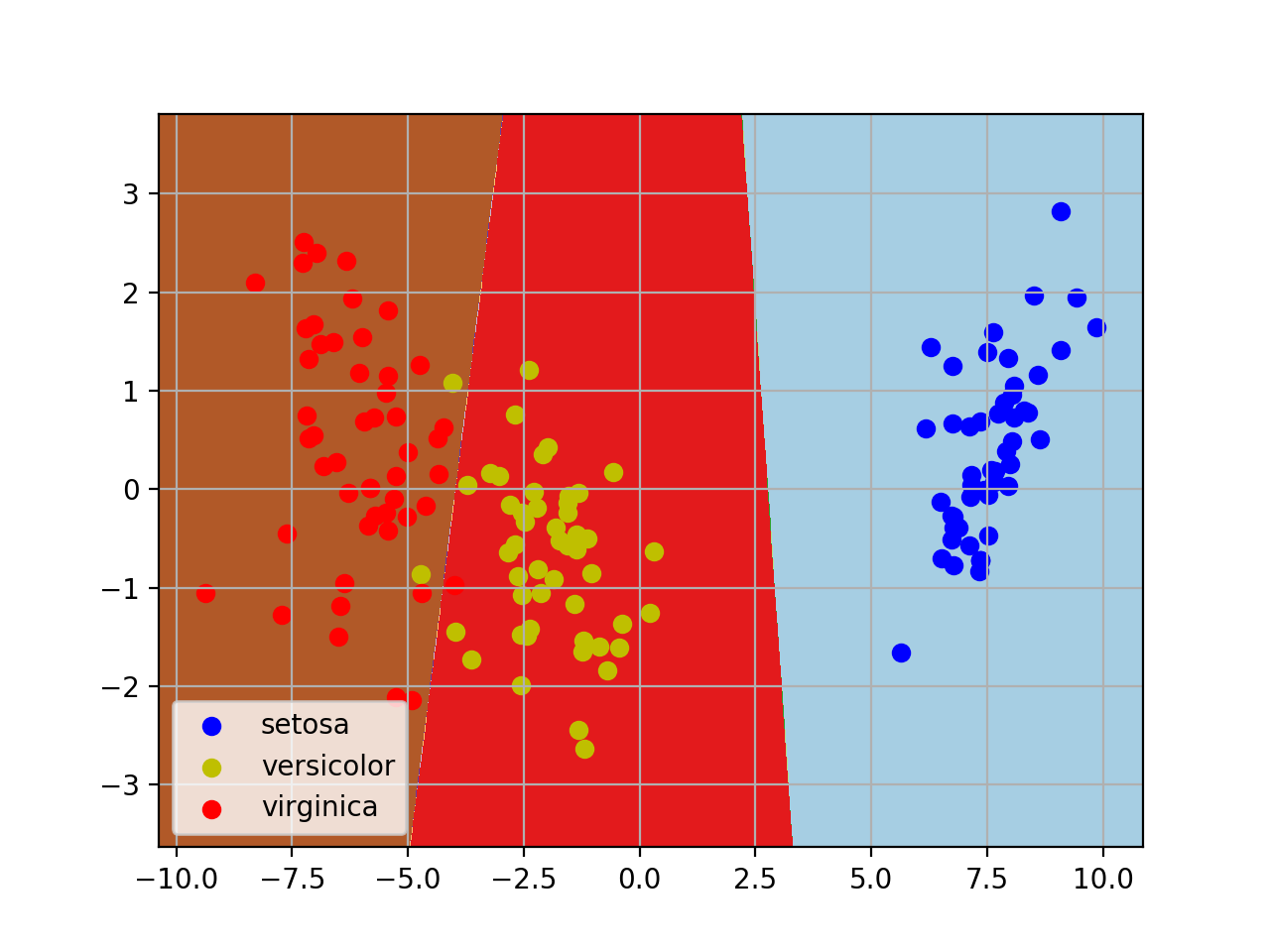
sklearn LDA降维算法的更多相关文章
- 机器学习实战基础(二十):sklearn中的降维算法PCA和SVD(一) 之 概述
概述 1 从什么叫“维度”说开来 我们不断提到一些语言,比如说:随机森林是通过随机抽取特征来建树,以避免高维计算:再比如说,sklearn中导入特征矩阵,必须是至少二维:上周我们讲解特征工程,还特地提 ...
- 降维算法整理--- PCA、KPCA、LDA、MDS、LLE 等
转自github: https://github.com/heucoder/dimensionality_reduction_alo_codes 网上关于各种降维算法的资料参差不齐,同时大部分不提供源 ...
- 参考:菜菜的sklearn教学之降维算法.pdf!!
PCA(主成分分析法) 1. PCA(最大化方差定义或者最小化投影误差定义)是一种无监督算法,也就是我们不需要标签也能对数据做降维,这就使得其应用范围更加广泛了.那么PCA的核心思想是什么呢? 例如D ...
- 四大机器学习降维算法:PCA、LDA、LLE、Laplacian Eigenmaps
四大机器学习降维算法:PCA.LDA.LLE.Laplacian Eigenmaps 机器学习领域中所谓的降维就是指采用某种映射方法,将原高维空间中的数据点映射到低维度的空间中.降维的本质是学习一个映 ...
- ML: 降维算法-LDA
判别分析(discriminant analysis)是一种分类技术.它通过一个已知类别的“训练样本”来建立判别准则,并通过预测变量来为未知类别的数据进行分类.判别分析的方法大体上有三类,即Fishe ...
- 【转】四大机器学习降维算法:PCA、LDA、LLE、Laplacian Eigenmaps
最近在找降维的解决方案中,发现了下面的思路,后面可以按照这思路进行尝试下: 链接:http://www.36dsj.com/archives/26723 引言 机器学习领域中所谓的降维就是指采用某种映 ...
- 机器学习实战基础(二十三):sklearn中的降维算法PCA和SVD(四) PCA与SVD 之 PCA中的SVD
PCA中的SVD 1 PCA中的SVD哪里来? 细心的小伙伴可能注意到了,svd_solver是奇异值分解器的意思,为什么PCA算法下面会有有关奇异值分解的参数?不是两种算法么?我们之前曾经提到过,P ...
- 机器学习实战基础(二十一):sklearn中的降维算法PCA和SVD(二) PCA与SVD 之 降维究竟是怎样实现
简述 在降维过程中,我们会减少特征的数量,这意味着删除数据,数据量变少则表示模型可以获取的信息会变少,模型的表现可能会因此受影响.同时,在高维数据中,必然有一些特征是不带有有效的信息的(比如噪音),或 ...
- 用scikit-learn进行LDA降维
在线性判别分析LDA原理总结中,我们对LDA降维的原理做了总结,这里我们就对scikit-learn中LDA的降维使用做一个总结. 1. 对scikit-learn中LDA类概述 在scikit-le ...
随机推荐
- PAT Basic 1073. 多选题常见计分法
题目内容 多选题常见计分法(20) 时间限制 400 ms 内存限制 65536 kB 代码长度限制 8000 B 判题程序 Standard 作者 CHEN, Yue 批改多选题是比较麻烦的事情,有 ...
- Hbase启动hbase shell运行命令报Class path contains multiple SLF4J bindings.错误
1:Hbase启动hbase shell运行命令报Class path contains multiple SLF4J bindings.错误,是因为jar包冲突了,所以对于和hadoop的jar包冲 ...
- 浅析H5图片上传
概述 最近需求上需要实现图片上传的功能,简单记录下实现过程.目前实现的功能比较简单,主要有以下几点: 图片预览 图片删除 拖拽上传 压缩上传 移动端实现方案:使用File API 主要使用到 File ...
- linux 运维一些常见的简单安全设置 运维必看
1. 修改ssh服务的默认端口,这个是十分有必要的,因为密码爆破一直存在.ssh服务的默认端口是22,一般的恶意用户也往往扫描或尝试连接22端口.所以第一步就是修改这个默认端口打开/etc/ssh/s ...
- gcc make 与cmake
1. gcc (1)是什么? 它是GNU Compiler Collection(就是GNU编译器套件),也可以简单认为是编译器.它可以编译很多种编程语言(括C.C++.Objective-C.For ...
- rxjs简单入门
rxjs全名Reactive Extensions for JavaScript,Javascript的响应式扩展, 响应式的思路是把随时间不断变化的数据.状态.事件等等转成可被观察的序列(Obser ...
- Codeforces Gym100543B 计算几何 凸包 线段树 二分/三分 卡常
原文链接https://www.cnblogs.com/zhouzhendong/p/CF-Gym100543B.html 题目传送门 - CF-Gym100543B 题意 给定一个折线图,对于每一条 ...
- 存储过程导入excel
#region 导入订单 protected override string DoExcelData(System.Data.DataTable dt) { ...
- 如何在不使用try语句的情况下查看文件是否存在
如果你要确定文件存在的话然后做些什么,那么使用try是最好不过的 如果您不打算立即打开文件,则可以使用os.path.isfile检查文件 如果path是现有常规文件,则返回true.对于相同的路径, ...
- 035 控制并发 select * from test1 where id =1 for update 就会对这行加锁了?
今天在看同事程序的时候,看到这种用法,顺便学习下. 一:理论 1.功能 这个功能是上锁. 上的是一个排它锁,也就是说,其他的事务是可以读取的.但是不能写入或者更新. 二:实践 1.创建表 2.提交一条 ...
