求LCA最近公共祖先的在线ST算法_C++

　　ST算法是求最近公共祖先的一种 在线 算法，基于RMQ算法，本代码用双链树存树

　　预处理的时间复杂度是 O(nlog₂n)   查询时间是 O(1) 的

　　另附上离线算法 Tarjan 的链接：

　　　　http://www.cnblogs.com/hadilo/p/5840390.html

---

　　首先预处理出深度，以及 DFS 序，这里的DFS序是指回溯时也算上，比如

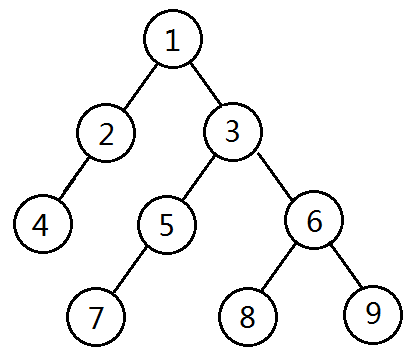
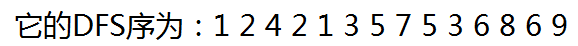
 void dfs(int x,int dep)
 {
     int i;
     d[x]=dep;
     a[++top]=x;
     for (i=down[x];i!=;i=next[i])
     {
         dfs(i,dep+);
         a[++top]=x;
     }
 }

　　然后记录每个节点在 DFS 序中第一次出现的位置，b[i] 为第 i 号节点第一次出现的位置

     for (i=;i<=top;i++) if (b[a[i]]==) b[a[i]]=i;

---

　　开始 DP 处理区间区间内最小值，这里使用 RMQ 算法，其功能类似于线段树或树状数组

　　f[i][j] 表示从第 i 位开始，连续 2^j 个数的最小值，状态转移：

     f[i][j]=min(f[i][j-],f[i+(<<(j-))][j-])

　　因为它是 2 的幂次方的状态，所以每次转移可以看做把当前状态分为两个相等的部分，求两部分的最小值

　　如： 5 7 3 2   和   4 6 1 5

　　　　 min=2           min=1

　即 f[1][2]=2       f[5][2]=1

　　所以 f[1][3]=min(f[1][2],f[5][2])=1

　　初始状态：f[i][0]=d[a[i]]    loc[i][0]=a[i]

　　注意这里 f 记录的是它的深度的最小值，而位置用 loc 记录

 void init()
 {
     int i,j,s,x,k;
     for (i=;i<=top;i++)
     {
         f[i][]=d[a[i]];
         loc[i][]=a[i];
     }
     s=log2(top);
     for (j=;j<=s;j++)
     {
         k=top-(<<j)+;
         for (i=;i<=k;i++)
         {
             x=i+(<<(j-));
             if (f[i][j-]<=f[x][j-])
             {
                 f[i][j]=f[i][j-];
                 loc[i][j]=loc[i][j-];
             }
             else
             {
                 f[i][j]=f[x][j-];
                 loc[i][j]=loc[x][j-];
             }
         }
     }
 }

　　代码用变量优化了一下常数

---

　　接着开始进行询问

　　读入两个节点，查询它们第一次出现的位置

　　在这两个位置之间的区间查询最小深度的节点，该节点即为最近公共祖先

　　查询区间时，我们把它分成两个部分，可以有重叠，如

　　　　8 9 6 5 6 8 4

　　这7个节点，把它分成： 8 9 6 5  和 5 6 8 4

　　　　　　　　　　　　　 min=5      min=4

　　则最小值为 min(5,4)=4

     min(f[x][log2(y-x)],f[y-(<<i)+][log2(y-x)]);

　　可以这样理解：

　　　　将两个位置的距离取个对数记为 i，然后从最左边，往后共 2ⁱ 个数的最小值，这是第一部分

　　　　第二个部分是从右边往左推 2ⁱ 个数，即 y-2ⁱ+1，然后再往后取 2ⁱ 个数

　　成功将区间分为两部分

     scanf("%d",&t);
     while (t>)
     {
         t--;
         scanf("%d%d",&x,&y);
         x=b[x];
         y=b[y];
         if (x>y) swap(x,y);
         i=log2(y-x);
         k=y-(<<i)+;
         printf("%d\n",f[x][i]<f[k][i]?loc[x][i]:loc[k][i]);
     }

---

　　代码内有常数优化，有的地方思路可能不是很清晰，请谅解

　　给个完整代码

 #include<cstdio>
 #include<cstdlib>
 #include<cstring>
 #include<cmath>
 #include<iostream>
 #include<algorithm>
 #define N 100001
 using namespace std;

 int a[N*],d[N],down[N],next[N],top,f[*N][],loc[*N][],n,b[N];
 int log2(int x)
 {
     int k=;
     while (x>)
     {
         x/=;
         k++;
     }
     return k;
 }
 void dfs(int x,int dep)
 {
     int i;
     d[x]=dep;
     a[++top]=x;
     for (i=down[x];i!=;i=next[i])
     {
         dfs(i,dep+);
         a[++top]=x;
     }
 }
 void init()
 {
     int i,j,s,x,k;
     for (i=;i<=top;i++)
     {
         f[i][]=d[a[i]];
         loc[i][]=a[i];
     }
     s=log2(top);
     for (j=;j<=s;j++)
     {
         k=top-(<<j)+;
         for (i=;i<=k;i++)
         {
             x=i+(<<(j-));
             if (f[i][j-]<=f[x][j-])
             {
                 f[i][j]=f[i][j-];
                 loc[i][j]=loc[i][j-];
             }
             else
             {
                 f[i][j]=f[x][j-];
                 loc[i][j]=loc[x][j-];
             }
         }
     }
 }
 int main()
 {
     int i,k,x,y,t;
     scanf("%d",&n);
     for (i=;i<=n;i++) down[i]=d[i]=next[i]=;
     for (i=;i<=n;i++)
     {
         scanf("%d",&x);
         next[i]=down[x];
         down[x]=i;
     }
     top=;
     dfs(down[],);
     for (i=;i<=top;i++) if (b[a[i]]==) b[a[i]]=i;
     init();
     scanf("%d",&t);
     while (t>)
     {
         t--;
         scanf("%d%d",&x,&y);
         x=b[x];
         y=b[y];
         if (x>y) swap(x,y);
         i=log2(y-x);
         k=y-(<<i)+;
         printf("%d\n",f[x][i]<f[k][i]?loc[x][i]:loc[k][i]);
     }
     return ;
 }

版权所有，转载请联系作者，违者必究

QQ：740929894