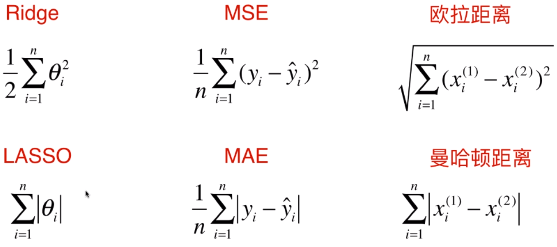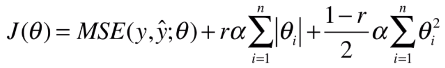机器学习:模型泛化(L1、L2 和弹性网络)
一、岭回归和 LASSO 回归的推导过程
1)岭回归和LASSO回归都是解决模型训练过程中的过拟合问题
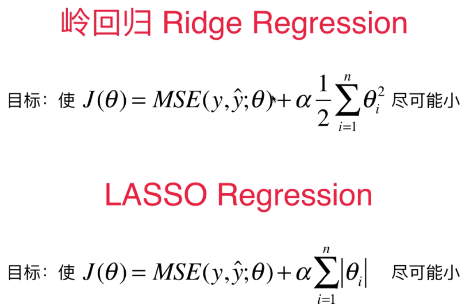
- 具体操作:在原始的损失函数后添加正则项,来尽量的减小模型学习到的 θ 的大小,使得模型的泛化能力更强;
2)比较 Ridge 和 LASSO
- 名词
Ridge、LASSO:衡量模型正则化;
MSE、MAE:衡量回归结果的好坏;
欧拉距离、曼哈顿距离:衡量两点之间距离的大小;
- 理解
- Ridge、LASSO:在损失函数后添加的正则项不同;
- MSE、MAE:两种误差的表现形式与对应的 Ridge 和 LASSO 的两种正则项的形式很像;
- 欧拉距离、曼哈顿距离:欧拉距离和曼哈顿距离的整体表现形式,与 Ridge、LASSO 两种正则项的形式也很像;
其它
- 在机器学习领域,对于不同的应用会有不同的名词来表达不同的衡量标准,但其背后本质的数学思想非常相近,表达出的数学的含义也近乎一致,只不过应用在了不同的场景中而产生了不同的效果,进而生成了不同的名词;
3)明科夫斯基距离
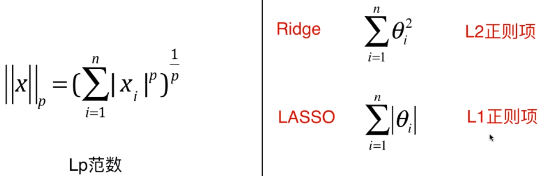
- 明科夫斯基距离:
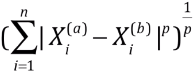
- 将明科夫斯基距离泛化:Lp 范数
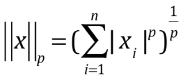
- p = 1:称为 L1 范数,相当于从 (0, 0) 点到 X 向量的曼哈顿距离;
- p = 2:称为 L2 范数,相当于从 (0, 0) 点到 X 向量的欧拉距离;
4)L1 正则、L2 正则
- Ridge 回归中添加了 L2 正则项,LASSO 回归中添加了 L1 正则项;
- L2 正则项和 L2 范数的区别在于,L2 正则项没有开平方,但有时候也直接称 L2 正则项为 L2 范数;(同理 L1 范数与 L1 正则项的关系)
- 原因: L2 正则项是用于放在损失函数中进行最优化,如果将 L2 正则项加上开根号,不会影响损失函数优化的最终结果,但是不带根号会显得整个式子更加简单,所以对于 L2 正则项的式子中不带根号;
- 同理在数学理论上也存在 Ln 正则项;
5)L0 正则
- 目的:使 θ 的个数尽量少,进而限制 θ,使得拟合曲线上下抖动幅度不要太大,模型的泛化能力也会得以提高;
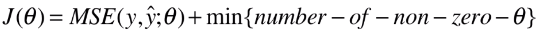
- L0 的正则项:描述非 0 的 θ 参数的个数;
- 实际中很少使用 L0 正则来进行模型正则化的过程,而是用 L1 正则代替;
- 原因: L0 正则的优化是一个 NP 难的问题;它不能使用诸如梯度下降法,甚至是直接求出一个数学公式这样的方式来直接找到最优解; L0 正则项本质是一个离散最优化的问题,可能需要穷举所有的让各种 θ 的组合为 0 的可能情况,然后依次来计算 J(θ) ,进而来觉得让哪些 θ 为 0 哪些 θ 不为 0,所以说 L0 正则的优化是一个 NP 难的问题;
- 如果想限制 θ 的个数,通常使用 L1 正则;
二、弹性网(Elastic Net)
1)公式
- 功能:也是解决模型训练过程中的过拟合问题;
- 操作:在损失函数后添加 L1 正则项和 L2 正则项;
- 特点:同时结合了 岭回归和 LASSO 回归的优势;
- r:新的超参数,表示添加的两个正则项的比例(分别为 r、1-r );
2)现实中,在进行正则化的过程中,通常要先使用 岭回归
- 优点:岭回归计算更精准;
- 缺点:不具有特征选择的功能;
- 原因:如果特征非常多的话,岭回归不能将某些 θ 设置为 0,若 θ 的量太大的话到导致整体计算量也非常的大;
3)当特征非常多时,应先考虑使用 弹性网
- 原因:弹性网结合了岭回归的计算的优点,同时又结合了 LASSO 回归特征选择的优势;
三、总结与开拓
1)总结
- 训练的机器学习模型不是为了在训练数据集上有好的测试结果,而是希望在未来面对未知的数据集上有非常好的结果;
- 模型在面对未知数据集表现的能力,为该模型的泛化能力;(模型泛化是机器学习领域非常非常重要的话题)
- 分析和提升模型泛化能力的方法:
- 看学习曲线;
- 对模型进行交叉验证;
- 对模型进行正则化;
2)开拓
- LASSO 回归的缺点:急于将某些 θ 化为 0,过程中可能会产生一些错误,使得最终的模型的偏差比较大;
- 问题:LASSO 回归在模型优化的过程中是有选择的将某些 θ 化为 0 吗?或者说有没有什么条件使得尽量避免让相关性比较强的特征的系数化为 0 ?还是说这一行为只是单纯的数学运算,就为目标函数尽量达到目标状态?
- “可能产生的错误”:将一些相关性比较强的特征的参数 θ 也化为 0,导致该特征丢失;
- 开拓思路
- 弹性网结合了岭回归和 LASSO 回归二者的优势,小批量梯度下降法结合了批量梯度下降法和随机批量梯度下降法二者的优势,类似的方法在机器学习领域经常被运用,用来创造出新的方法。
- 打个比方理解机器学习
- 参加考试前要做很多练习题,练习题就相当于训练数据,目的不是为了在做练习题的过程中达到满分,而是通过做练习题让我们在面对新的考试题时得到更高的分数,考试中面对的新的题目相当于模型在未来生成环境中见到的新的数据。
机器学习:模型泛化(L1、L2 和弹性网络)的更多相关文章
- 【笔记】简谈L1正则项L2正则和弹性网络
L1,L2,以及弹性网络 前情提要: 模型泛化与岭回归与LASSO 正则 ridge和lasso的后面添加的式子的格式上其实和MSE,MAE,以及欧拉距离和曼哈顿距离是非常像的 虽然应用场景不同,但是 ...
- ML-线性模型 泛化优化 之 L1 L2 正则化
认识 L1, L2 从效果上来看, 正则化通过, 对ML的算法的任意修改, 达到减少泛化错误, 但不减少训练误差的方式的统称 训练误差 这个就损失函数什么的, 很好理解. 泛化错误 假设 我们知道 预 ...
- 机器学习中模型泛化能力和过拟合现象(overfitting)的矛盾、以及其主要缓解方法正则化技术原理初探
1. 偏差与方差 - 机器学习算法泛化性能分析 在一个项目中,我们通过设计和训练得到了一个model,该model的泛化可能很好,也可能不尽如人意,其背后的决定因素是什么呢?或者说我们可以从哪些方面去 ...
- 机器学习中的L1、L2正则化
目录 1. 什么是正则化?正则化有什么作用? 1.1 什么是正则化? 1.2 正则化有什么作用? 2. L1,L2正则化? 2.1 L1.L2范数 2.2 监督学习中的L1.L2正则化 3. L1.L ...
- 机器学习中L1,L2正则化项
搞过机器学习的同学都知道,L1正则就是绝对值的方式,而L2正则是平方和的形式.L1能产生稀疏的特征,这对大规模的机器学习灰常灰常重要.但是L1的求解过程,实在是太过蛋疼.所以即使L1能产生稀疏特征,不 ...
- 机器学习 - 正则化L1 L2
L1 L2 Regularization 表示方式: $L_2\text{ regularization term} = ||\boldsymbol w||_2^2 = {w_1^2 + w_2^2 ...
- 斯坦福经典AI课程CS 221官方笔记来了!机器学习模型、贝叶斯网络等重点速查...
[导读]斯坦福大学的人工智能课程"CS 221"至今仍然是人工智能学习课程的经典之一.为了方便广大不能亲临现场听讲的同学,课程官方推出了课程笔记CheatSheet,涵盖4大类模型 ...
- L1&L2 Regularization的原理
L1&L2 Regularization 正则化方法:防止过拟合,提高泛化能力 在训练数据不够多时,或者overtraining时,常常会导致overfitting(过拟合).其直观的表现 ...
- L0/L1/L2范数的联系与区别
L0/L1/L2范数的联系与区别 标签(空格分隔): 机器学习 最近快被各大公司的笔试题淹没了,其中有一道题是从贝叶斯先验,优化等各个方面比较L0.L1.L2范数的联系与区别. L0范数 L0范数表示 ...
随机推荐
- Maximum Subsequence Sum【最大连续子序列+树状数组解决】
Problem Description 给定K个整数的序列{ N1, N2, ..., NK },其任意连续子序列可表示为{ Ni, Ni+1, ..., Nj },其中 1 <= i < ...
- C++中随机数的生成
1.随机数由生成器和分布器结合产生 生成器generator:能够产生离散的等可能分布数值 分布器distributions: 能够把generator产生的均匀分布值映射到其他常见分布,如均匀分布u ...
- MySql数据库的主从配置
主服务器 192.168.7.182 Centos6.5 MYSQL5.6.10 从服务器 192.168.112.7 Centos6.5 MYSQL5.6.10 主服务器配置(192.168.7.1 ...
- mysql一次运行多个SQL文件
在文件 batch.sql 中写下多个SQL文件 source file1.SQLsource file2.SQLsource file3.SQL 然后运行 source batch.sql
- MySQL数据库设置主从同步
MySQL主从同步的机制: MySQL同步的流程大致如下: 1.主服务器(master)将变更事件(更新.删除.表结构改变等等)写入二进制日志(master log). 2.从服务器(slave)的I ...
- numpy里*与dot与multiply
一.* , dot() multiply() 1, 对于array来说,(* 和 dot()运算不同, * 和 multiply()运算相同) *和multiply() 是每个元素对应相乘 do ...
- LAMP环境搭建问题
//////////////////////////LAMP环境搭建问题///////////////////////////////////////LAMP常见的问题A.安装相关问题(1)MySQL ...
- C++Builder XE5对于C++11的支持真蛋疼
好不容易下载个XE5,安装,破解,准备测试一下C++11中的lambda,写了一个最简单的表达式: [](){}; 居然编译通不过. 查了帮助文档,才晓得它的编译器分为BCC32和BCC64, BCC ...
- asp.net上传文件大小限制
<system.webServer> <security> <requestFiltering> <requestLimits maxAllowedConte ...
- filter()和sort()这两个方法一块学习,案例中。
<!doctype html> <html lang="en"> <head> <meta charset="UTF-8&quo ...