【Validation】林轩田机器学习基石

这一节主要讲如何通过数据来合理的验证模型好不好。

首先，否定了Ein来选模型和Etest来选模型。

（1）模型越复杂，Ein肯定越好；但是Eout就不一定了（见上一节的overfitting等）

（2）Etest是偷窥训练集，也没有效果

下面，集中讨论已有的数据集切分成train data和test data，怎么切分，怎么验证最合理。

Model Selection的流程如下：

（1）切分数据，选一个Eval最小的

（2）再用全量数据去训练选出来的那个model

流程搞清楚了，接下来就要看怎么切数据（怎么选K）

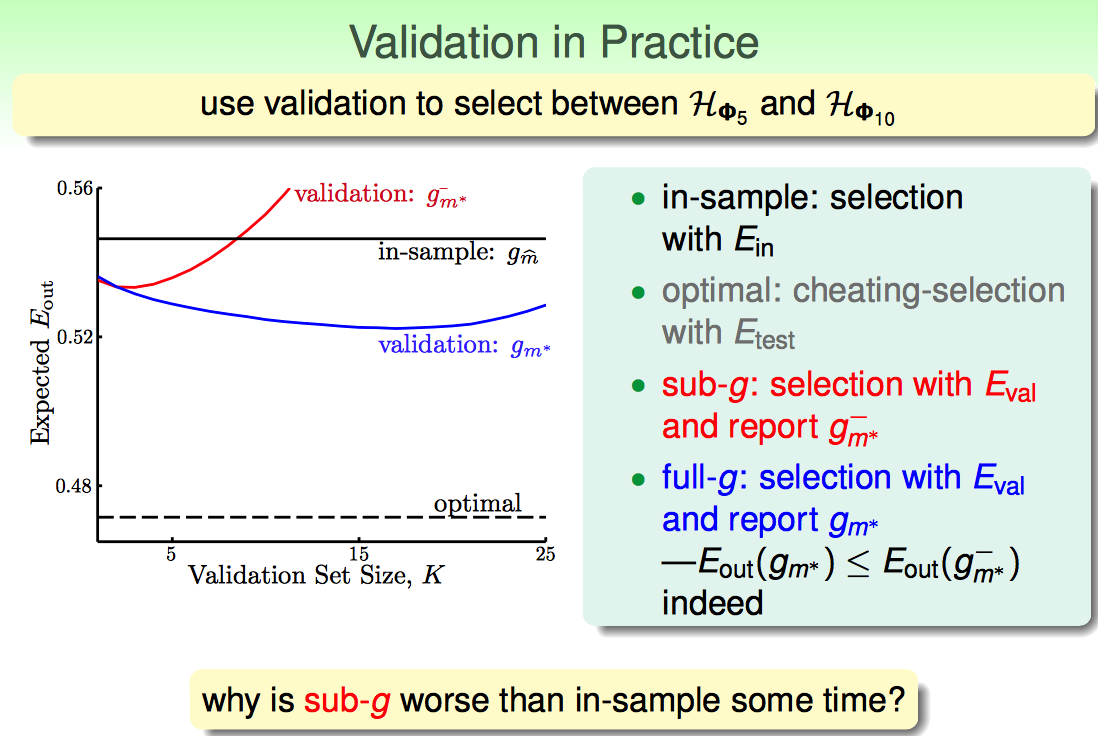
随着K增大，观察蓝线的变化趋势（因为蓝线是上边流程中应用的最终选出来模型的方法）: K太小了，Eval跟Eout差距太大（因为有Finite-Hoeffding的不等式）；K选择太大了，也不好，因为训练的数据太少了，效果肯定差。

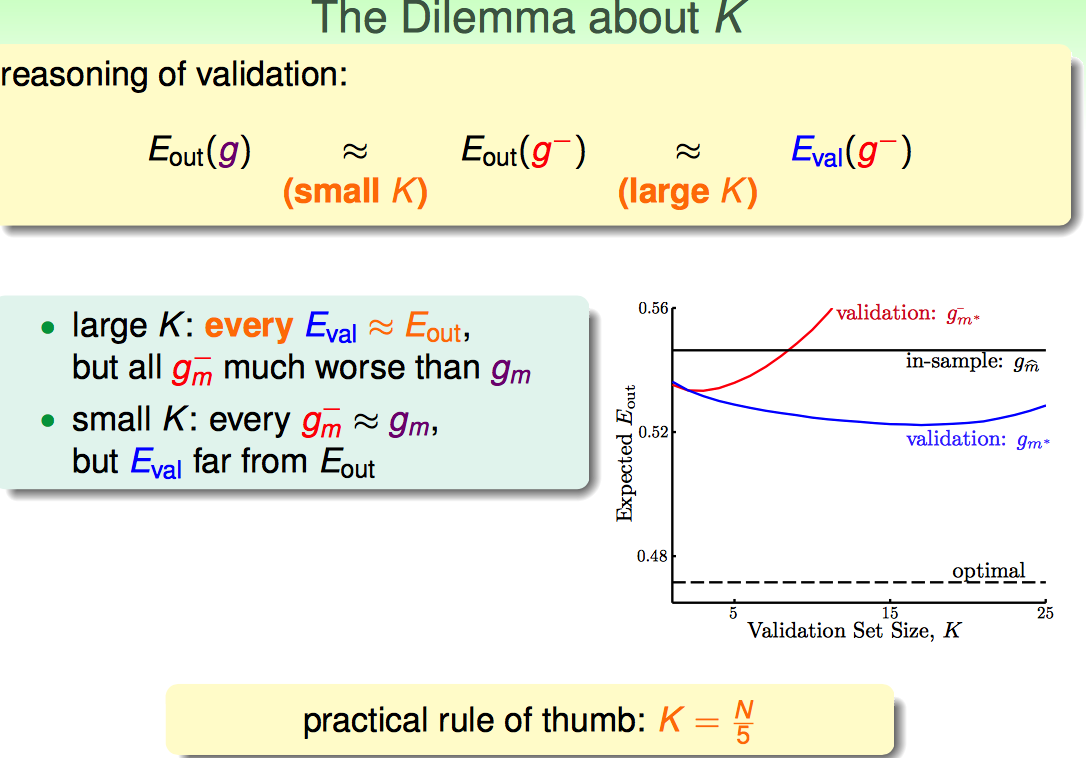
实际中取K=N/5作为经验值。

但上面的这种方法，毕竟只用一部分数据作为测试，效果容易不太稳定。所以才有了V-Fold cross validation。

最极端的情况是leave-one-out Estimate

这种情况基本是Eout的无偏估计，但是代价太高，不可行。

折中一下，10-fold cross validation是常用的方法。