二叉索引树，LA2191，LA5902，LA4329

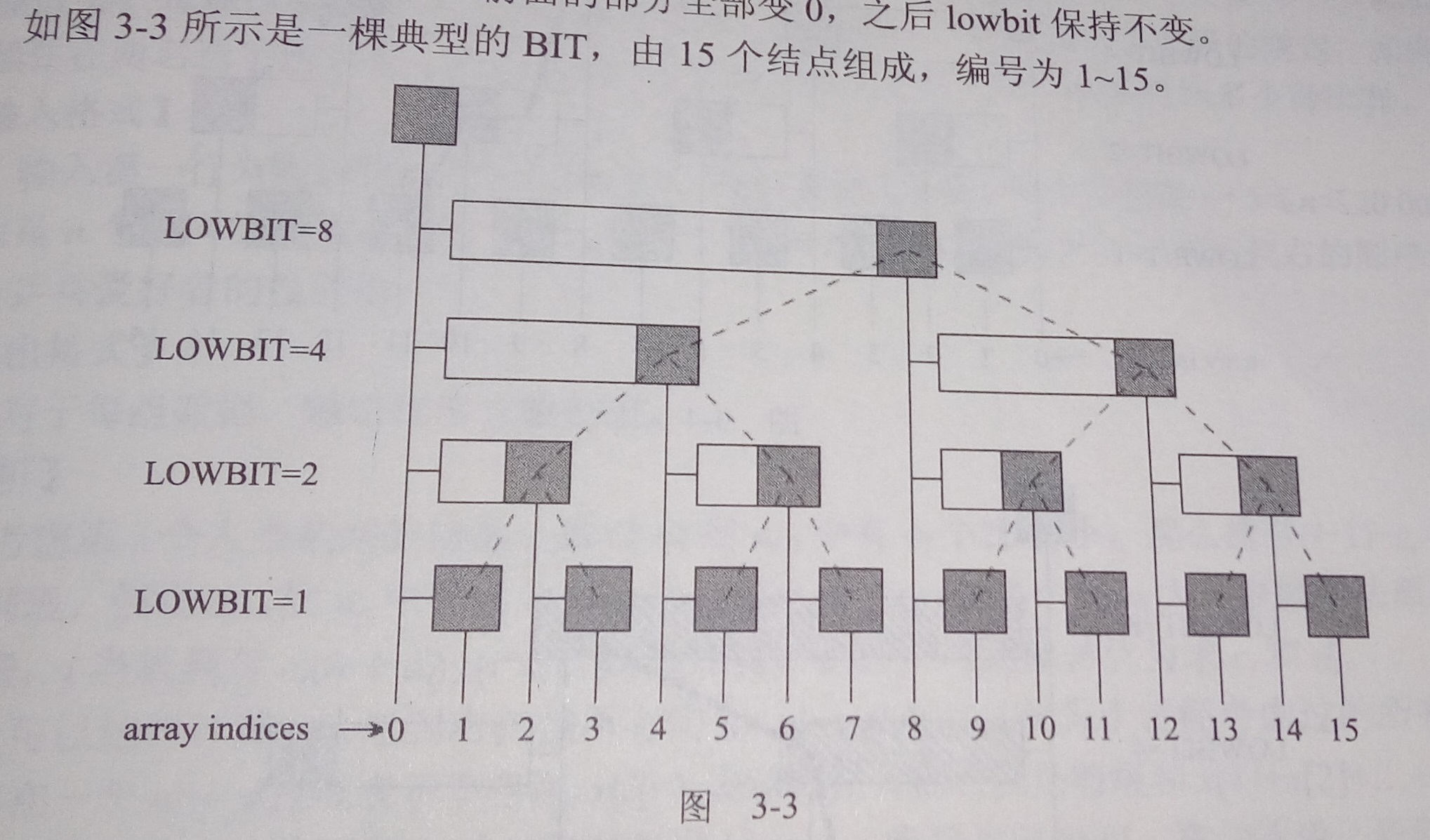
利用了二进制，二分的思想的一个很巧妙的数据结构，一个lowbit(x):二进制表示下的最右边的一个1开始对应的数值。

那么如果一个节点的为x左孩子，父亲节点就是 x + lowbit(x)，如果是右孩子，父亲节点是 x-lowbit(x)；

图中白条部分就是辅助数组C对应的最底下的和。

1、那么一个前缀和有是怎样的呢？

　　就是从最底下开始，边往上走，边往左走。

2、修改单点呢？

　　从最底下开始，边往上走，边往下走。

LA2191:

题目链接：https://vjudge.net/contest/147973#problem/A

题意：

先给出一个数组，然后有两个操作

S x y 把第x个数改成y

M x y计算x~y个数的和

Source Code:

 #include <bits/stdc++.h>

 using namespace std;

 inline int lowbit(int x)
 {
     return x&-x;
 }

 struct FenwickTree
 {
     int n;
     vector<int> C;

     void resize(int n)
     {
         this->n = n;
         C.resize(n+);
     }
     void clear()
     {
         fill(C.begin(), C.end(), );
     }

     // 计算A[1]+A[2]+...+A[x] (x<=n)
     int sum(int x)
     {
         int ret = ;
         while(x > )
         {
             ret += C[x];
             x -= lowbit(x);
         }
         return ret;
     }

     // A[x] += d (1<=x<=n)
     void add(int x, int d)
     {
         while(x <= n)
         {
             C[x] += d;
             x += lowbit(x);
         }
     }
 };

 FenwickTree f;
 const int maxn = +;
 int a[maxn];

 int main()
 {
    // freopen("in.txt","r",stdin);
     int n;
     int cases = ;
     while(scanf("%d",&n),n)
     {
         if(cases>) puts("");
         printf("Case %d:\n",++cases);
         f.resize(n);
         f.clear();
         for(int i=; i<=n; i++)
         {
             scanf("%d",&a[i]);
             f.add(i,a[i]);
         }

         char op[];
         while(scanf("%s",op)!=EOF)
         {
             if(!strcmp(op,"END"))
                 break;
             if(op[]=='M')
             {
                 int x,y;
                 scanf("%d%d",&x,&y);
                 printf("%d\n",f.sum(y)-f.sum(x-));
             }
             if(op[]=='S')
             {
                 int x,y;
                 scanf("%d%d",&x,&y);
                 int add = y - a[x];
                 a[x] = y;
                 f.add(x,add);
             }
         }
     }

     return ;
 }

LA5902:

题目链接：https://vjudge.net/contest/147973#problem/B

题意：

XXX喜欢看电影，他有好多好多的影碟，每个影碟都有个独立的编号。开始是从下往上影碟的顺序是n~1，他每次拿出影碟的时候，你需要输出压在该影碟上的有几个。（拿出后其他影碟顺序不变）看完影碟后，XXX会把影碟放在最上面。

分析：

把每个影碟放到一个考后的位置，这个位置有影碟，那么这里就是 1，否则是 0 ，每次询问，就是这个影碟所在的位置之前的前缀和，

把他放到前面去，当前位置置为 0 ，top 的位置 加 1，注意要记录每个影碟的所在位置。

Source Code：

 #include <bits/stdc++.h>

 using namespace std;

 inline int lowbit(int x)
 {
     return x&-x;
 }

 struct FenwickTree
 {
     int n;
     vector<int> C;

     void resize(int n)
     {
         this->n = n;
         C.resize(n);
     }
     void clear()
     {
         fill(C.begin(), C.end(), );
     }

     // 计算A[1]+A[2]+...+A[x] (x<=n)
     int sum(int x)
     {
         int ret = ;
         while(x > )
         {
             ret += C[x];
             x -= lowbit(x);
         }
         return ret;
     }

     // A[x] += d (1<=x<=n)
     void add(int x, int d)
     {
         while(x <= n)
         {
             C[x] += d;
             x += lowbit(x);
         }
     }
 };

 FenwickTree f;
 const int maxn = +;
 int pos[maxn];

 int main()
 {
     //freopen("in.txt","r",stdin);
     //freopen("out.txt","w",stdout);
     int t;
     scanf("%d",&t);

     while(t--)
     {
         int n,q;
         scanf("%d%d",&n,&q);
         f.resize(maxn*);
         f.clear();

         for(int i=; i<=n; i++)
         {
             f.add(maxn+i,);
             pos[i] = maxn+i;
         }

         int top = maxn;
         while(q--)
         {
             int x;
             scanf("%d",&x);
             int tmp = pos[x];
             if(q!=)
                 printf("%d ",f.sum(tmp-));
             else printf("%d",f.sum(tmp-));
             f.add(tmp,-);
             f.add(top--,);
             pos[x] = top + ;
         }
         puts("");
     }
     return ;
 }

LA4329

题目链接：https://icpcarchive.ecs.baylor.edu/index.php?option=com_onlinejudge&Itemid=8&category=26&page=show_problem&problem=2330

题意：

一条大街上住着n个乒乓球爱好者，经常组织比赛。每个人都有一个技能值ai，每场比赛需要3个人：两名选手和一名裁判。规定裁判位置必须在两个选手的中间，而且技能值也必须在两个选手的中间，问一共能组织多少种比赛。

分析：

和上题类似，每个技能值有的话为 1 ，否则为 0 ，每一个点都可以做裁判，那么他能组织多少场比赛？

a₁~a_i-1 有 ci个比 ai 小，a_i+1~a_n有di个比他小，乘法加法原理，ci(n-i-di) + di(i-ci-1)。

 #include <bits/stdc++.h>

 using namespace std;

 inline int lowbit(int x) {
     return x&-x;
 }

 struct FenwickTree {
     int n;
     vector<int> C;

     void resize(int n) {
         this->n = n;
         C.resize(n);
     }

     void clear() {
         fill(C.begin(),C.end(),);
     }

     //计算A[1] + A[2] + ... +A[n]
     int sum(int x) {
         int ret = ;
         while(x>) {
             ret +=C[x];
             x -=lowbit(x);
         }
         return ret;
     }

     // A[x] +=d;
     void add(int x,int d) {
         while(x<=n) {
             C[x] +=d;
             x +=lowbit(x);
         }
     }
 };

 const int maxn =  + ;
 int n;
 int a[maxn];
 FenwickTree f;
 int c[maxn],d[maxn];

 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--)
     {
         int maxa  = ;
         scanf("%d",&n);
         for(int i=;i<=n;i++) {
             scanf("%d",&a[i]);
             maxa = max(maxa,a[i]);
         }

         f.resize(maxa);
         f.clear();

         for(int i=;i<=n;i++) {
             f.add(a[i],);
             c[i] = f.sum(a[i]-);
         }

         f.clear();
         for(int i=n;i>=;i--) {
             f.add(a[i],);
             d[i] = f.sum(a[i]-);
         }

         long long ans = ;
         for(int i=;i<=n;i++) {
             ans +=(long long)c[i]*(n-i-d[i]) + (long long)(i-c[i]-)*d[i];
         }
         printf("%lld\n",ans);
     }

     return ;
 }