POJ-3565 Ants---KM算法+slack优化

题目链接：

https://vjudge.net/problem/POJ-3565

题目大意：

在坐标系中有N只蚂蚁，N棵苹果树，给你蚂蚁和苹果树的坐标。让每只蚂蚁去一棵苹果树，

一棵苹果树对应一只蚂蚁。这样就有N条直线路线，问：怎样分配，才能使总路程和最小，且

N条线不相交。

解题思路：

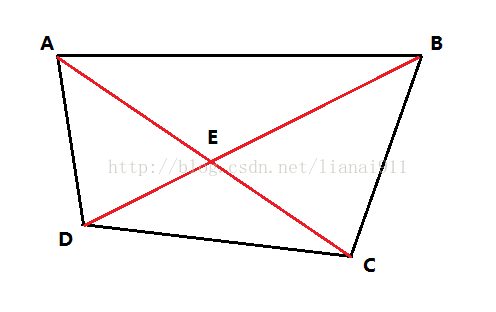
用一个图来说明思路。

假设A、B为蚂蚁，C、D为苹果树。则存在两种匹配：第一种是AD、BC，第二种是AC、BD。

根据三角形不等式AD+BC < AC+BD，最后得到很重要的一个性质——满足总路程之和最小

的方案一定不相交。现在来构建二分图，一边为蚂蚁，另一边为苹果树，以距离为边权值，题

目就变为了求带权二分图最小权和的最佳匹配。反向来思考，将距离乘以-1取负值建图，那么

就变为了求带权二分图最大权和的最佳匹配。直接用KM算法来做。

注意：用double，用slack数组优化（比全局变量快很多，网上看到说对于完全图优化会很快，用全局变量代替slack数组就超时）

 #include<iostream>
 #include<vector>
 #include<cstring>
 #include<queue>
 #include<cmath>
 #include<cstdio>
 using namespace std;
 const int maxn =  + ;
 const int INF = 0x3f3f3f3f;
 double Map[maxn][maxn];
 double wx[maxn], wy[maxn];//顶标值
 int cx[maxn], cy[maxn];
 //cx[i]表示与x部的点i匹配的y部的点的编号
 //cy[i]表示与y部的点i匹配的x部的点的编号
 bool visx[maxn], visy[maxn];//标记y部的点是否加入增广路
 int cntx, cnty;//x部点的数目和y部点的数目
 double minz;//边权顶标最小值
 double slack[maxn];
 bool dfs(int u)//进入的都是X部的点
 {
     visx[u] = ;
     for(int v = ; v <= cnty; v++)
     {
         if(!visy[v] && Map[u][v] != INF)
         {
             double t = wx[u] + wy[v] - Map[u][v];
             if(fabs(t) < 1e-)
             {
                 visy[v] = ;
                 if(cy[v] == - || dfs(cy[v]))
                 {
                     cx[u] = v;
                     cy[v] = u;
                     return true;
                 }
             }
             else if(slack[v] > t)
                 slack[v] = t;
         }
     }
     return false;
 }

 void KM()
 {
     memset(cx, -, sizeof(cx));
     memset(cy, -, sizeof(cy));
     memset(wy, , sizeof(wy));
     for(int i = ; i <= cntx; i++)wx[i] = -1.0 * INF;
     for(int i = ; i <= cntx; i++)
     {
         for(int j = ; j <= cnty; j++)
         {
             wx[i] = max(wx[i], Map[i][j]);
         }
     }
     for(int i = ; i <= cntx; i++)
     {
         for(int j = ; j <= cnty; j++)
             slack[j] = INF;
         while()
         {
             minz = 1.0 * INF;
             memset(visx, , sizeof(visx));
             memset(visy, , sizeof(visy));
             if(dfs(i))break;
             double d = INF;
             for(int i = ; i <= cnty; i++)
                 if(!visy[i] && d > slack[i])
                 d = slack[i];
             for(int j = ; j <= cntx; j++)
                 if(visx[j])wx[j] -= d;
             for(int j = ; j <= cnty; j++)
                 if(visy[j])wy[j] += d;
                 else slack[j] -= d;
         }
     }
     for(int i = ; i <= cntx; i++)
         printf("%d\n", cx[i]);
 }
 struct node
 {
     double x, y;
 }a[maxn], b[maxn];
 double dis(node a, node b)
 {
     return -sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y));
 }
 int main()
 {
     int n;
     scanf("%d", &n);
     cntx = cnty = n;
     for(int i = ; i <= n; i++)scanf("%lf%lf", &a[i].x, &a[i].y);
     for(int i = ; i <= n; i++)scanf("%lf%lf", &b[i].x, &b[i].y);
     for(int i = ; i <= n; i++)
     {
         for(int j = ; j <= n; j++)
             Map[i][j] = dis(a[i], b[j]);
     }
     KM();
 }