【志银】NYOJ《题目860》又见01背包
题目链接:http://acm.nyist.net/JudgeOnline/problem.php?pid=860
方法一:不用滚动数组(方法二为用滚动数组,为方法一的简化)
动态规划分析:最少要拿总价值一定,求所拿的最小质量(根据"最大能拿总重量一定,求能拿的最大价值"原理推导)
(PS:为了更好的理解,先不用滚动数组,直接开了两个数组,第一个数组用来储存最少要拿总价值为j时所拿的最小质量,第二个数组用来储存第一个的改变前状态)
例:
最大总质量sw = 5,物品数量n = 4;
1 2 3 4 <-第i个物品
w[] = {2, 1, 3, 2} //重量
v[] = {3, 2, 4, 2} //价值
最大总质量sw = 5,最大总价值sv = 11,物品数量n = 4;
分析打表结果如下:

#include<iostream>
using namespace std;
int main() {
int n, sw, sv, v[], w[], m[], b[]; //n为物品数量,sw为总重量,sv为总价值
while(cin >> n >> sw) { //m[j]为最少要拿总价值为j时所拿的最小质量
sv = ; //b[i]用来储存m[i]的上一个状态,如果用滚动数组方法就可以去掉b[]数组
for(int i = ; i <= n; i++) {
cin >> w[i] >> v[i];
sv += v[i];
}
for(int j = ; j <= ; j++) {
m[j] = ; //初始化为题目范围内最大值
b[j] = m[j];
}
m[] = b[] = ;
for(int i = ; i <= n; i++) {
for(int j = ; j <= sv; j++) {
if(j >= v[i]) m[j] = min(b[j], b[j-v[i]]+w[i]);
else m[j] = min(b[j], w[i]);
}
for(int j = ; j <= sv; j++) {
b[j] = m[j];
//b[j] > 1000000000 ? cout << "+ " : cout << b[j] << " "; //去掉这两行注释可打表结果
}
//cout << endl;
}
int big = ; //从价值为1开始找所有能拿到的价值
while(big <= sv && b[big] <= sw) big++;
cout << big- << endl;
}
}
代码实现(点击展开)
方法二:用滚动数组(方法一的简化)
原理:利用方法一的表格,按照价值j倒序计算表中的值
#include<iostream>
using namespace std;
int main() {
int n, sw, sv, v[], w[], m[]; //n为物品数量,sw为总重量,sv为总价值
while(cin >> n >> sw) { //m[j]为最少要拿总价值为j时所拿的最小质量
sv = ;
for(int i = ; i <= n; i++) { cin >> w[i] >> v[i]; sv += v[i]; }
for(int j = ; j <= ; j++) m[j] = ; //初始化为题目范围内最大值
for(int i = ; i <= n; i++) {
for(int j = sv; j >= ; j--) {
if(j >= v[i]) m[j] = min(m[j], m[j-v[i]]+w[i]);
else m[j] = min(m[j], w[i]);
//m[j] > 1000000000 ? cout << "+ " : cout << m[j] << " "; //去掉这两行注释可打表结果
}
//cout << endl;
}
int big = ; //从价值为1开始找所有能拿到的价值
while(big <= sv && m[big] <= sw) big++;
cout << big- << endl;
}
}
代码实现(点击展开)
开始写于:2016.5.20 ----志银
【志银】NYOJ《题目860》又见01背包的更多相关文章
- NYOJ:题目860 又见01背包
题目链接:http://acm.nyist.net/JudgeOnline/problem.php?pid=860 方法一:不用滚动数组(方法二为用滚动数组,为方法一的简化) 动态规划分析:最少要拿总 ...
- [NYOJ 860] 又见01背包
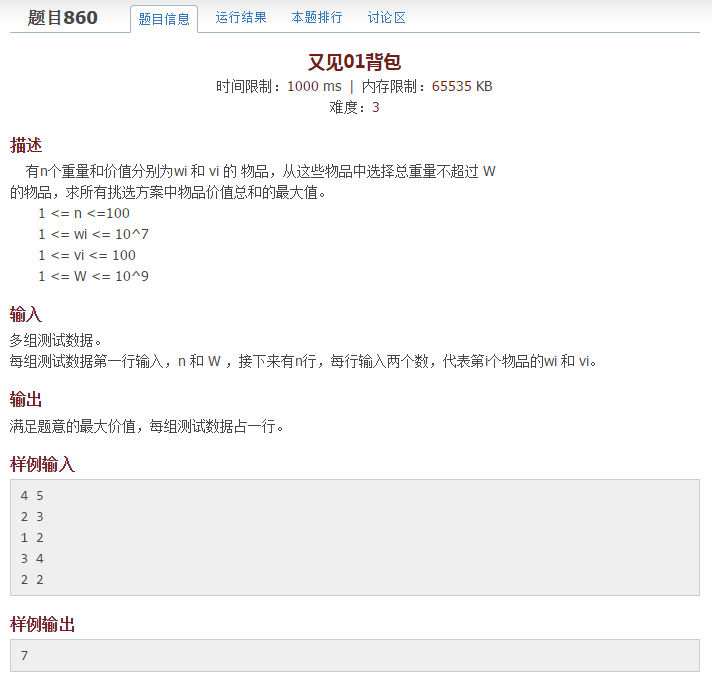
又见01背包 时间限制:1000 ms | 内存限制:65535 KB 难度:3 描述 有n个重量和价值分别为wi 和 vi 的 物品,从这些物品中选择总重量不超过 W 的物品,求所 ...
- NYIST 860 又见01背包
又见01背包时间限制:1000 ms | 内存限制:65535 KB难度:3 描述 有n个重量和价值分别为wi 和 vi 的 物品,从这些物品中选择总重量不超过 W 的物品,求所有挑选方案中物品价值总 ...
- nyoj860 又见01背包(背包变形)
题目860 pid=860" style="text-decoration:none; color:rgb(55,119,188)">题目信息 执行结果 本题排行 ...
- NYOJ--860 又见01背包(01背包)
题目http://acm.nyist.net/JudgeOnline/problem.php?pid=860 分析:题目和普通的01背包问题一样,但是唯一不同的是数据的特殊性. 如果10^9根本就开辟 ...
- HDU 2639 骨头收集者 II【01背包 】+【第K优决策】
题目链接:https://vjudge.net/contest/103424#problem/H 题目大意:与01背包模板题类似,只不过要我们求第K个最大的总价值. 解题分析: 其基本思想是将每个状态 ...
- hdu2126 类01背包(三维数组的二维空间优化)
题目描述: 对于给出的n个物品,每个物品有一个价格p[i],你有m元钱,求最多能买的物品个数,以及有多少种不同的方案 题目分析: 类似01背包的题目,一般的01背包问题我们遇到的是求n个物品,有m的容 ...
- Course Selection System ZOJ - 3956 01背包+思维
Course Selection System ZOJ - 3956 这个题目居然是一个01背包,我觉得好难想啊,根本就没有想到. 这个题目把题目给的转化为 ans = a*a-a*b-b*b 这个 ...
- 【志银】NYOJ《题目524》A-B Problem
题目链接:http://acm.nyist.net/JudgeOnline/problem.php?pid=860 My思路: 先用两个字符串储存这两个实数,然后再用另外两个字符串储存去掉符号和前后多 ...
随机推荐
- 【转】你是不是也被Android Private Libraries、Referenced Libraries、android Dependency搞晕了~~
一.v4.v7.v13的作用和用法 1.Android Support V4, V7, V13是什么? 本质上就是三个java library. 2.为什么要有support库? 是为了解决软件的 ...
- PMVS论文随笔(1)
博客园排版系统真的比较挫,可以访问我的github.io阅读 关于Unit的概念 在pmvs的源代码中,有一个函数是getUnit ,其函数如下(在PMVS2的windows版本代码,optim.cc ...
- Vuex基础-Mutation
借助官网的一张图,更改 Vuex 的 store 中的状态的唯一方法是提交 mutation.不可以直接对其进行赋值改变.需要注意的是,mutations只能做一些同步的操作. 代码结构: ...
- 基于asp.net MVC 的服务器和客户端的交互(一)
架构思想 三层架构 提出了一种基于ASP.NET开发方式的三层架构的Web应用系统构造思想.其基本内容是:将面向对象的UML建模与Web应用系统开发 相结合,将整个系统分成适合ASP.NET开发方式的 ...
- Latex 使用笔记,取消目录
不使用标准模板(如ieee或者acm的模板)的前提下: \usepackage{hyperref} \hypersetup{bookmarks={false}} 或者 \usepackage[book ...
- mysql的jdbc.url携带allowMultiQueries=true参数的作用及其原理
如下配置 jdbc.url=jdbc:mysql://127.0.0.1:3306/chubb_2?autoReconnect=true&useUnicode=true&charact ...
- javaScript的闭包 js变量作用域
js的闭包 js的变量作用域: var a=90; //定义一个全局变量 function test(){ a=123; //使用外层的 a变量 } test(); document.write(&q ...
- PHP小练习题
前几天在百度知道里面看到有位网友询问如何制作一下的小程序:用php语言设计一个小程序,计算今天到达下月的天数.全部输出这些天数,并使得每天的日期以三种颜色循环显示,设置三个表单,让用户选择字体颜色,然 ...
- python基础之列表、元组和字典
列表 列表定义:[]内以逗号分隔,按照索引,存放各种数据类型,每个位置代表一个元素 特性: 1.可存放多个值 2.可修改指定索引位置对应的值,可变 3.按照从左到右的顺序定义列表元素,下标从0开始顺序 ...
- Git-补丁文件交互
版本库间的交互是通过git push和/或git pull命令实现的,这是Git最主要的交互模式,但并不是全部.使用补丁文件是另外一种交互方式,适用于参与者众多的大型项目进行分布式开发. 创建补丁 G ...
